Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T04:53:18.747Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent Rayleigh–Bénard convection in spherical shells

Published online by Cambridge University Press:  10 August 2015

Thomas Gastine ,
Johannes Wicht  and
Jonathan M. Aurnou
Thomas Gastine*
Affiliation:
Max Planck Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
Johannes Wicht
Affiliation:
Max Planck Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
Jonathan M. Aurnou
Affiliation:
Department of Earth, Planetary and Space Sciences, University of California, Los Angeles, CA 90095-1567, USA
*
†Email address for correspondence: gastine@mps.mpg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

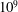We simulate numerically Boussinesq convection in non-rotating spherical shells for a fluid with a Prandtl number of unity and for Rayleigh numbers up to $10^{9}$. In this geometry, curvature and radial variations of the gravitational acceleration yield asymmetric boundary layers. A systematic parameter study for various radius ratios (from 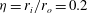${\it\eta}=r_{i}/r_{o}=0.2$ to 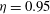${\it\eta}=0.95$) and gravity profiles allows us to explore the dependence of the asymmetry on these parameters. We find that the average plume spacing is comparable between the spherical inner and outer bounding surfaces. An estimate of the average plume separation allows us to accurately predict the boundary layer asymmetry for the various spherical shell configurations explored here. The mean temperature and horizontal velocity profiles are in good agreement with classical Prandtl–Blasius laminar boundary layer profiles, provided the boundary layers are analysed in a dynamical frame that fluctuates with the local and instantaneous boundary layer thicknesses. The scaling properties of the Nusselt and Reynolds numbers are investigated by separating the bulk and boundary layer contributions to the thermal and viscous dissipation rates using numerical models with 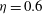${\it\eta}=0.6$ and with gravity proportional to 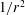$1/r^{2}$. We show that our spherical models are consistent with the predictions of Grossmann & Lohse’s (J. Fluid Mech., vol. 407, 2000, pp. 27–56) theory and that 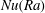$\mathit{Nu}(\mathit{Ra})$ and 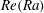$\mathit{Re}(\mathit{Ra})$ scalings are in good agreement with plane layer results.

JFM classification

Boundary Layers: Boundary Layers Geophysical and Geological Flows: Geophysical and Geological Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 721 - 764
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Amati, G., Koal, K., Massaioli, F., Sreenivasan, K. R. & Verzicco, R. 2005 Turbulent thermal convection at high Rayleigh numbers for a Boussinesq fluid of constant Prandtl number. Phys. Fluids 17 (12), 121701.CrossRefGoogle Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
Bercovici, D., Schubert, G. & Glatzmaier, G. A. 1992 Three-dimensional convection of an infinite-Prandtl-number compressible fluid in a basally heated spherical shell. J. Fluid Mech. 239, 683–719.CrossRefGoogle Scholar
Bercovici, D., Schubert, G., Glatzmaier, G. A. & Zebib, A. 1989 Three-dimensional thermal convection in a spherical shell. J. Fluid Mech. 206, 75–104.CrossRefGoogle Scholar
Blasius, H. 1908 Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 56, 1–37.Google Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69 (2), 026302.CrossRefGoogle ScholarPubMed
Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard turbulence. Phys. Fluids 17 (5), 055107.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Kadanoff, L., Libchaber, A. & Heslot, F. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chavanne, X., Chillà, F., Castaing, B., Hébral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648–3651.CrossRefGoogle Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201, 1–17.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.CrossRefGoogle ScholarPubMed
Ching, E. S., Guo, H., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Extraction of plumes in turbulent thermal convection. Phys. Rev. Lett. 93 (12), 124501.CrossRefGoogle ScholarPubMed
Choblet, G. 2012 On the scaling of heat transfer for mixed heating convection in a spherical shell. Phys. Earth Planet. Inter. 206, 31–42.CrossRefGoogle Scholar
Christensen, U. R. & Wicht, J. 2007 Numerical dynamo simulations. In Core Dynamics (ed. Olson, P.), pp. 245–282. Elsevier.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166, 97–114.CrossRefGoogle Scholar
Christensen, U.  R., Aubert, J., Cardin, P., Dormy, E., Gibbons, S., Glatzmaier, G. A., Grote, E., Honkura, Y., Jones, C., Kono, M., Matsushima, M., Sakuraba, A., Takahashi, F., Tilgner, A., Wicht, J. & Zhang, K. 2001 A numerical dynamo benchmark. Phys. Earth Planet. Inter. 128, 25–34.CrossRefGoogle Scholar
Deschamps, F., Tackley, P. J. & Nakagawa, T. 2010 Temperature and heat flux scalings for isoviscous thermal convection in spherical geometry. Geophys. J. Intl 182, 137–154.Google Scholar
Feldman, Y. & Colonius, T. 2013 On a transitional and turbulent natural convection in spherical shells. Intl J. Heat Mass Transfer 64 (0), 514–525.CrossRefGoogle Scholar
Feudel, F., Bergemann, K., Tuckerman, L. S., Egbers, C., Futterer, B., Gellert, M. & Hollerbach, R. 2011 Convection patterns in a spherical fluid shell. Phys. Rev. E 83 (4), 046304.CrossRefGoogle Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
Futterer, B., Egbers, C., Dahley, N., Koch, S. & Jehring, L. 2010 First identification of sub- and supercritical convection patterns from ‘GeoFlow’, the geophysical flow simulation experiment integrated in Fluid Science Laboratory. Acta Astronaut. 66 (1–2), 193–200.CrossRefGoogle Scholar
Futterer, B., Krebs, A., Plesa, A.-C., Zaussinger, F., Hollerbach, R., Breuer, D. & Egbers, C. 2013 Sheet-like and plume-like thermal flow in a spherical convection experiment performed under microgravity. J. Fluid Mech. 735, 647–683.CrossRefGoogle Scholar
Gastine, T. & Wicht, J. 2012 Effects of compressibility on driving zonal flow in gas giants. Icarus 219, 428–442.CrossRefGoogle Scholar
Gastine, T., Wicht, J. & Aurnou, J. 2013 Zonal flow regimes in rotating spherical shells: an application to giant planets. Icarus 225, 156–172.CrossRefGoogle Scholar
Gilman, P. A. & Glatzmaier, G. A. 1981 Compressible convection in a rotating spherical shell – I – Anelastic equations. Astrophys. J. Suppl. 45, 335–349.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.CrossRefGoogle Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bénard convection. J. Comput. Phys. 49, 241–264.CrossRefGoogle Scholar
Gunasegarane, G. S. & Puthenveettil, B. A. 2014 Dynamics of line plumes on horizontal surfaces in turbulent convection. J. Fluid Mech. 749, 37–78.CrossRefGoogle Scholar
Hart, J. E., Glatzmaier, G. A. & Toomre, J. 1986 Space-laboratory and numerical simulations of thermal convection in a rotating hemispherical shell with radial gravity. J. Fluid Mech. 173, 519–544.CrossRefGoogle Scholar
Jarvis, G. T. 1993 Effects of curvature on two-dimensional models of mantle convection – cylindrical polar coordinates. J. Geophys. Res. 98, 4477–4485.CrossRefGoogle Scholar
Jarvis, G. T., Glatzmaier, G. A. & Vangelov, V. I. 1995 Effects of curvature, aspect ratio and plan form in two- and three-dimensional spherical models of thermal convection. Geophys. Astrophys. Fluid Dyn. 79, 147–171.CrossRefGoogle Scholar
Jones, C. A., Boronski, P., Brun, A. S., Glatzmaier, G. A., Gastine, T., Miesch, M. S. & Wicht, J. 2011 Anelastic convection-driven dynamo benchmarks. Icarus 216, 120–135.CrossRefGoogle Scholar
Kerr, R. M. & Herring, J. R. 2000 Prandtl number dependence of Nusselt number in direct numerical simulations. J. Fluid Mech. 419, 325–344.CrossRefGoogle Scholar
King, E. M., Soderlund, K. M., Christensen, U. R., Wicht, J. & Aurnou, J. M. 2010 Convective heat transfer in planetary dynamo models. Geochem. Geophys. Geosyst. 11, Q06016.CrossRefGoogle Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.CrossRefGoogle Scholar
King, E. M., Stellmach, S. & Buffett, B. 2013 Scaling behaviour in Rayleigh–Bénard convection with and without rotation. J. Fluid Mech. 717, 449–471.CrossRefGoogle Scholar
Lakkaraju, R., Stevens, R. J. A. M., Verzicco, R., Grossmann, S., Prosperetti, A., Sun, C. & Lohse, D. 2012 Spatial distribution of heat flux and fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 86 (5), 056315.CrossRefGoogle ScholarPubMed
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65 (6), 066306.CrossRefGoogle ScholarPubMed
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992 Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 68, 1515–1518.CrossRefGoogle ScholarPubMed
Liu, Y. & Ecke, R. E. 2011 Local temperature measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 84 (1), 016311.CrossRefGoogle ScholarPubMed
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
O’Farrell, K. A., Lowman, J. P. & Bunge, H.-P. 2013 Comparison of spherical-shell and plane-layer mantle convection thermal structure in viscously stratified models with mixed-mode heating: implications for the incorporation of temperature-dependent parameters. Geophys. J. Intl 192, 456–472.CrossRefGoogle Scholar
Parmentier, E. M. & Sotin, C. 2000 Three-dimensional numerical experiments on thermal convection in a very viscous fluid: implications for the dynamics of a thermal boundary layer at high Rayleigh number. Phys. Fluids 12, 609–617.CrossRefGoogle Scholar
Petschel, K., Stellmach, S., Wilczek, M., Lülff, J. & Hansen, U. 2013 Dissipation layers in Rayleigh–Bénard convection: a unifying view. Phys. Rev. Lett. 110 (11), 114502.CrossRefGoogle ScholarPubMed
Prandtl, L. 1905 Verhandlungen des III. Int. Math. Kongr., Heidelberg, 1904. pp. 484–491. Teubner.Google Scholar
Puthenveettil, B. A. & Arakeri, J. H. 2005 Plume structure in high-Rayleigh-number convection. J. Fluid Mech. 542, 217–249.CrossRefGoogle Scholar
Puthenveettil, B. A., Gunasegarane, G. S., Agrawal, Y. K., Schmeling, D., Bosbach, J. & Arakeri, J. H. 2011 Length of near-wall plumes in turbulent convection. J. Fluid Mech. 685, 335–364.CrossRefGoogle Scholar
du Puits, R., Resagk, C. & Thess, A. 2013 Thermal boundary layers in turbulent Rayleigh–Bénard convection at aspect ratios between 1 and 9. New J. Phys. 15 (1), 013040.CrossRefGoogle Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the Ultimate Regime of convection. New J. Phys. 12 (8), 085014.CrossRefGoogle Scholar
Rotem, Z. & Claassen, L. 1969 Natural convection above unconfined horizontal surfaces. J. Fluid Mech. 39, 173–192.CrossRefGoogle Scholar
Scanlan, J. A., Bishop, E. H. & Powe, R. E. 1970 Natural convection heat transfer between concentric spheres. Intl J. Heat Mass Transfer 13 (12), 1857–1872.CrossRefGoogle Scholar
Schaeffer, N. 2013 Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations. Geochem. Geophys. Geosyst. 14, 751–758.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory. Springer.CrossRefGoogle Scholar
Shahnas, H. M., Lowman, J. P., Jarvis, G. T. & Bunge, H.-P. 2008 Convection in a spherical shell heated by an isothermal core and internal sources: implications for the thermal state of planetary mantles. Phys. Earth Planet. Inter. 168, 6–15.CrossRefGoogle Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.CrossRefGoogle Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E. S. C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114 (11), 114302.CrossRefGoogle ScholarPubMed
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.CrossRefGoogle Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.CrossRefGoogle Scholar
Shishkina, O. & Wagner, C. 2005 Analysis of thermal dissipation rates in turbulent Rayleigh Bénard convection. J. Fluid Mech. 546, 51–60.CrossRefGoogle Scholar
Shishkina, O. & Wagner, C. 2008 Analysis of sheet-like thermal plumes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 599, 383–404.CrossRefGoogle Scholar
Shraiman, B.  I. & Siggia, E.  D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
Sotin, C. & Labrosse, S. 1999 Three-dimensional thermal convection in an iso-viscous, infinite Prandtl number fluid heated from within and from below: applications to the transfer of heat through planetary mantles. Phys. Earth Planet. Inter. 112, 171–190.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.CrossRefGoogle Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85 (2), 027301.CrossRefGoogle Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Tilgner, A. 1996 High-Rayleigh-number convection in spherical shells. Phys. Rev. E 53, 4847–4851.CrossRefGoogle ScholarPubMed
Tilgner, A. & Busse, F. H. 1997 Finite-amplitude convection in rotating spherical fluid shells. J. Fluid Mech. 332, 359–376.CrossRefGoogle Scholar
Vangelov, V. I. & Jarvis, G. T. 1994 Geometrical effects of curvature in axisymmetric spherical models of mantle convection. J. Geophys. Res. 99, 9345–9358.CrossRefGoogle Scholar
Verzicco, R. 2003 Turbulent thermal convection in a closed domain: viscous boundary layer and mean flow effects. Eur. Phys. J. B 35, 133–141.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.CrossRefGoogle Scholar
Vipin, K. & Puthenveettil, B. A.2013 Identification of coherent structures on the horizontal plate in turbulent convection. In Proceedings of the 8th World conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics ExHFT.Google Scholar
Wicht, J. 2002 Inner-core conductivity in numerical dynamo simulations. Phys. Earth Planet. Inter. 132, 281–302.CrossRefGoogle Scholar
Wolstencroft, M., Davies, J.  H. & Davies, D.  R. 2009 Nusselt-Rayleigh number scaling for spherical shell Earth mantle simulation up to a Rayleigh number of $10^{9}$ . Phys. Earth Planet. Inter. 176, 132–141.CrossRefGoogle Scholar
Wu, X.-Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.CrossRefGoogle ScholarPubMed
Xu, X., Bajaj, K. M. S. & Ahlers, G. 2000 Heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 84, 4357–4360.CrossRefGoogle ScholarPubMed
Zebib, A., Schubert, G. & Straus, J. M. 1980 Infinite Prandtl number thermal convection in a spherical shell. J. Fluid Mech. 97, 257–277.CrossRefGoogle Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9, 1034–1042.CrossRefGoogle Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, S.-Q. & Xia, K.-Q. 2002 Plume statistics in thermal turbulence: mixing of an active scalar. Phys. Rev. Lett. 89 (18), 184502.CrossRefGoogle ScholarPubMed
Zhou, Q. & Xia, K.-Q. 2010a Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104 (10), 104301.CrossRefGoogle ScholarPubMed
Zhou, Q. & Xia, K.-Q. 2010b Physical and geometrical properties of thermal plumes in turbulent Rayleigh–Bénard convection. New J. Phys. 12 (7), 075006.Google Scholar