Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T09:57:13.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional partially ionized magnetohydrodynamic turbulence

Published online by Cambridge University Press:  11 August 2020

Santiago J. Benavides Open the ORCID record for Santiago J. Benavides [Opens in a new window]  and
Glenn R. Flierl
Santiago J. Benavides*
Affiliation:
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA02139, USA
Glenn R. Flierl
Affiliation:
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA02139, USA
*
†Email address for correspondence: santib@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

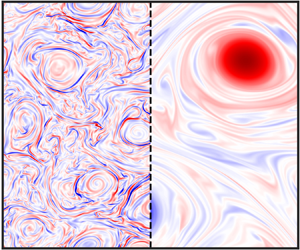
Ionization occurs in the upper atmospheres of hot Jupiters and in the interiors of gas giant planets, leading to magnetohydrodynamic (MHD) effects that couple the momentum and the magnetic field, thereby significantly altering the dynamics. In regions of moderate temperatures, the gas is only partially ionized, which also leads to interactions with neutral molecules. To explore the turbulent dynamics of these regions, we utilize partially ionized magnetohydrodynamics (PIMHD), a two-fluid model – one neutral and one ionized – coupled by a collision term proportional to the difference in velocities. Motivated by planetary settings where rotation constrains the large-scale motions to be mostly two-dimensional, we perform a suite of simulations to examine the parameter space of two-dimensional PIMHD turbulence and pay particular attention to collisions and their role in the dynamics, dissipation and energy exchange between the two species. We arrive at, and numerically confirm, an expression for the energy loss due to collisions in both the weakly and strongly collisional limits, and show that, in the latter limit, the neutral fluid couples to the ions and behaves as an MHD fluid. Finally, we discuss some implications of our findings to current understanding of gas giant planet atmospheres.

JFM classification

Geophysical and Geological Flows: Atmospheric flows MHD and Electrohydrodynamics: MHD turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 900 , 10 October 2020 , A28
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agrawal, R., Alexakis, A., Brachet, M. E. & Tuckerman, L. S. 2020 Turbulent cascade, bottleneck, and thermalized spectrum in hyperviscous flows. Phys. Rev. Fluids 5, 024601.CrossRefGoogle Scholar
Alexakis, A. & Biferale, L. 2018 Cascades and transitions in turbulent flows. Phys. Rep. 767–769, 1–101.CrossRefGoogle Scholar
Alexakis, A. & Brachet, M.-E. 2019 On the thermal equilibrium state of large-scale flows. J. Fluid Mech. 872, 594–625.CrossRefGoogle Scholar
Bagenal, F., Dowling, T. E. & McKinnon, W. B. 2006 Jupiter: The Planet, Satellites and Magnetosphere, vol. 1. Cambridge University Press.Google Scholar
Balbus, S. A. 2009 Magnetohydrodynamics of protostellar disks. arXiv:0906.0854.Google Scholar
Ballester, J. L., Alexeev, I., Collados, M., Downes, T., Pfaff, R. F., Gilbert, H., Khodachenko, M., Khomenko, E., Shaikhislamov, I. F., Soler, R., et al. 2018 Partially ionized plasmas in astrophysics. Space Sci. Rev. 214 (2), 58.CrossRefGoogle Scholar
Batygin, K., Stanley, S. & Stevenson, D. J. 2013 Magnetically controlled circulation on hot extrasolar planets. Astrophys. J. 776 (1), 53.CrossRefGoogle Scholar
Batygin, K. & Stevenson, D. J. 2010 Inflating hot Jupiters with ohmic dissipation. Astrophys. J. Lett. 714 (2), L238.CrossRefGoogle Scholar
Busse, F. H. 1976 A simple model of convection in the Jovian atmosphere. Icarus 29 (2), 255–260.CrossRefGoogle Scholar
Cao, H. & Stevenson, D. J. 2017 Zonal flow magnetic field interaction in the semi-conducting region of giant planets. Icarus 296, 59–72.CrossRefGoogle Scholar
Chai, J., Jansen, M. & Vallis, G. K. 2016 Equilibration of a baroclinic planetary atmosphere toward the limit of vanishing bottom friction. J. Atmos. Sci. 73 (8), 3249–3272.CrossRefGoogle Scholar
Chan, C.-K., Mitra, D. & Brandenburg, A. 2012 Dynamics of saturated energy condensation in two-dimensional turbulence. Phys. Rev. E 85, 036315.CrossRefGoogle ScholarPubMed
Cho, J. Y. K. & Polvani, L. M. 1996 The emergence of jets and vortices in freely evolving, shallow-water turbulence on a sphere. Phys. Fluids 8 (6), 1531–1552.CrossRefGoogle Scholar
Dietrich, W. & Jones, C. A. 2018 Anelastic spherical dynamos with radially variable electrical conductivity. Icarus 305, 15–32.CrossRefGoogle Scholar
Dowling, T. E. & Ingersoll, A. P. 1988 Potential vorticity and layer thickness variations in the flow around Jupiter's great red spot and white oval BC. J. Atmos. Sci. 45 (8), 1380–1396.2.0.CO;2>CrossRefGoogle Scholar
Dowling, T. E. & Ingersoll, A. P. 1989 Jupiter's great red spot as a shallow water system. J. Atmos. Sci. 46 (21), 3256–3278.2.0.CO;2>CrossRefGoogle Scholar
Draine, B. T. 1980 Interstellar shock waves with magnetic precursors. Astrophys. J. 241, 1021–1038.CrossRefGoogle Scholar
Draine, B. T. 1986 Multicomponent, reacting MHD flows. Mon. Not. R. Astron. Soc. 220 (1), 133–148.CrossRefGoogle Scholar
Duarte, L. D. V., Wicht, J. & Gastine, T. 2018 Physical conditions for Jupiter-like dynamo models. Icarus 299, 206–221.CrossRefGoogle Scholar
Falle, S. A. E. G. 2003 A numerical scheme for multifluid magnetohydrodynamics. Mon. Not. R. Astron. Soc. 344 (4), 1210–1218.CrossRefGoogle Scholar
French, M., Becker, A., Lorenzen, W., Nettelmann, N., Bethkenhagen, M., Wicht, J. & Redmer, R. 2012 Ab initio simulations for material properties along the Jupiter adiabat. Astrophys. J. Suppl. Ser. 202 (1), 5.CrossRefGoogle Scholar
Gallet, B. & Young, W. R. 2013 A two-dimensional vortex condensate at high Reynolds number. J. Fluid Mech. 715, 359–388.CrossRefGoogle Scholar
Gastine, T., Wicht, J., Duarte, L. D. V., Heimpel, M. & Becker, A. 2014 Explaining Jupiter's magnetic field and equatorial jet dynamics. Geophys. Res. Lett. 41 (15), 5410–5419.CrossRefGoogle Scholar
Glatzmaier, G. A. 2008 A note on ‘Constraints on deep-seated zonal winds inside Jupiter and Saturn’. Icarus 196 (2), 665–666.CrossRefGoogle Scholar
Glatzmaier, G. A., Evonuk, M. & Rogers, T. M. 2009 Differential rotation in giant planets maintained by density-stratified turbulent convection. Geophys. Astrophys. Fluid Dyn. 103 (1), 31–51.CrossRefGoogle Scholar
Gómez, D. O., Mininni, P. D. & Dmitruk, P. 2005 Parallel simulations in turbulent MHD. Phys. Scr. 2005 (T116), 123.CrossRefGoogle Scholar
Guillot, T. 2005 The interiors of giant planets: models and outstanding questions. Annu. Rev. Earth Planet. Sci. 33 (1), 493–530.CrossRefGoogle Scholar
Heimpel, M., Gastine, T. & Wicht, J. 2016 Simulation of deep-seated zonal jets and shallow vortices in gas giant atmospheres. Nat. Geosci. 9 (1), 19–23.CrossRefGoogle Scholar
Jones, C. A. 2014 A dynamo model of Jupiter's magnetic field. Icarus 241, 148–159.CrossRefGoogle Scholar
Jones, C. A., Boronski, P., Brun, A. S., Glatzmaier, G. A., Gastine, T., Miesch, M. S. & Wicht, J. 2011 Anelastic convection-driven dynamo benchmarks. Icarus 216 (1), 120–135.CrossRefGoogle Scholar
Kaspi, Y., Galanti, E., Hubbard, W. B., Stevenson, D. J., Bolton, S. J., Iess, L., Guillot, T., Bloxham, J., Connerney, J. E. P., Cao, H., et al. 2018 Jupiter's atmospheric jet streams extend thousands of kilometres deep. Nature 555, 223–226.CrossRefGoogle ScholarPubMed
Khodachenko, M. L., Arber, T. D., Rucker, H. O. & Hanslmeier, A. 2004 Collisional and viscous damping of MHD waves in partially ionized plasmas of the solar atmosphere. Astron. Astrophys. 422, 1073–1084.CrossRefGoogle Scholar
Khomenko, E. & Collados, M. 2012 Heating of the magnetized solar chromosphere by partial ionization effects. Astrophys. J. 747 (2), 87.CrossRefGoogle Scholar
Koll, D. D. B. & Komacek, T. D. 2018 Atmospheric circulations of hot Jupiters as planetary heat engines. Astrophys. J. 853 (2), 133.CrossRefGoogle Scholar
Koskinen, T. T., Yelle, R. V., Lavvas, P. & Cho, J. Y. K. 2014 Electrodynamics on extrasolar giant planets. Astrophys. J. 796 (1), 16.CrossRefGoogle Scholar
Lazarian, A., Vishniac, E. T. & Cho, J. 2004 Magnetic field structure and stochastic reconnection in a partially ionized gas. Astrophys. J. 603 (1), 180–197.CrossRefGoogle Scholar
Leake, J. E., DeVore, C. R., Thayer, J. P., Burns, A. G., Crowley, G., Gilbert, H. R., Huba, J. D., Krall, J., Linton, M. G., Lukin, V. S., et al. 2014 Ionized plasma and neutral gas coupling in the Sun's chromosphere and Earth's ionosphere/thermosphere. Space Sci. Rev. 184 (1–4), 107–172.CrossRefGoogle Scholar
Leake, J. E., Lukin, V. S. & Linton, M. G. 2013 Magnetic reconnection in a weakly ionized plasma. Phys. Plasmas 20 (6), 061202.CrossRefGoogle Scholar
Leake, J. E., Lukin, V. S., Linton, M. G. & Meier, E. T. 2012 Multi-fluid simulations of chromospheric magnetic reconnection in a weakly ionized reacting plasma. Astrophys. J. 760 (2), 109.CrossRefGoogle Scholar
Lian, Y. & Showman, A. P. 2008 Deep jets on gas-giant planets. Icarus 194 (2), 597–615.CrossRefGoogle Scholar
Lian, Y. & Showman, A. P. 2010 Generation of equatorial jets by large-scale latent heating on the giant planets. Icarus 207 (1), 373–393.CrossRefGoogle Scholar
Liu, J., Goldreich, P. M. & Stevenson, D. J. 2008 Constraints on deep-seated zonal winds inside Jupiter and Saturn. Icarus 196 (2), 653–664.CrossRefGoogle Scholar
Malyshkin, L. M. & Zweibel, E. G. 2011 Onset of fast magnetic reconnection in partially ionized gases. Astrophys. J. 739 (2), 1–12.CrossRefGoogle Scholar
Martínez-Sykora, J., De Pontieu, B., Hansteen, V. H., Rouppe van der Voort, L., Carlsson, M. & Pereira, T. M. D. 2017 On the generation of solar spicules and Alfvénic waves. Science 356 (6344), 1269–1272.CrossRefGoogle ScholarPubMed
Meier, E. T. 2011 Modeling plasmas with strong anisotropy, neutral fluid effects, and open boundaries. PhD thesis, University of Washington.Google Scholar
Meier, E. T. & Shumlak, U. 2012 A general nonlinear fluid model for reacting plasma-neutral mixtures. Phys. Plasmas 19 (7), 1–11.Google Scholar
Menou, K. 2012 Magnetic scaling laws for the atmospheres of hot giant exoplanets. Astrophys. J. 745 (2), 138.CrossRefGoogle Scholar
Meyer, C. D., Balsara, D. S., Burkhart, B. & Lazarian, A. 2014 Observational diagnostics for two-fluid turbulence in molecular clouds as suggested by simulations. Mon. Not. R. Astron. Soc. 439 (3), 2197–2210.CrossRefGoogle Scholar
Nakano, T. & Umebayashi, T. 1986 Dissipation of magnetic fields in very dense interstellar clouds – I. Formulation and conditions for efficient dissipation. Mon. Not. R. Astron. Soc. 218 (4), 663–684.CrossRefGoogle Scholar
Oishi, J. S. & Mac Low, M.-M. 2006 The inability of ambipolar diffusion to set a characteristic mass scale in molecular clouds. Astrophys. J. 638 (1), 281–285.CrossRefGoogle Scholar
O'Neill, M. E., Emanuel, K. A. & Flierl, G. R. 2015 Polar vortex formation in giant-planet atmospheres due to moist convection. Nat. Geosci. 8 (523), 523–526.CrossRefGoogle Scholar
O'Sullivan, S. & Downes, T. P. 2007 A three-dimensional numerical method for modelling weakly ionized plasmas. Mon. Not. R. Astron. Soc. 376 (4), 1648–1658.CrossRefGoogle Scholar
Pandey, B. P. & Wardle, M. 2008 Hall magnetohydrodynamics of partially ionized plasmas. Mon. Not. R. Astron. Soc. 385 (4), 2269–2278.CrossRefGoogle Scholar
Perna, R., Menou, K. & Rauscher, E. 2010 Magnetic drag on hot Jupiter atmospheric winds. Astrophys. J. 719 (2), 1421–1426.CrossRefGoogle Scholar
Rhines, P. B. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69 (3), 417–443.CrossRefGoogle Scholar
Rogers, T. M. & McElwaine, J. N. 2017 The hottest hot Jupiters may host atmospheric dynamos. Astrophys. J. Lett. 841 (2), L26.CrossRefGoogle Scholar
Rogers, T. M. & Showman, A. P. 2014 Magnetohydrodynamic simulations of the atmosphere of HD 209458B. Astrophys. J. Lett. 782 (1), L4.CrossRefGoogle Scholar
Schneider, T. & Liu, J. 2009 Formation of jets and equatorial superrotation on Jupiter. J. Atmos. Sci. 66 (3), 579–601.CrossRefGoogle Scholar
Scott, R. K. & Polvani, L. M. 2007 Forced-dissipative shallow–water turbulence on the sphere and the atmospheric circulation of the giant planets. J. Atmos. Sci. 64 (9), 3158–3176.CrossRefGoogle Scholar
Scott, R. K. & Polvani, L. M. 2008 Equatorial superrotation in shallow atmospheres. Geophys. Res. Lett. 35 (24), 1–5.CrossRefGoogle Scholar
Seshasayanan, K. & Alexakis, A. 2016 Critical behavior in the inverse to forward energy transition in two-dimensional magnetohydrodynamic flow. Phys. Rev. E 93 (1), 1–13.CrossRefGoogle ScholarPubMed
Seshasayanan, K., Benavides, S. J. & Alexakis, A. 2014 On the edge of an inverse cascade. Phys. Rev. E 90 (5), 1–5.CrossRefGoogle ScholarPubMed
Showman, A. P. 2007 Numerical simulations of forced shallow–water turbulence: effects of moist convection on the large-scale circulation of Jupiter and Saturn. J. Atmos. Sci. 64 (9), 3132–3157.CrossRefGoogle Scholar
Smith, M. D. & Mac Low, M.-M. 1997 The formation of C-shocks: structure and signatures. Astron. Astrophys. 326, 801–810.Google Scholar
Smith, P. D. & Sakai, J. I. 2008 Chromospheric magnetic reconnection: two-fluid simulations of coalescing current loops. Astron. Astrophys. 486, 569–575.CrossRefGoogle Scholar
Song, P. 2017 A model of the solar chromosphere: structure and internal circulation. Astrophys. J. 846 (2), 92.CrossRefGoogle Scholar
Stanley, S. & Glatzmaier, G. A. 2010 Dynamo models for planets other than Earth. Space Sci. Rev. 152 (1–4), 617–649.CrossRefGoogle Scholar
Tilley, D. A. & Balsara, D. S. 2010 Direct evidence for two-fluid effects in molecular clouds. Mon. Not. R. Astron. Soc. 406 (2), 1201–1207.Google Scholar
Tobias, S. M., Diamond, P. H. & Hughes, D. W. 2007 $\beta$-Plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. J. 667, 113–116.CrossRefGoogle Scholar
Vasyliunas, V. M. & Song, P. 2005 Meaning of ionospheric Joule heating. J. Geophys. Res. 110 (A2), 1–8.CrossRefGoogle Scholar
Warneford, E. S. & Dellar, P. J. 2014 Thermal shallow water models of geostrophic turbulence in Jovian atmospheres. Phys. Fluids 26 (1), 016603.CrossRefGoogle Scholar
Wicht, J. & Tilgner, A. 2010 Theory and modeling of planetary dynamos. Space Sci. Rev. 152 (1), 501–542.CrossRefGoogle Scholar
Xu, S. & Lazarian, A. 2017 Magnetohydrodynamic turbulence and turbulent dynamo in partially ionized plasma. New J. Phys. 19 (6), 065005.CrossRefGoogle Scholar
Xu, S., Yan, H. & Lazarian, A. 2016 Damping of magnetohydrodynamic turbulence in partially ionized plasma: implications for comsic ray propagation. Astrophys. J. 826 (2), 166.CrossRefGoogle Scholar
Zaghoo, M. 2018 Dynamic conductivity and partial ionization in dense fluid hydrogen. Phys. Rev. E 97, 043205.CrossRefGoogle ScholarPubMed
Zaqarashvili, T. V., Khodachenko, M. L. & Rucker, H. O. 2011 Magnetohydrodynamic waves in solar partially ionized plasmas: two-fluid approach. Astron. Astrophys. 529, A82.CrossRefGoogle Scholar