Published online by Cambridge University Press: 10 December 2019
The characteristics and dynamics of the uniform-momentum zones (UMZ) and UMZ interfaces in a fully developed turbulent pipe flow are studied using direct numerical simulation at  $Re_{\unicode[STIX]{x1D70F}}=500$. The multiple UMZs detected from the probability density functions of the instantaneous streamwise velocity following de Silva et al. (J. Fluid Mech., vol. 786, 2016, pp. 309–331) showed similarities to both turbulent channel and boundary layer flows (TBL): the hierarchical structural distribution of thinner UMZs with thinner interfaces nearer the wall, accompanied with sharper and larger jumps in the streamwise velocity at the UMZ interface. The conditional average results indicate that channel and pipe are very similar quantitatively whereas pipe and TBL display significant discrepancies. The innermost UMZs in pipe flow exhibit different behaviours to the other UMZs in pipes. The contortion of the UMZ interface representing the meandering of coherent motions with high- and low-momentum streaks is examined three-dimensionally. The meandering of UMZ in both two and three dimensions intensifies away from the wall and is always wavier in the azimuthal direction than the streamwise direction. The UMZs in the near-wall region capture the small-scale velocity fluctuation of the near-wall cycle and show asymmetric modulation of
$Re_{\unicode[STIX]{x1D70F}}=500$. The multiple UMZs detected from the probability density functions of the instantaneous streamwise velocity following de Silva et al. (J. Fluid Mech., vol. 786, 2016, pp. 309–331) showed similarities to both turbulent channel and boundary layer flows (TBL): the hierarchical structural distribution of thinner UMZs with thinner interfaces nearer the wall, accompanied with sharper and larger jumps in the streamwise velocity at the UMZ interface. The conditional average results indicate that channel and pipe are very similar quantitatively whereas pipe and TBL display significant discrepancies. The innermost UMZs in pipe flow exhibit different behaviours to the other UMZs in pipes. The contortion of the UMZ interface representing the meandering of coherent motions with high- and low-momentum streaks is examined three-dimensionally. The meandering of UMZ in both two and three dimensions intensifies away from the wall and is always wavier in the azimuthal direction than the streamwise direction. The UMZs in the near-wall region capture the small-scale velocity fluctuation of the near-wall cycle and show asymmetric modulation of  $Q2$ ejections over
$Q2$ ejections over  $Q4$ sweeps. The asymmetric modulation of ejections over sweeps decreases from the wall towards the pipe centre and the opposite trend of elevated
$Q4$ sweeps. The asymmetric modulation of ejections over sweeps decreases from the wall towards the pipe centre and the opposite trend of elevated  $Q4$ sweeps is observed for the innermost UMZs. Near the wall, the ejection regions are very spiky compared to the flat sweep regions whereas, in the pipe centre, the large-scale ejections are relatively flat and the sweep regions are spikier.
$Q4$ sweeps is observed for the innermost UMZs. Near the wall, the ejection regions are very spiky compared to the flat sweep regions whereas, in the pipe centre, the large-scale ejections are relatively flat and the sweep regions are spikier.
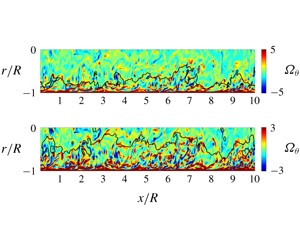
Time evolution of the attachment between UMZ interface defined at 0.9UCL (black line) and azimuthal vortices (coloured contour) in a fixed frame on a streamwise midplane of the pipe.
Time evolution of the attachment between UMZ interface defined at 0.9UCL (black line) and azimuthal vortices (coloured contour) in a moving frame on a streamwise midplane of the pipe. The frame moves downstream at the bulk mean velocity.