Published online by Cambridge University Press: 12 December 2017
Vorticity distributions in axisymmetric vortex rings produced by a piston–pipe apparatus are numerically studied over a range of Reynolds numbers, 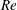 $Re$, and stroke-to-diameter ratios,
$Re$, and stroke-to-diameter ratios, 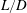 $L/D$. It is found that a state of advective balance, such that
$L/D$. It is found that a state of advective balance, such that 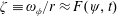 $\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}/r\approx F(\unicode[STIX]{x1D713},t)$, is achieved within the region (called the vortex ring bubble) enclosed by the dividing streamline. Here
$\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}/r\approx F(\unicode[STIX]{x1D713},t)$, is achieved within the region (called the vortex ring bubble) enclosed by the dividing streamline. Here 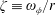 $\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}/r$ is the ratio of azimuthal vorticity to cylindrical radius, and
$\unicode[STIX]{x1D701}\equiv \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}/r$ is the ratio of azimuthal vorticity to cylindrical radius, and 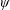 $\unicode[STIX]{x1D713}$ is the Stokes streamfunction in the frame of the ring. Some, but not all, of the
$\unicode[STIX]{x1D713}$ is the Stokes streamfunction in the frame of the ring. Some, but not all, of the 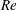 $Re$ dependence in the time evolution of
$Re$ dependence in the time evolution of 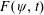 $F(\unicode[STIX]{x1D713},t)$ can be captured by introducing a scaled time
$F(\unicode[STIX]{x1D713},t)$ can be captured by introducing a scaled time 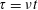 $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D708}t$, where
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D708}t$, where  $\unicode[STIX]{x1D708}$ is the kinematic viscosity. When
$\unicode[STIX]{x1D708}$ is the kinematic viscosity. When 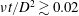 $\unicode[STIX]{x1D708}t/D^{2}\gtrsim 0.02$, the shape of
$\unicode[STIX]{x1D708}t/D^{2}\gtrsim 0.02$, the shape of 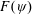 $F(\unicode[STIX]{x1D713})$ is dominated by the linear-in-
$F(\unicode[STIX]{x1D713})$ is dominated by the linear-in-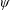 $\unicode[STIX]{x1D713}$ component, the coefficient of the quadratic term being an order of magnitude smaller. An important feature is that, as the dividing streamline (
$\unicode[STIX]{x1D713}$ component, the coefficient of the quadratic term being an order of magnitude smaller. An important feature is that, as the dividing streamline (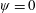 $\unicode[STIX]{x1D713}=0$) is approached,
$\unicode[STIX]{x1D713}=0$) is approached, 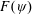 $F(\unicode[STIX]{x1D713})$ tends to a non-zero intercept which exhibits an extra
$F(\unicode[STIX]{x1D713})$ tends to a non-zero intercept which exhibits an extra 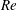 $Re$ dependence. This and other features are explained by a simple toy model consisting of the one-dimensional cylindrical diffusion equation. The key ingredient in the model responsible for the extra
$Re$ dependence. This and other features are explained by a simple toy model consisting of the one-dimensional cylindrical diffusion equation. The key ingredient in the model responsible for the extra 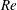 $Re$ dependence is a Robin-type boundary condition, similar to Newton’s law of cooling, that accounts for the edge layer at the dividing streamline.
$Re$ dependence is a Robin-type boundary condition, similar to Newton’s law of cooling, that accounts for the edge layer at the dividing streamline.