Article contents
Almost limiting configurations of steady interfacial overhanging gravity waves
Published online by Cambridge University Press: 09 October 2018
Abstract
We study progressive gravity waves at the interface between two unbounded fluids of different densities. The main concern is to find almost limiting configurations for the so-called overhanging waves. The latter were first computed by Meiron & Saffman (J. Fluid Mech., vol. 129, 1983, pp. 213–218). By means of the Hopf lemma, we rigorously prove that, if 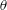 $\unicode[STIX]{x1D703}$ is the angle between the tangent line to the interfacial curve and the horizontal direction, then
$\unicode[STIX]{x1D703}$ is the angle between the tangent line to the interfacial curve and the horizontal direction, then 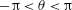 $-\unicode[STIX]{x03C0}<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}$. This inequality allows us to put forward a criterion of proximity of the interface to the limiting configuration, namely, the angle
$-\unicode[STIX]{x03C0}<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}$. This inequality allows us to put forward a criterion of proximity of the interface to the limiting configuration, namely, the angle 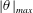 $|\unicode[STIX]{x1D703}|_{max}$ must be close to
$|\unicode[STIX]{x1D703}|_{max}$ must be close to  $\unicode[STIX]{x03C0}$ but may not exceed
$\unicode[STIX]{x03C0}$ but may not exceed  $\unicode[STIX]{x03C0}$. We develop a new numerical method of computing interfacial waves based on the representation of a piecewise-analytic function to be found in such a manner that only the shape of the interface is unknown. All other hydrodynamic quantities can be expressed analytically in terms of functions describing this shape. Using this method, we compute almost limiting configurations of interfacial waves with
$\unicode[STIX]{x03C0}$. We develop a new numerical method of computing interfacial waves based on the representation of a piecewise-analytic function to be found in such a manner that only the shape of the interface is unknown. All other hydrodynamic quantities can be expressed analytically in terms of functions describing this shape. Using this method, we compute almost limiting configurations of interfacial waves with 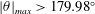 $|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$. Analysing the results of computations, we introduce two new concepts: an inner crest, and an inner solution near the inner crest. These concepts allow us to make a well-grounded prediction for the shapes of limiting interfacial configurations and confirm Saffman & Yuen’s (J. Fluid Mech., vol. 123, 1982, pp. 459–476) conjecture that the waves are geometrically limited.
$|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$. Analysing the results of computations, we introduce two new concepts: an inner crest, and an inner solution near the inner crest. These concepts allow us to make a well-grounded prediction for the shapes of limiting interfacial configurations and confirm Saffman & Yuen’s (J. Fluid Mech., vol. 123, 1982, pp. 459–476) conjecture that the waves are geometrically limited.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 8
- Cited by


