Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T03:42:45.189Z Has data issue: false hasContentIssue false
  • English
  • Français

An entropy-viscosity large eddy simulation study of turbulent flow in a flexible pipe

Published online by Cambridge University Press:  23 November 2018

Zhicheng Wang ,
Michael S. Triantafyllou ,
Yiannis Constantinides  and
George Em Karniadakis
Zhicheng Wang
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA
Michael S. Triantafyllou
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA
Yiannis Constantinides
Affiliation:
Chevron Energy Technology Company, Houston, TX 77002, USA
George Em Karniadakis*
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: George_Karniadakis@Brown.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a new approach – the entropy-viscosity method (EVM) – for numerical modelling of high Reynolds number flows and investigate its potential by simulating fully developed incompressible turbulent flow, first in a stationary pipe and subsequently in a flexible pipe. This method, which was first proposed by Guermond et al. (J. Comput. Phys., vol. 230 (11), 2011, pp. 4248–4267), introduces the concept of entropy viscosity, computed based on the nonlinear localized residual obtained from the energy equation. Specifically, this nonlinear viscosity based on the local size of entropy production is added to the spectral element discretization employed in our work for stabilization at insufficient resolution. Unlike its original formulation, which includes an ad hoc tuneable parameter $\unicode[STIX]{x1D6FC}$, here, we determine the value of $\unicode[STIX]{x1D6FC}$ by assuming that the entropy viscosity is analogous to the eddy viscosity of the Smagorinsky model. However, the overall approach has the flavour of the implicit large eddy simulation (ILES) instead of the standard large eddy simulation (LES). Given the empiricism of our approach, we have performed systematic studies of homogeneous isotropic turbulence for validation (see appendix A). We have also carried out a more complete numerical simulation study to investigate incompressible turbulent flow in a stationary pipe at 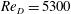$Re_{D}=5300$ and 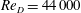$Re_{D}=44\,000$, following the work of Wu & Moin (J. Fluid Mech., vol. 608, 2008, pp. 81–112) who performed very accurate direct numerical simulations (DNS) of these two cases. We found that the mean flow, turbulence fluctuations, and two-point correlations of the EVM-based LES are in good agreement with the DNS of Wu & Moin despite the fact that we employed grids with resolution two orders of magnitude smaller. If we instead use the standard Smagorinsky model in our simulations, the computations become unstable due to insufficient resolution of the smaller scales. Another important difference is that the entropy-viscosity model scales with the cube of the distance from the wall and approaches zero at the wall, which is theoretically correct, as shown by our a posteriori tests. Based on the validated EVM approach, we then simulated fully developed turbulent flow at 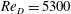$Re_{D}=5300$ in a flexible pipe subject to prescribed vibrations in the cross-flow plane corresponding to a standing wave of amplitude 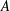$A$ and wavelength 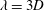$\unicode[STIX]{x1D706}=3D$, where 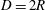$D=2R$ is the pipe diameter and 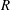$R$ is the radius. We have simulated 11 cases corresponding to increasing values of wave steepness 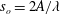$s_{o}=2A/\unicode[STIX]{x1D706}$, with 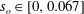$s_{o}\in [0,0.067]$. We found a quadratic dependence of the friction factor on 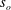$s_{o}$ with the minimum at approximately 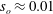$s_{o}\approx 0.01$, so, surprisingly, we have a slight decrease in drag at first and then a substantial increase compared to the stationary pipe. To obtain the turbulence statistics, we averaged the simulated flow over twenty time periods at the nodes and anti-nodes separately. We found substantial changes in the mean velocity profile at distances 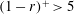$(1-r)^{+}>5$ while the peaks of turbulent intensities were amplified by 50 % in the axial direction and by 200 % in the normal and azimuthal directions at 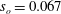$s_{o}=0.067$. The peak shear stress at the node increased by more than 200 % whereas at the anti-node it attained negative values. Turbulent budgets revealed large changes close to the wall at 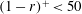$(1-r)^{+}<50$ while flow visualizations showed that many more strong worm-like vortices were generated in the near-wall regions compared to the stationary pipe. We have also computed various spatio-temporal correlations that show that the pressure fluctuations are very sensitive to the pipe vibration and scale quadratically with $s_{o}$. Both pressure and velocity correlations exhibit cellular patterns consistent with the standing-wave pipe motion.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 691 - 730
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arndt, D., Bangerth, W., Davydov, D., Heister, T., Heltai, L., Kronbichler, M., Maier, M., Pelteret, J.-P., Turcksin, B. & Wells, D. 2017 The deal.II library, version 8.5. J. Numer. Math. 25, 137–146.Google Scholar
Bardina, J., Ferziger, J. & Reynolds, W. 1980 Improved subgrid-scale models for large-eddy simulation. In 13th Fluid and Plasma Dynamics Conference, Fluid Dynamics and Co-located Conferences, vol. 80. AIAA.Google Scholar
Boris, J. P., Grinstein, F. F., Oran, E. S. & Kolbe, R. L. 1992 New insights into large eddy simulation. Fluid Dyn. Res. 10 (4–6), 199–228.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1971 Simple Eulerian time correlation of full and narrow-band velocity signals in grid-generated ‘isotropic’ turbulence. J. Fluid Mech. 48, 273–337.Google Scholar
Fureby, C. & Grinstein, F. F. 1999 Monotonically integrated large eddy simulation of free shear flows. AIAA J. 37 (5), 544–556.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid scale eddy viscosity model. Phys. Fluids 3 (7), 1760–1765.Google Scholar
Geurts, B. 2004 Elements of Direct and Large-Eddy Simulation. R.T. Edwards.Google Scholar
Grinstein, F., Margonin, L. & Rider, W. 2007 Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics. Cambridge University Press.Google Scholar
Guermond, J. L. 2008 On the use of the notion of suitable weak solutions in CFD. Intl J. Numer. Meth. Fluids 57 (9), 1153–1170.Google Scholar
Guermond, J. L., Larios, A. & Thompson, T. 2015 Validation of an entropy-viscosity model for large eddy simulation. In Direct and Large-Eddy Simulation IX, ERCOFTAC Series, vol. 20, pp. 43–48. Springer.Google Scholar
Guermond, J. L., Nazarov, M. & Popov, B.2011a Implementation of the entropy viscosity method. Tech. Rep., KTH, Numerical Analysis Group.Google Scholar
Guermond, J. L., Pasquetti, R. & Popov, B. 2011b Entropy viscosity method for nonlinear conservation law. J. Comput. Phys. 230 (11), 4248–4267.Google Scholar
Guermond, J. L., Pasquetti, R. & Popov, B. 2011c From suitable weak solutions to entropy viscosity. J. Sci. Comput. 49 (1), 35–50.Google Scholar
Hughes, T. J. R., Feijóo, G. R., Mazzei, L. & Quincy, J. B. 1998 The variational multiscale method – a paradigm for mechanics. Comput. Meth. Appl. Mech. Engng 166 (1–2), 3–24.Google Scholar
Hughes, T. J. R., Oberai, A. A. & Mazzei, L. 2001 Large eddy simulation of turbulent channel flows by the variational multiscale method. Phys. Fluids 133 (6), 1784–1799.Google Scholar
Karamanos, G. S. & Karniadakis, G. E. 2000 A spectral vanishing viscosity method for large-eddy simulations. J. Comput. Phys. 163 (1), 22–50.Google Scholar
Karniadakis, G. E. & Sherwin, S. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Keirsbulck, L., Labraga, L. & el Hak, M. G. 2012 Statistical properties of wall shear stress fluctuations in turbulent channel flows. Intl J. Heat Fluid Flow 37, 1–8.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kim, J. & Sung, H. J. 2006 Wall pressure fluctuations and flow-induced noise in a turbulent boundary layer over a bump. J. Fluid Mech. 558, 79–102.Google Scholar
Lesieur, M. & Metais, O. 1996 New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 28, 45–82.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid scale closure method. Phys. Fluids 3, 633–635.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Nazarov, M., Guermond, J. L. & Popov, B.2011 A posteriori error estimation for the compressible Euler equations using entropy viscosity. Tech. Rep. KTH, Numerical Analysis Group.Google Scholar
Nazarov, M. & Larcher, A. 2017 Numerical investigation of a viscous regularization of the Euler equations by entropy viscosity. Comput. Meth. Appl. Mech. Engng 317, 128–152.Google Scholar
Newman, D. J. & Karniadakis, G. E. 1997 A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 344, 95–136.Google Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62, 183–200.Google Scholar
Orlandi, P. 2000 Fluid Flow Phenomena: A Numerical Toolkit. Kluwer Academic.Google Scholar
Paidoussis, M. P. 1998 Fluid-Structure Interactions: Slender Structures and Axial Flow, vol. 1. Academic Press.Google Scholar
Paidoussis, M. P. 2004 Fluid-Structure Interactions: Slender Structures and Axial Flow, vol. 2. Academic Press.Google Scholar
Piomelli, U. 2008 Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci. 44, 437–446.Google Scholar
Pittard, M. T., Evans, R. P., Maynes, R. D. & Blottera, J. D. 2004 Experimental and numerical investigation of turbulent flow induced pipe vibration in fully developed flow. Rev. Sci. Instrum. 75 (7), 2393–2401.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pope, S. B. 2004 Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 6, 35–59.Google Scholar
Sagaut, P. 2006 Large Eddy Simulation for Incompressible Flow. An Introduction, 3rd edn. Springer.Google Scholar
Sarghini, F., Piomelli, U. & Balaras, E. 1999 Scale-similar models for large-eddy simulations. Phys. Fluids 11 (6), 1596–1607.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.Google Scholar
Tadmor, E. 1989 Convergence of spectral methods for nonlinear conservation laws. SIAM J. Numer. Anal. 26, 30–44.Google Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.Google Scholar
Xie, F., Zheng, X., Triantafyllou, M. S., Constantinides, Y. & Karniadakis, G. E. 2016 The flow dynamics of the garden-hose instability. J. Fluid Mech. 800, 595–612.Google Scholar
Xu, C. J. & Pasquetti, R. 2004 Stabilized spectral element computations of high Reynolds number incompressible flows. J. Comput. Phys. 196 (2), 680–704.Google Scholar