Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Johnson, B. M.
2014.
Closed-form shock solutions.
Journal of Fluid Mechanics,
Vol. 745,
Issue. ,
Fernandez-Feria, R.
2016.
Heavy gas relaxation in a light gas shock wave at small Prandtl number.
Physical Review E,
Vol. 94,
Issue. 3,
Christov, Ivan C.
2016.
Nonlinear acoustics and shock formation in lossless barotropic Green--Naghdi fluids.
Evolution Equations and Control Theory,
Vol. 5,
Issue. 3,
p.
349.
Johnson, B. M.
and
Klein, R. I.
2017.
Three-temperature plasma shock solutions with gray radiation diffusion.
Shock Waves,
Vol. 27,
Issue. 2,
p.
281.
Jackson, Haran
2017.
A fast numerical scheme for the Godunov–Peshkov–Romenski model of continuum mechanics.
Journal of Computational Physics,
Vol. 348,
Issue. ,
p.
514.
Eyink, Gregory L.
and
Drivas, Theodore D.
2018.
Cascades and Dissipative Anomalies in Compressible Fluid Turbulence.
Physical Review X,
Vol. 8,
Issue. 1,
Zhao, Dongxiao
and
Aluie, Hussein
2018.
Inviscid criterion for decomposing scales.
Physical Review Fluids,
Vol. 3,
Issue. 5,
Patel, A.
and
Singh, M.
2019.
Exact solution of shock wave structure in a non-ideal gas under constant and variable coefficient of viscosity and heat conductivity.
Shock Waves,
Vol. 29,
Issue. 3,
p.
427.
Uribe, F. J.
and
Velasco, R. M.
2019.
Exact solutions for shock waves in dilute gases.
Physical Review E,
Vol. 100,
Issue. 2,
Raman, Senthilkumar
and
Kim, Heuy Dong
2019.
31st International Symposium on Shock Waves 2.
p.
751.
Domínguez-Vázquez, D.
and
Fernandez-Feria, R.
2019.
On analytical approximations for the structure of a shock wave in a fully ionized plasma.
Physics of Plasmas,
Vol. 26,
Issue. 8,
Khapra, D.
and
Patel, A.
2020.
Shock wave structure in non-ideal dilute gases under variable Prandtl number.
Shock Waves,
Vol. 30,
Issue. 6,
p.
585.
Zhang, Fan
Cheng, Jian
and
Liu, Tiegang
2020.
An asymptotic expansion for 1D steady compressible Navier‐Stokes equations under nonuniform enthalpy.
Mathematical Methods in the Applied Sciences,
Vol. 43,
Issue. 9,
p.
5788.
Zhang, Fan
Cheng, Jian
and
Liu, Tiegang
2020.
Exponential boundary-layer approximation space for solving the compressible laminar Navier-Stokes equations.
Advances in Computational Mathematics,
Vol. 46,
Issue. 2,
Guermond, Jean-Luc
Maier, Matthias
Popov, Bojan
and
Tomas, Ignacio
2021.
Second-order invariant domain preserving approximation of the compressible Navier–Stokes equations.
Computer Methods in Applied Mechanics and Engineering,
Vol. 375,
Issue. ,
p.
113608.
Guermond, Jean-Luc
Kronbichler, Martin
Maier, Matthias
Popov, Bojan
and
Tomas, Ignacio
2022.
On the implementation of a robust and efficient finite element-based parallel solver for the compressible Navier–Stokes equations.
Computer Methods in Applied Mechanics and Engineering,
Vol. 389,
Issue. ,
p.
114250.
Timokhin, M.Yu.
Kudryavtsev, A.N.
and
Bondar, Ye.A.
2022.
The Mott-Smith solution to the regular shock reflection problem.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Khapra, Divya
and
Patel, Arvind
2022.
Shock-wave structure in non-polar diatomic and polyatomic dense gases under rotation and vibration.
Physics of Fluids,
Vol. 34,
Issue. 6,
Uribe, Francisco J.
and
Velasco, Rosa M.
2023.
Nonlinear transport coefficients from Grad’s 13–moment approximation.
Meccanica,
Vol. 58,
Issue. 6,
p.
1099.
Cao, Kui
and
Liu, Tiegang
2023.
Asymptotic expansion for 1D steady nonuniform enthalpy compressible supersonic flow at high Reynolds number.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 2,
p.
2249.
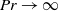 $\mathit{Pr}\rightarrow \infty $ and
$\mathit{Pr}\rightarrow \infty $ and 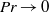 $\mathit{Pr}\rightarrow 0$ limits (where
$\mathit{Pr}\rightarrow 0$ limits (where 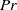 $\mathit{Pr}$ is the Prandtl number). The solutions are analogous to the
$\mathit{Pr}$ is the Prandtl number). The solutions are analogous to the 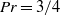 $\mathit{Pr}= 3/ 4$ solution discovered by Becker and analytically capture the profile of shock fronts in ideal gases. The large-
$\mathit{Pr}= 3/ 4$ solution discovered by Becker and analytically capture the profile of shock fronts in ideal gases. The large-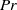 $\mathit{Pr}$ solution is very similar to Becker’s solution, differing only by a scale factor. The small-
$\mathit{Pr}$ solution is very similar to Becker’s solution, differing only by a scale factor. The small-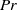 $\mathit{Pr}$ solution is qualitatively different, with an embedded isothermal shock occurring above a critical Mach number. Solutions are derived for constant viscosity and conductivity as well as for the case in which conduction is provided by a radiation field. For a completely general density- and temperature-dependent viscosity and conductivity, the system of equations in all three limits can be reduced to quadrature. The maximum error in the analytical solutions when compared to a numerical integration of the finite-
$\mathit{Pr}$ solution is qualitatively different, with an embedded isothermal shock occurring above a critical Mach number. Solutions are derived for constant viscosity and conductivity as well as for the case in which conduction is provided by a radiation field. For a completely general density- and temperature-dependent viscosity and conductivity, the system of equations in all three limits can be reduced to quadrature. The maximum error in the analytical solutions when compared to a numerical integration of the finite-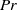 $\mathit{Pr}$ equations is
$\mathit{Pr}$ equations is 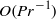 $\mathit{O}({\mathit{Pr}}^{- 1} )$ as
$\mathit{O}({\mathit{Pr}}^{- 1} )$ as 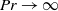 $\mathit{Pr}\rightarrow \infty $ and
$\mathit{Pr}\rightarrow \infty $ and 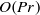 $\mathit{O}(\mathit{Pr})$ as
$\mathit{O}(\mathit{Pr})$ as 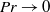 $\mathit{Pr}\rightarrow 0$.
$\mathit{Pr}\rightarrow 0$.

