Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T23:32:30.222Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of heat transfer in two-dimensional turbulent convection with high-porosity fluid-saturated media

Published online by Cambridge University Press:  30 July 2021

Wei Qiang Open the ORCID record for Wei Qiang [Opens in a new window] ,
Mingli Xie ,
Zhikang Liu ,
Yong Wang ,
Hui Cao  and
Hanwen Zhou
Wei Qiang*
Affiliation:
School of Computer Science, China University of Geosciences, Wuhan 430078, PR China
Mingli Xie
Affiliation:
School of Computer Science, China University of Geosciences, Wuhan 430078, PR China
Zhikang Liu
Affiliation:
School of Computer Science, China University of Geosciences, Wuhan 430078, PR China
Yong Wang
Affiliation:
School of Computer Science, China University of Geosciences, Wuhan 430078, PR China
Hui Cao
Affiliation:
School of Automation, China University of Geosciences, Wuhan 430074, PR China
Hanwen Zhou
Affiliation:
School of Earth Science, China University of Geosciences, Wuhan 430074, PR China
*
†Email address for correspondence: qw@cug.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

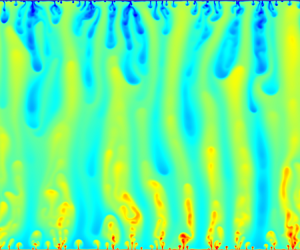
We study the asymptotic behaviour of convective heat transfer for turbulent flows in high-porosity fluid-saturated media by two-dimensional high-resolution numerical simulation. The generalized Navier–Stokes equations for incompressible fluid flow and the heat transport equation in porous media at the representative element volume scale are solved by the lattice Boltzmann method, wherein the non-Darcian effects are taken into consideration. The asymptotic behaviour of the Nusselt number $N$ has been revealed for Rayleigh numbers $10^4\leq R\leq 10^{11}$ and Darcy numbers $10^{-6}\leq \xi \leq 10^6$: all the data for various Darcy numbers gradually collapse onto a unique line with increasing Rayleigh number. The asymptote can be well represented by $N=0.146\times R^{0.286}$ for $R>2\times 10^7$, which approaches the relationship for the Rayleigh–Bénard turbulent convection of free fluid flows. The transition can be characterized by a scaling analysis with $R^{}\xi ^{3/2}\sim 1$, below which, however, the data collapse onto the Darcy limit for porous media. The Reynolds number and the Nusselt number both increase with Darcy number above the onset of convection, whereas a premature saturation of the Nusselt number is observed in comparison with that of the Reynolds number. The counter-gradient heat transport by the large-scale flows is quantified, which compensates for the increase of the gradient heat transport with Darcy number. The heat transfer in high-porosity fluid-saturated media with a very small Darcy number $\xi \geq 10^{-6}$ can be comparable to that of free fluid flows for a sufficiently high Rayleigh number $R\geq 10^{11}$.

JFM classification

Convection: Convection in porous media Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A30
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.10.1103/RevModPhys.81.503CrossRefGoogle Scholar
Backhaus, S., Turitsyn, K. & Ecke, R.E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106 (10), 104501.10.1103/PhysRevLett.106.104501CrossRefGoogle Scholar
Bejan, A. 1987 The basic scales of natural convection heat and mass transfer in fluids and fluid-saturated porous media. Intl Commun. Heat Mass Transfer 14 (2), 107–123.10.1016/S0735-1933(87)81002-3CrossRefGoogle Scholar
Bhatnagar, P.L., Gross, E.P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component system. Phys. Rev. 94, 511–525.10.1103/PhysRev.94.511CrossRefGoogle Scholar
Braga, E.J. & de Lemos, M.J.S. 2009 Laminar and turbulent free convection in a composite enclosure. Intl J. Heat Mass Transfer 52 (3), 588–596.10.1016/j.ijheatmasstransfer.2008.07.012CrossRefGoogle Scholar
Calmidi, V.V. 1998 Transport phenomena in high porosity metal foams. PhD thesis, University of Colorado.Google Scholar
Castaing, B., Gunaratne, G., Kadanoff, L., Libchaber, A. & Heslot, F. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.10.1017/S0022112089001643CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.10.1140/epje/i2012-12058-1CrossRefGoogle ScholarPubMed
Ching, E.S.C., Guo, H., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Extraction of plumes in turbulent thermal convection. Phys. Rev. Lett. 93, 124501.CrossRefGoogle ScholarPubMed
Darcy, H. 1856 Les fontaines publiques de la ville de Dijon: exposition et application. Victor Dalmont.Google Scholar
Davidson, J.H., Kulacki, F.A. & Savela, D. 2009 Natural convection in water-saturated reticulated vitreous carbon foam. Intl J. Heat Mass Transfer 52 (19), 4479–4483.10.1016/j.ijheatmasstransfer.2009.03.051CrossRefGoogle Scholar
Doering, C.R. & Constantin, P. 1998 Bounds for heat transport in a porous layer. J. Fluid Mech. 376, 263–296.10.1017/S002211209800281XCrossRefGoogle Scholar
Elder, J.W. 1967 Steady free convection in a porous medium heated from below. J. Fluid Mech. 27, 29–48.10.1017/S0022112067000023CrossRefGoogle Scholar
Ergun, S. 1952 Fluid flow through packed columns. Chem. Engng Prog. 48, 89–94.Google Scholar
Fu, X., Cueto-Felgueroso, L. & Juanes, R. 2013 Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. A 371 (2004), 20120355.CrossRefGoogle ScholarPubMed
Gasteuil, Y., Shew, W.L., Gibert, M., Chillá, F., Castaing, B. & Pinton, J.-F. 2007 Lagrangian temperature, velocity, and local heat flux measurement in Rayleigh–Bénard convection. Phys. Rev. Lett. 99, 234302.CrossRefGoogle ScholarPubMed
Georgiadis, J.G. & Catton, I. 1986 Prandtl number effect on Benard convection in porous media. J. Heat Transfer 108 (2), 284–290.CrossRefGoogle Scholar
Graham, M.D. & Steen, P.H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–90.CrossRefGoogle Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh-Bénard convection. J. Comput. Phys. 49 (2), 241–264.10.1016/0021-9991(83)90125-0CrossRefGoogle Scholar
Guo, Z. & Zhao, T.S. 2002 Lattice Boltzmann model for incompressible flows through porous media. Phys. Rev. E 66 (3), 036304.10.1103/PhysRevE.66.036304CrossRefGoogle ScholarPubMed
Guo, Z. & Zhao, T.S. 2005 A lattice Boltzmann model for convection heat transfer in porous media. Numer. Heat Transfer B 47 (2), 157–177.10.1080/10407790590883405CrossRefGoogle Scholar
Guo, Z., Zheng, C. & Shi, B. 2002 An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 14 (6), 2007–2010.CrossRefGoogle Scholar
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.10.1103/PhysRevLett.108.224503CrossRefGoogle Scholar
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2014 High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.10.1017/jfm.2014.216CrossRefGoogle Scholar
Hidalgo, J.J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.10.1103/PhysRevLett.109.264503CrossRefGoogle ScholarPubMed
Hirasawa, S., Tsubota, R., Kawanami, T. & Shirai, K. 2013 Reduction of heat loss from solar thermal collector by diminishing natural convection with high-porosity porous medium. Trans. ASME: J. Sol. Energy 97, 305–313.Google Scholar
Hong, J.T., Tien, C.L. & Kaviany, M. 1985 Non-Darcian effects on vertical-plate natural convection in porous media with high porosities. Intl J. Heat Mass Transfer 28 (11), 2149–2157.CrossRefGoogle Scholar
Hsu, C.T. & Cheng, P. 1990 Thermal dispersion in a porous medium. Intl J. Heat Mass Transfer 33 (8), 1587–1597.10.1016/0017-9310(90)90015-MCrossRefGoogle Scholar
Huang, Y.-X. & Zhou, Q. 2013 Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 737, R3.CrossRefGoogle Scholar
Johnston, H. & Doering, C.R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.CrossRefGoogle ScholarPubMed
Joseph, D.D., Nield, D.A. & Papanicolaou, G. 1982 Nonlinear equation governing flow in a saturated porous medium. Water Resour. Res. 18 (4), 1049–1052.10.1029/WR018i004p01049CrossRefGoogle Scholar
Kimura, S., Schubert, G. & Straus, J.M. 1986 Route to chaos in porous-medium thermal convection. J. Fluid Mech. 166, 305–324.10.1017/S0022112086000162CrossRefGoogle Scholar
Kladias, N. & Prasad, V. 1989 Natural convection in horizontal porous layers: effects of Darcy and Prandtl numbers. Trans. ASME J. Heat Transfer 111 (4), 926–935.CrossRefGoogle Scholar
Kladias, N. & Prasad, V. 1991 Experimental verification of Darcy-Brinkman-Forchheimer flow model for natural convection in porous media. J. Thermophys. Heat Transfer 5 (4), 560–576.CrossRefGoogle Scholar
Kopanidis, A., Theodorakakos, A., Gavaises, E. & Bouris, D. 2010 3D numerical simulation of flow and conjugate heat transfer through a pore scale model of high porosity open cell metal foam. Intl J. Heat Mass Transfer 53 (11), 2539–2550.CrossRefGoogle Scholar
Kuntz, D. & Grathwohl, P. 2009 Comparison of steady-state and transient flow conditions on reactive transport of contaminants in the vadose soil zone. J. Hydrology 369 (3–4), 225–233.CrossRefGoogle Scholar
Lage, J.L. 1992 Effect of the convective inertia term on Bénard convection in a porous medium. Numer. Heat Transfer 22 (4), 469–485.CrossRefGoogle Scholar
Lage, J.L., Bejan, A. & Georgiadis, J.G. 1992 The Prandtl number effect near the onset of Bénard convection in a porous medium. Intl J. Heat Fluid Flow 13 (4), 408–411.CrossRefGoogle Scholar
Letelier, J.A., Mujica, N. & Ortega, J.H. 2019 Perturbative corrections for the scaling of heat transport in a Hele-Shaw geometry and its application to geological vertical fractures. J. Fluid Mech. 864, 746–767.CrossRefGoogle Scholar
Lister, C.R.B. 1990 An explanation for the multivalued heat transport found experimentally for convection in a porous medium. J. Fluid Mech. 214, 287–320.CrossRefGoogle Scholar
Liu, S. & Masliyah, J.H. 2005 Dispersion in porous media. In Handbook of Porous Media (ed. K. Vafai), pp. 81–140. Taylor & Francis.CrossRefGoogle Scholar
Lohse, D. & Toschi, F. 2003 Ultimate state of thermal convection. Phys. Rev. Lett. 90, 034502.10.1103/PhysRevLett.90.034502CrossRefGoogle ScholarPubMed
Neufeld, J.A., Hesse, M.A., Riaz, A., Hallworth, M.A., Tchelepi, H.A. & Huppert, H.E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37 (22), L22404.CrossRefGoogle Scholar
Nield, D.A. 1991 The limitations of the Brinkman-Forchheimer equation in modeling flow in a saturated porous medium and at an interface. Intl J. Heat Fluid Flow 12 (3), 269–272.CrossRefGoogle Scholar
Nield, D.A. 1994 Modelling high speed flow of a compressible fluid in a saturated porous medium. Transp. Porous Med. 14 (1), 85–88.CrossRefGoogle Scholar
Nield, D.A & Bejan, A. 2013 Convection in Porous Media. Springer.CrossRefGoogle Scholar
Nield, D.A. & Joseph, D.D. 1985 Effects of quadratic drag on convection in a saturated porous medium. Phys. Fluids 28 (3), 995–997.CrossRefGoogle Scholar
Nield, D.A. & Kuznetsov, A.V. 2013 An historical and topical note on convection in porous media. J. Heat Transfer 135 (6), 061201.CrossRefGoogle Scholar
Nithiarasu, P., Seetharamu, K.N. & Sundararajan, T. 1997 Natural convective heat transfer in a fluid saturated variable porosity medium. Intl J. Heat Mass Transfer 40 (16), 3955–3967.CrossRefGoogle Scholar
Orr, F.M. 2009 Onshore geologic storage of CO$_2$. Science 325 (5948), 1656–1658.CrossRefGoogle Scholar
Otero, J., Dontcheva, L.A., Johnston, H., Worthing, R.A., Kurganov, A., Petrova, G. & Doering, C.R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.CrossRefGoogle Scholar
van der Poel, E.P., Stevens, R.J.A.M. & Lohse, D. 2013 Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.CrossRefGoogle Scholar
Qian, Y.H., D'Humières, D. & Lallemand, P. 1992 Lattice BGK models for Navier–Stokes equation. Europhys. Lett. 17 (6), 479–484.CrossRefGoogle Scholar
Qiang, W. & Cao, H. 2014 Flow patterns in inclined-layer turbulent convection. Eur. Phys. J. E 37 (7), 64.CrossRefGoogle ScholarPubMed
Qiang, W., Cao, H., Li, W. & Zhang, F. 2017 Counter-gradient heat transport by large-scale circulation in two-dimensional turbulent convection. Europhys. Lett. 118 (6), 64001.CrossRefGoogle Scholar
Randolph, J.B. & Saar, M.O. 2011 Combining geothermal energy capture with geologic carbon dioxide sequestration. Geophys. Res. Lett. 38 (10), L10401.CrossRefGoogle Scholar
Rudraiah, N., Veerappa, B. & Rao, S.B. 1982 Convection in a fluid-saturated porous layer with non-uniform temperature gradient. Intl J. Heat Mass Transfer 25 (8), 1147–1156.CrossRefGoogle Scholar
Schmalzl, J., Breuer, M. & Hansen, U. 2000 On the validity of two-dimensional numerical approaches to time-dependent thermal convection. Europhys. Lett. 67 (3), 390–396.CrossRefGoogle Scholar
Schumacher, J. 2009 Lagrangian studies in convective turbulence. Phys. Rev. E 79, 056301.CrossRefGoogle ScholarPubMed
Shan, X. 1997 Simulation of Rayleigh–Bénard convection using a lattice Boltzmann method. Phys. Rev. E 55, 2780–2788.10.1103/PhysRevE.55.2780CrossRefGoogle Scholar
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2003 Measured local heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 90, 074501.CrossRefGoogle ScholarPubMed
Shishkina, O., Stevens, R.J.A.M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.CrossRefGoogle Scholar
Slim, A. 2014 Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech. 741, 461–491.CrossRefGoogle Scholar
Sun, M., Hu, C., Zha, L., Xie, Z., Yang, L., Tang, D., Song, Y. & Zhao, J. 2020 Pore-scale simulation of forced convection heat transfer under turbulent conditions in open-cell metal foam. Chem. Engng J. 389, 124427.CrossRefGoogle Scholar
Vadasz, P. 1999 Local and global transitions to chaos and hysteresis in a porous layer heated from below. Transp. Porous Media 37 (2), 213–245.CrossRefGoogle Scholar
Vafai, K. & Tien, C.L. 1981 Boundary and inertia effects on flow and heat transfer in porous media. Intl J. Heat Mass Transfer 24 (2), 195–203.CrossRefGoogle Scholar
Vishnampet, R., Narasimhan, A. & Babu, V. 2011 High Rayleigh number natural convection inside 2D porous enclosures using the lattice Boltzmann method. J. Heat Transfer 133 (6), 062501.CrossRefGoogle Scholar
Wang, M. & Bejan, A. 1987 Heat transfer correlation for Bénard convection in a fluid saturated porous layer. Intl Commun. Heat Mass Transfer 14 (6), 617–626.CrossRefGoogle Scholar
Whitaker, S. 1969 Advances in theory of fluid motion in porous media. Ind. Engng Chem. 61 (12), 14–28.10.1021/ie50720a004CrossRefGoogle Scholar
Whitaker, S. 1999 The Method of Volume Averaging. Kluwer.CrossRefGoogle Scholar
Wooding, R.A. 1957 Steady state free thermal convection of liquid in a saturated permeable medium. J. Fluid Mech. 2 (3), 273–285.CrossRefGoogle Scholar
Zhao, C.Y. 2012 Review on thermal transport in high porosity cellular metal foams with open cells. Intl J. Heat Mass Transfer 55 (13), 3618–3632.CrossRefGoogle Scholar