Article contents
Barotropic theory for the velocity profile of Jupiter’s turbulent jets: an example for an exact turbulent closure
Published online by Cambridge University Press: 07 December 2018
Abstract
We model the dynamics of Jupiter’s jets by the stochastic barotropic 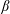 $\unicode[STIX]{x1D6FD}$-plane model. In this simple framework, by analytic computation of the averaged effect of eddies, we obtain three new explicit results about the equilibrium structure of jets. First we obtain a very simple explicit relation between the Reynolds stresses, the energy injection rate and the averaged velocity shear. This predicts the averaged velocity profile far from the jet edges (extrema of zonal velocity). Our approach takes advantage of a time-scale separation between the inertial dynamics on one hand, and the spin-up (or spin-down) time on the other. Second, a specific asymptotic expansion close to the eastward jet extremum explains the formation of a cusp at the scale of energy injection, characterized by a curvature that is independent of the forcing spectrum. Finally, we derive equations that describe the evolution of the westward tip of the jets. The analysis of these equations is consistent with the previously discussed picture of barotropic adjustment, explaining the relation between the westward jet curvature and the
$\unicode[STIX]{x1D6FD}$-plane model. In this simple framework, by analytic computation of the averaged effect of eddies, we obtain three new explicit results about the equilibrium structure of jets. First we obtain a very simple explicit relation between the Reynolds stresses, the energy injection rate and the averaged velocity shear. This predicts the averaged velocity profile far from the jet edges (extrema of zonal velocity). Our approach takes advantage of a time-scale separation between the inertial dynamics on one hand, and the spin-up (or spin-down) time on the other. Second, a specific asymptotic expansion close to the eastward jet extremum explains the formation of a cusp at the scale of energy injection, characterized by a curvature that is independent of the forcing spectrum. Finally, we derive equations that describe the evolution of the westward tip of the jets. The analysis of these equations is consistent with the previously discussed picture of barotropic adjustment, explaining the relation between the westward jet curvature and the 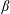 $\unicode[STIX]{x1D6FD}$-effect. Our results give a consistent overall theory of the stationary velocity profile of inertial barotropic zonal jets, in the limit of small-scale forcing.
$\unicode[STIX]{x1D6FD}$-effect. Our results give a consistent overall theory of the stationary velocity profile of inertial barotropic zonal jets, in the limit of small-scale forcing.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 8
- Cited by

