Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T03:23:41.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Barotropic to baroclinic energy conversion using a time-varying background density

Published online by Cambridge University Press:  11 May 2021

Sorush Omidvar Open the ORCID record for Sorush Omidvar [Opens in a new window] ,
Mohammadreza Davoodi Open the ORCID record for Mohammadreza Davoodi [Opens in a new window]  and
C. Brock Woodson Open the ORCID record for C. Brock Woodson [Opens in a new window]
Sorush Omidvar*
Affiliation:
School of Environmental, Civil, Agricultural, and Mechanical Engineering, University of Georgia, Athens, GA30602, USA
Mohammadreza Davoodi
Affiliation:
UT Arlington Research Institute, University of Texas at Arlington, Fort Worth, TX76118, USA
C. Brock Woodson
Affiliation:
School of Environmental, Civil, Agricultural, and Mechanical Engineering, University of Georgia, Athens, GA30602, USA
*
†Email address for correspondence: sorush.omidvar@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

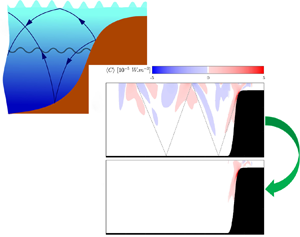
Internal wave generation is fundamentally the conversion of barotropic to baroclinic energy that often occurs due to vertical acceleration of stratified flows over topographic features. Acceleration results in a phase lag between density (pressure) perturbations and the barotropic velocity. To estimate the conversion of barotropic to baroclinic energy, the density perturbation is often calculated using a time-invariant background density. Other phenomena, however, can also alter the phasing of density perturbations and vertical velocities, such as barotropic tidal heaving and internal wave interactions. Consequently, accurately accounting for these dynamics in energy budgets is important. Tidal averaging or modal decomposition are often used to isolate topographic energy conversion in the presence of these other phenomena. However, while effective, these methods do not provide insights into the dynamics of conversion either through time or over depth. Here, we present a new analytical approach to calculating barotropic to baroclinic conversion using a time-varying background density. Our method results in an additional term in the baroclinic energy budget that directly accounts for barotropic tidal heaving and internal wave interactions, depending on the formulation of the background density. The tidally averaged, domain-integrated conversion rate is consistent across methods. Isolation of topographic conversion demonstrates that conversion due to interactions between internal wave beams and barotropic tidal heaving lead to relatively small differences in the overall conversion. However, using a time-varying background density allows for full decomposition of barotropic to baroclinic conversion through time and the identification of regions where negative conversion related to mixing actually occurs.

JFM classification

Geophysical and Geological Flows: Coastal engineering Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Ocean processes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 918 , 10 July 2021 , A26
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baines, P.G. 1974 The generation of internal tides over steep continental slopes. Phil. Trans. R. Soc. Lond. A 277 (1263), 27–58.Google Scholar
Baines, P.G. 1982 On internal tide generation models. Deep-Sea Res. A 29 (3), 307–338.CrossRefGoogle Scholar
Bell, T.H. 1975 Topographically generated internal waves in the open ocean. J. Geophys. Res. 80 (3), 320–327.CrossRefGoogle Scholar
Carter, G.S., Merrifield, M.A., Becker, J.M., Katsumata, K., Gregg, M.C., Luther, D.S., Levine, M.D., Boyd, T.J. & Firing, Y.L. 2008 Energetics of M 2 barotropic-to-baroclinic tidal conversion at the Hawaiian Islands. J. Phys. Oceanogr. 38 (10), 2205–2223.CrossRefGoogle Scholar
Cushman-Roisin, B. & Beckers, J.-M. 2013 Introduction to geophysical fluid dynamics.Google Scholar
Dossmann, Y., Pollet, F., Odier, P. & Dauxois, T. 2017 Mixing and formation of layers by internal wave forcing. J. Geophys. Res. 122 (12), 9906–9917.CrossRefGoogle Scholar
Egbert, G.D. & Ray, R.D. 2000 Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405 (6788), 775–778.CrossRefGoogle ScholarPubMed
Fringer, O.B., Gerritsen, M. & Street, R.L. 2006 An unstructured-grid, finite-volume, nonhydrostatic, parallel coastal ocean simulator. Ocean Model. 14 (3), 139–173.CrossRefGoogle Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39, 57–87.CrossRefGoogle Scholar
Garrett, C. & Munk, W. 1979 Internal waves in the ocean. Annu. Rev. Fluid Mech. 11 (1), 339–369.CrossRefGoogle Scholar
Gerkema, T., Lam, F.P.A. & Maas, L.R.M. 2004 Internal tides in the Bay of Biscay: conversion rates and seasonal effects. Deep-Sea Res. II 51 (25–26 Special Issue), 2995–3008.CrossRefGoogle Scholar
Gill, A.E. 1982 Waves of large horizontal scale: Normal modes. In Atmosphere–Ocean Dynamics (ed. W. L. Donn), pp. 159–162. Academic Press.Google Scholar
Holloway, P.E. & Merrifield, M.A. 1999 Internal tide generation by seamounts, ridges, and islands. J. Geophys. Res. 104 (C11), 25937–25951.CrossRefGoogle Scholar
Jachec, S.M., Fringer, O.B., Street, R.L. & Gerritsen, M.G. 2007 Effects of grid resolution on the simulation of internal tides. Intl J. Offshore Polar Engng 17 (2), 432–438.Google Scholar
Kang, D. 2010 Energetics and dynamics of internal tides in monterey bay using numerical simulations a dissertation submitted to the department of civil and environmental engineering and the committee on graduate studies of Stanford University in partial fulfillment of. PhD thesis, Stanford university.Google Scholar
Kang, D. & Fringer, O. 2010 On the calculation of available potential energy in internal wave fields. J. Phys. Oceanogr. 40 (11), 2539–2545.CrossRefGoogle Scholar
Kang, D. & Fringer, O. 2012 Energetics of barotropic and baroclinic tides in the Monterey Bay area. J. Phys. Oceanogr. 42 (2), 272–290.CrossRefGoogle Scholar
Kelly, S.M. & Nash, J.D. 2010 Internal-tide generation and destruction by shoaling internal tides. Geophys. Res. Lett. 37 (23), L23611.CrossRefGoogle Scholar
Kelly, S.M., Nash, J.D. & Kunze, E. 2010 Internal-tide energy over topography. J. Geophys. Res. 115 (6), C06014.CrossRefGoogle Scholar
Klymak, J.M., Moum, J.N., Nash, J.D., Kunze, E., Girton, J.B., Carter, G.S., Lee, C.M., Sanford, T.B. & Gregg, M.C. 2006 An estimate of tidal energy lost to turbulence at the Hawaiian ridge. J. Phys. Oceanogr. 36 (6), 1148–1164.CrossRefGoogle Scholar
Kunze, E., Rosenfeld, L.K., Carter, G.S. & Gregg, M.C. 2002 Internal waves in Monterey Submarine Canyon. J. Phys. Oceanogr. 32 (6), 1890–1913.2.0.CO;2>CrossRefGoogle Scholar
Kurapov, A.L., Egbert, G.D., Allen, J.S., Miller, R.N., Erofeeva, S.Y. & Kosro, P.M. 2003 The M2 internal tide off Oregon: inferences from data assimilation. J. Phys. Oceanogr. 33 (8), 1733–1757.CrossRefGoogle Scholar
Lamb, K.G. 2007 Energy and pseudoenergy flux in the internal wave field generated by tidal flow over topography. Cont. Shelf Res. 27 (9), 1208–1232.CrossRefGoogle Scholar
Lien, R.-C., Henyey, F., Ma, B. & Yang, Y.J. 2014 Large-amplitude internal solitary waves observed in the Northern South China Sea: properties and energetics. J. Phys. Oceanogr. 44 (4), 1095–1115.CrossRefGoogle Scholar
Llewellyn, S., Stefan, G. & Young, W.R. 2002 Conversion of the barotropic tide. J. Phys. Oceanogr. 32 (5), 1554–1566.2.0.CO;2>CrossRefGoogle Scholar
Lorenz, E.N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7 (2), 157–167.CrossRefGoogle Scholar
Lu, Y., Wright, D.G. & Brickman, D. 2001 Internal tide generation over topography: experiments with a free-surface z-level ocean model. J. Atmos. Ocean. Technol. 18 (6), 1076–1091.2.0.CO;2>CrossRefGoogle Scholar
Maas, L.R.M. 2011 Topographies lacking tidal conversion. J. Fluid Mech. 684, 5–24.CrossRefGoogle Scholar
MacCready, P. & Giddings, S.N. 2016 The mechanical energy budget of a regional ocean model. J. Phys. Oceanogr. 46 (9), 2719–2733.CrossRefGoogle Scholar
Mellor, G.L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 20 (4), 851–875.CrossRefGoogle Scholar
Merrifield, M.A. & Holloway, P.E. 2002 Model estimates of M2 internal tide energetics at the Hawaiian Ridge. J. Geophys. Res. 107 (C8), 3179.CrossRefGoogle Scholar
Merrifield, M.A., Holloway, P.E. & Johnston, T.M.S. 2001 The generation of internal tides at the Hawaiian ridge. Geophys. Res. Lett. 28 (4), 559–562.CrossRefGoogle Scholar
Moum, J.N., Klymak, J.M., Nash, J.D., Perlin, A. & Smyth, W.D. 2007 Energy transport by nonlinear internal waves. J. Phys. Oceanogr. 37 (7), 1968–1988.CrossRefGoogle Scholar
Müller, M. 2013 On the space-and time-dependence of barotropic-to-baroclinic tidal energy conversion. Ocean Model. 72, 242–252.CrossRefGoogle Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes II: energetics of tidal and wind mixing. Deep-Sea Res. I 45 (12), 1977–2010.CrossRefGoogle Scholar
Nash, J.D., Shroyer, E.L., Kelly, S.M., Inall, M.E., Duda, T.F., Levine, M.D., Jones, N.L. & Musgrave, R.C. 2012 Are any coastal internal tides predictable? Oceanography 25 (2), 80–95.CrossRefGoogle Scholar
Nelko, V., Saha, A. & Chua, V.P. 2014 On the tidally driven circulation in the South China Sea: modeling and analysis. Ocean Dyn. 64 (3), 413–428.CrossRefGoogle Scholar
Palmer, M.R., Stephenson, G.R., Inall, M.E., Balfour, C., Düsterhus, A. & Green, J.A.M. 2015 Turbulence and mixing by internal waves in the Celtic Sea determined from ocean glider microstructure measurements. J. Mar. Syst. 144, 57–69.CrossRefGoogle Scholar
Pickering, A., Alford, M., Nash, J., Rainville, L., Buijsman, M., Ko, D.S. & Lim, B. 2015 Structure and variability of internal tides in Luzon Strait. J. Phys. Oceanogr. 45 (6), 1574–1594.CrossRefGoogle Scholar
Pollmann, F., Nycander, J., Eden, C. & Olbers, D. 2019 Resolving the horizontal direction of internal tide generation. J. Fluid Mech. 864, 381–407.CrossRefGoogle Scholar
Rattray, M. Jr. 1960 On the coastal generation of internal tides. Tellus 12 (1), 54–62.CrossRefGoogle Scholar
Scotti, A., Beardsley, R. & Butman, B. 2006 On the interpretation of energy and energy fluxes of nonlinear internal waves: an example from Massachusetts Bay. J. Fluid Mech. 561, 103–112.CrossRefGoogle Scholar
Venayagamoorthy, S.K. & Fringer, O.B. 2005 Nonhydrostatic and nonlinear contributions to the energy flux budget in nonlinear internal waves. Geophys. Res. Lett. 32 (15), L15603.CrossRefGoogle Scholar
Winters, K.B., Lombard, P.N., Riley, J.J. & D'Asaro, E.A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.CrossRefGoogle Scholar
Xu, M. & Chua, V.P. 2016 A numerical study on circulation and volume transport in Singapore coastal waters. J. Hydro-Environ. Res. 12, 70–90.CrossRefGoogle Scholar
Zhang, Z., Fringer, O.B. & Ramp, S.R. 2011 Three-dimensional, nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the South China Sea. J. Geophys. Res. 116 (C5), C05022.CrossRefGoogle Scholar
Zilberman, N.V., Becker, J.M., Merrifield, M.A. & Carter, G.S. 2009 Model estimates of M2 internal tide generation over mid-Atlantic ridge topography. J. Phys. Oceanogr. 39 (10), 2635–2651.CrossRefGoogle Scholar
Zilberman, N.V., Merrifield, M.A., Carter, G.S., Luther, D.S., Levine, M.D. & Boyd, T.J. 2011 Incoherent nature of M2 internal tides at the Hawaiian ridge. J. Phys. Oceanogr. 41 (11), 2021–2036.CrossRefGoogle Scholar