Benjamin’s gravity current into an ambient fluid with an open surface in a channel of general cross-section

Abstract

We present the solution of the idealized steady-state gravity current of height 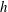$h$ and density 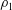$\unicode[STIX]{x1D70C}_{1}$ that propagates into an ambient motionless fluid of height 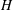$H$ and density 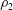$\unicode[STIX]{x1D70C}_{2}$ in a channel of general non-rectangular cross-section, with an upper surface open to the atmosphere, at high Reynolds number. The current propagates with speed 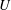$U$ and causes a depth decrease 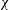$\unicode[STIX]{x1D712}$ of the top surface. This is a significant extension of Benjamin’s (J. Fluid Mech., vol. 31, 1968, pp. 209–248) seminal solution for the gravity current in a rectangular (or laterally unbounded) channel with a fixed top (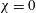$\unicode[STIX]{x1D712}=0$). The determination of 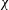$\unicode[STIX]{x1D712}$ is a part of the problem. Supposing that the direction of propagation is $x$ and gravity acceleration 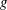$g$ acts in the 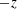$-z$ direction, the sidewalls are specified by 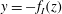$y=-f_{I}(z)$ and 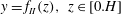$y=f_{II}(z),~z\in [0.H]$, and the width is 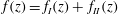$f(z)=f_{I}(z)+\,f_{II}(z)$. The dimensionless parameters of the problem are 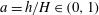$a=h/H\in (0,1)$ and 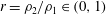$r=\unicode[STIX]{x1D70C}_{2}/\unicode[STIX]{x1D70C}_{1}\in (0,1)$. We show that a control-volume analysis of the type used by Benjamin produces a system of algebraic equations for 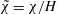$\tilde{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}/H$ and 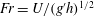$Fr=U/(g^{\prime }h)^{1/2}$ as functions of $a$ and $r$, where 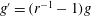$g^{\prime }=(r^{-1}-1)g$ is the reduced gravity. The geometry enters the equation via the width function 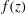$f(z)$. We present solutions for typical 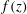$f(z)$: rectangle, semi-circle, 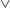$\vee$ triangle and trapezoid 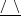$\text{}\underline{/~\backslash }$ . The results are physically acceptable and insightful. The non-negative dissipation condition defines the domain of validity 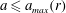$a\leqslant a_{max}(r)$ (also depending on 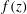$f(z)$); the equality sign corresponds to energy-conserving cases. The critical speed limitation (with respect to the characteristics) is also considered briefly and suggests a slightly smaller 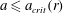$a\leqslant a_{crit}(r)$. The open-top results in the Boussinesq limit 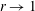$r\rightarrow 1$ coincide with the fixed-top solution. Upon the reduction of $r$, for a fixed thickness $a$, the value of 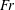$Fr$ decreases and 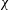$\unicode[STIX]{x1D712}$ increases, until the point of energy-conserving (non-dissipative) flow; for smaller $r$, a negative non-physical dissipation appears. The trends are more pronounced for a converging cross-section geometry (like 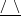$\text{}\underline{/~\backslash }$ ) than for the opposite shape (like 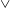$\vee$ triangle). The previously investigated Benjamin-type steady-state 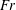$Fr$ and dissipation results are particular cases of the new formulation: 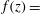$f(z)=$ const. reproduces the two-dimensional results, and 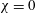$\unicode[STIX]{x1D712}=0$ recovers the fixed-top solution.