Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T06:30:31.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation and stability analysis of a jet in cross-flow: onset of global instability at a low velocity ratio

Published online by Cambridge University Press:  06 March 2012

Miloš Ilak ,
Philipp Schlatter ,
Shervin Bagheri  and
Dan S. Henningson
Miloš Ilak*
Affiliation:
Linné FLOW Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
Philipp Schlatter
Affiliation:
Linné FLOW Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
Shervin Bagheri
Affiliation:
Linné FLOW Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
Dan S. Henningson
Affiliation:
Linné FLOW Centre, Department of Mechanics, Royal Institute of Technology (KTH), SE-10044 Stockholm, Sweden
*
†Email address for correspondence: ilakm@utrc.utc.com
Get access Rights & Permissions [Opens in a new window]

Abstract

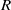We study direct numerical simulations (DNS) of a jet in cross-flow at low values of the jet-to-cross-flow velocity ratio . We observe that, as the ratio 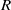increases, the flow evolves from simple periodic vortex shedding (a limit cycle) to more complicated quasi-periodic behaviour, before finally becoming turbulent, as seen in the simulation of Bagheri et al. (J. Fluid. Mech., vol. 624, 2009b, pp. 33–44). The value of 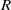at which the first bifurcation occurs for our numerical set-up is found, and shedding of hairpin vortices characteristic of a shear layer instability is observed. We focus on this first bifurcation, and find that a global linear stability analysis predicts well the frequency and initial growth rate of the nonlinear DNS at the critical value of 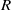and that good qualitative predictions about the dynamics can still be made at slightly higher values of 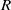where multiple unstable eigenmodes are present. In addition, we compute the adjoint global eigenmodes, and find that the overlap of the direct and the adjoint eigenmode, also known as a ‘wavemaker’, provides evidence that the source of the first instability lies in the shear layer just downstream of the jet.

JFM classification

Instability: Absolute/convective instability Nonlinear Dynamical Systems: Bifurcation Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 94 - 121
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: United Technologies Research Center, 411 Silver Lane, MS 129-85, East Hartford, CT 06108, USA.

References

1. Acarlar, M. & Smith, C. 1987a A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
2. Acarlar, M. & Smith, C. 1987b A study of hairpin vortices in a laminar boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.CrossRefGoogle Scholar
3. Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.CrossRefGoogle Scholar
4. Alves, L., Kelly, R. E. & Karagozian, A. R. 2007 Local stability analysis of an inviscid transverse jet. J. Fluid Mech. 581, 401–418.CrossRefGoogle Scholar
5. Alves, L., Kelly, R. E. & Karagozian, A. R. 2008 Transverse-jet shear-layer instabilities. Part 2. Linear analysis for large jet-to-crossflow velocity ratio. J. Fluid Mech. 602, 383–401.CrossRefGoogle Scholar
6. Bagheri, S. 2010 Analysis and control of transitional shear flows using global modes. PhD thesis, Royal Institute of Technology.Google Scholar
7. Bagheri, S., Brandt, L. & Henningson, D. S. 2009a Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.CrossRefGoogle Scholar
8. Bagheri, S., Schlatter, P., Schmid, P. J. & Henningson, D. S. 2009b Global stability of a jet in cross-flow. J. Fluid Mech. 624, 33–44.CrossRefGoogle Scholar
9. Bertolotti, F., Herbert, T. & Spalart, P. 1992 Linear and nonlinear stability of the Blasius boundary layer. J. Fluid Mech. 242, 441–474.CrossRefGoogle Scholar
10. Blanchard, J., Brunet, Y. & Merlen, A. 1999 Influence of a counter rotating vortex pair on the stability of a jet in a cross flow: an experimental study by flow visualizations. Exp. Fluids 26, 63–74.CrossRefGoogle Scholar
11. Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S. 2007 SIMSON: a pseudo-spectral solver for incompressible boundary layer flows. Tech Rep. TRITA-MEK 2007:07. KTH Mechanics.Google Scholar
12. Chomaz, J. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
13. Coelho, S. L. V. & Hunt, J. C. R. 1989 The dynamics of the near field of strong jets in crossflows. J. Fluid Mech. 200, 95–120.CrossRefGoogle Scholar
14. Cortelezzi, L. & Karagozian, A. R. 2001 On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 446, 347–373.CrossRefGoogle Scholar
15. Davitian, J., Getsinger, D., Hendrickson, C. & Karagozian, A. R. 2010 Transition to global instability in transverse-jet shear layers. J. Fluid Mech. 661, 294–315.CrossRefGoogle Scholar
16. Fric, T. F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.CrossRefGoogle Scholar
17. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
18. Grout, R., Gruber, A., Yoo, C. & Chen, J. 2010 Direct numerical simulation of flame stabilization downstream of a transverse fuel jet in cross-flow. Proceedings of the Combustion Institute 33, 1629–1637.CrossRefGoogle Scholar
19. Hammond, D. & Redekopp, L. G. 1998 Local and global instability properties of separation bubbles. Eur. J. Mech. B/Fluids 17 (2), 145–164.CrossRefGoogle Scholar
20. Hill, D. C. 1992 A theoretical approach for analysing the restabilization of wakes. AIAA Paper 92-0067.CrossRefGoogle Scholar
21. Hill, D. C. 1995 Adjoint systems and their role in the receptivity problem for boundary layers. J. Fluid Mech. 292, 183–204.CrossRefGoogle Scholar
22. Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
23. Ilak, M., Schlatter, P., Bagheri, S., Chevalier, M. & Henningson, D. S. 2011 Stability of a jet in crossflow. Phys. Fluids 23, 091113.CrossRefGoogle Scholar
24. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
25. Jovanović, M. B. 2006 Film cooling through imperfect holes. PhD thesis, Eindhoven University of Technology.Google Scholar
26. Karagozian, A. 2010 Transverse jets and their control. Prog. Energy Combust. Sci. 30, 1–23.Google Scholar
27. Kelso, R. M., Lim, T. T. & Perry, A. E. 1996 An experimental study of round jets in cross-flow. J. Fluid Mech. 306, 111–144.CrossRefGoogle Scholar
28. Kelso, R. M. & Smits, A. J. 1995 Horseshoe vortex systems resulting from the interaction between a laminar boundary layer and a transverse jet. Phys. Fluids 7 (1).CrossRefGoogle Scholar
29. Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users’ Guide. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
30. Li, Q., Schlatter, P. & Henningson, D. S. 2008 Spectral simulations of wall-bounded flows on massively parallel computers. Tech Rep. KTH Mechanics.Google Scholar
31. Lim, T. T., New, T. H. & Luo, S. C. 2001 On the development of large-scale structures of a jet normal to a cross flow. Phys. Fluids 13 (3), 770–775.CrossRefGoogle Scholar
32. Luchini, P., Giannetti, F. & Pralits, J. O. 2008 Structural sensitivity of linear and nonlinear global modes. AIAA Paper 2008-4227.CrossRefGoogle Scholar
33. Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
34. M’Closkey, R. T., King, J. M., Cortelezzi, L. & Karagozian, A. 2002 The actively controlled jet in crossflow. J. Fluid Mech. 452.CrossRefGoogle Scholar
35. Megerian, S., Davitian, J., Alves, L. S. d. B. & Karagozian, A. R. 2007 Transverse-jet shear-layer instabilities. Part 1. Experimental studies. J. Fluid Mech. 593, 93–129.CrossRefGoogle Scholar
36. Muldoon, F. & Acharya, S. 2010 Direct numerical simulation of pulsed jets-in-crossflow. Comput. Fluids 39, 1745–1773.CrossRefGoogle Scholar
37. Muppidi, S. & Mahesh, K. 2005 Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid Mech. 530, 81–100.CrossRefGoogle Scholar
38. Muppidi, S. & Mahesh, K. 2006 Two-dimensional model problem to explain counter-rotating vortex pair formation in a transverse jet. Phys. Fluids 18, 085103.CrossRefGoogle Scholar
39. Muppidi, S. & Mahesh, K. 2007 Direct numerical simulation of round turbulent jets in crossflow. J. Fluid Mech. 574, 59–84.CrossRefGoogle Scholar
40. Noack, B., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
41. Perry, A. E. & Lim, T. T. 1978 Coherent structures in coflowing jets and wakes. J. Fluid Mech. 88, 451–463.CrossRefGoogle Scholar
42. Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.CrossRefGoogle Scholar
43. Pier, B. 2008 Local and global instabilities in the wake of a sphere. J. Fluid Mech. 603, 39–61.CrossRefGoogle Scholar
44. Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
45. Rodriguez, D. & Theofilis, V. 2010 Structural changes of laminar separation bubbles induced by global linear instability. J. Fluid Mech. 655, 280–305.CrossRefGoogle Scholar
46. Salewski, M., Stankovic, D. & Fuchs, L. 2008 Mixing in circular and non-circular jets in crossflow. Flow Turbul. Combust. 80, 255–283.CrossRefGoogle Scholar
47. Schlatter, P., Bagheri, S. & Henningson, D. S. 2011 Self-sustained global oscillations of a jet in crossflow. Theor. Comput. Fluid Dyn. 25, 129–146.CrossRefGoogle Scholar
48. Smith, S. H. & Mungal, M. G. 1998 Mixing, structure and scaling of the jet in crossflow. J. Fluid Mech. 357, 83–122.CrossRefGoogle Scholar
49. Tammisola, O., Lundell, F., Schlatter, P., Wehrfritz, A. & Söderberg, L. D. 2011 Global linear and nonlinear stability of viscous confined plane wakes with co-flow. J. Fluid Mech. 675, 397–434.CrossRefGoogle Scholar
50. Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aeronaut. Sci. 39, 249–315.CrossRefGoogle Scholar
51. Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
52. Theofilis, V., Hein, S. & Dallmann, U. 2000 On the origins of unsteadiness and three-dimensionality in a laminar separation bubble. Phil. Trans. R. Soc. Lond. A 358, 3229–3246.CrossRefGoogle Scholar
53. Yuan, L. L., Street, R. L. & Ferziger, J. H. 1999 Large-eddy simulations of a round jet in crossflow. J. Fluid Mech. 379, 71–104.CrossRefGoogle Scholar
54. Ziefle, J. 2007 Large-eddy simulation of complex massively-separated turbulent flows. PhD thesis, ETH Zurich, Diss. no. 17846.Google Scholar
55. Ziefle, J. & Kleiser, L. 2009 Large-eddy simulation of a round jet in crossflow. AIAA J. 47 (5), 1158–1172.CrossRefGoogle Scholar