Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T11:15:17.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Blood flow in the choriocapillaris

Published online by Cambridge University Press:  02 June 2015

M. A. Zouache ,
I. Eames  and
P. J. Luthert
M. A. Zouache*
Affiliation:
Institute of Ophthalmology, University College London, 11-43 Bath Street, London EC1V 9EL, UK
I. Eames
Affiliation:
Department of Mechanical Engineering, University College London, Torrington Place, London WC1E 7JE, UK
P. J. Luthert
Affiliation:
Institute of Ophthalmology, University College London, 11-43 Bath Street, London EC1V 9EL, UK
*
†Email address for correspondence: moussa.zouache.10@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The choriocapillaris is a capillary bed located in a thin layer adjacent to the outer retina and is part of the oxygen delivery system to the photoreceptors of the eye. The blood flow is approximately planar and is serviced by microvessels, which join the choriocapillaris through inlets perpendicular to its plane. Capillaries are densely organised and separated by avascular septal posts, which direct the blood flow. The capillary bed is composed of a juxtaposition of tessellating vascular units called lobules, which are filled and drained independently from each other. A theoretical analysis of the blood flow in an idealised model of a lobule of the choriocapillaris is developed and studied. Lobules are modelled as tessellating polygonal prisms, where the upper and lower surfaces correspond to planar parallel membranes. The septae are modelled as cylinders randomly distributed between the two membranes. Feeding arterioles and draining venules are modelled as inlets and outlets connecting at the lower surface of the prism perpendicularly to the plane of the lobule. An inlet is placed inside the lobule, while an outlet is placed at each of the vertices. The polygonal prism can be formally subdivided into a set of triangular prisms with one inlet and two outlets, each of them located at one of the vertices. The triangular prisms are taken to be isosceles, and are therefore characterised by a vertex angle 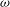${\it\omega}$ at the inlet and a span $L$. The flow is viscously dominated, and is investigated in the lubrication limit, in which the characteristic thickness of the prism is much smaller than the diameter of the cylinders. As a result of the geometry, a stagnation point is located midway between the outlets. A separation streamline joins the inlet and the stagnation point. The pressure drop 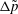${\rm\Delta}\tilde{p}$ and the average fluid particle residence time 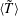$\langle \tilde{T}\rangle$ are analysed as a function of the angle at the inlet 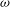${\it\omega}$ and the septae volume fraction 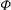${\it\Phi}$. When no cylinders are present (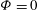${\it\Phi}=0$), an analytical expression for the pressure field is calculated by conformal mapping. Close to the triangle walls, the flow is quasi-parallel and characterised by a shorter fluid particle residence time. In the vicinity of the stagnation point, the velocity decreases and the residence time diverges logarithmically with the distance to the stagnation streamline. The minimum in pressure drop corresponds to a maximum in residence time, and is obtained for 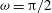${\it\omega}={\rm\pi}/2$. Asymptotic expressions for the pressure drop and average residence time are formulated in both the limits 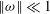$\Vert {\it\omega}\Vert \ll 1$ and 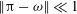$\Vert {\rm\pi}-{\it\omega}\Vert \ll 1$. The impact of 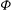${\it\Phi}$ on the flow is characterised by solving the equations for the flow numerically and using the Darwin drift framework. 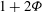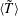We show that the pressure drop is approximately proportional to $1+2{\it\Phi}$ for relatively small ${\it\Phi}$, and that $\langle \tilde{T}\rangle$ is proportional to 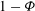$1-{\it\Phi}$ regardless of the void fraction or shape of the septae. In the case 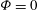${\it\Phi}=0$, the average residence time equals the volume of the domain divided by the volumetric flux. This analysis provides a new perspective on the blood flow dynamics within the choriocapillaris. Lobules form systems, where perfusion and corpuscle transport are a function of the angle that any two venular openings make with an arteriolar opening, the surface area perfused and the void volume fraction. The blood flow velocity and residence time are significantly heterogeneous, which may be responsible for the high degree of selective localisation observed in the pathogenesis of some inflammatory and degenerative diseases of the eye.

JFM classification

Biological Fluid Dynamics: Blood flow Low-Reynolds-number flows: Hele-Shaw flows Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , pp. 37 - 66
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A.(Eds) 1972 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, 9th printing, Dover.Google Scholar
Aiello, L. P., Northrup, J. M., Keyt, B. A., Takagi, H. & Iwamoto, M. A. 1995 Hypoxic regulation of vascular endothelial growth factor in retinal cells. Arch. Ophthalmol. 113 (12), 1538–1544.CrossRefGoogle ScholarPubMed
Amalric, P. 1983 The choriocapillaris in the macular area: clinical and angiographic study. Intl Ophthalmol. 6, 149–153.CrossRefGoogle ScholarPubMed
Armaly, M. F. & Araki, M. 1974 Effect of ocular pressure on choroidal circulation in the cat and rhesus monkey. Invest. Ophthalmol. Vis. Sci. 14 (8), 584–591.Google Scholar
Balsa, T. F. 1998 Secondary flow in a Hele-Shaw cell. J. Fluid Mech. 372, 25–44.CrossRefGoogle Scholar
Benjamin, T. B. 1986 Note on added mass and drift. J. Fluid Mech. 169, 251–256.Google Scholar
Bill, A. 1962 Intraocular pressure and blood flow through the uvea. Arch. Ophthalmol. 67, 336–348.CrossRefGoogle ScholarPubMed
Braun, R. D., Dewhirst, M. W. & Hatchell, D. L. 1997 Quantification of the erythrocyte flow in the choroid of the albino rat. Am. J. Physiol. 272, H1444–H1453.Google Scholar
Bunce, C., Xing, W. & Wormald, R. 2010 Causes of blind and partial sight certifications in England and Wales: April 2007–March 2008. Eye 24 (11), 1692–1699.Google Scholar
Ciulla, T. A., Harris, A., Chung, H. S., Danis, R. P., Kagemann, L., McNulty, L., Pratt, L. M. & Martin, B. J. 1999 Color Doppler imaging discloses reduced ocular blood flow velocities in nonexudative age-related macular degeneration. Am. J. Ophthalmol. 128, 75–80.Google Scholar
Condren, A. B., Kumar, A., Mettu, P., Liang, K. J., Zhao, L., Yue Tsai, J., Fariss, R. N. & Wong, W. T. 2013 Perivascular mural cells of the mouse choroid demonstrate morphological diversity that is correlated to vasoregulatory function. PLoS ONE 8 (1), e53386.CrossRefGoogle ScholarPubMed
Curcio, C. A., Messinger, J. D., Sloan, K. R., Mitra, A., McGwin, G. & Spaide, R. F. 2011 Human chorioretinal layer thicknesses measured in macula-wide, high-resolution histologic sections. Invest. Ophthalmol. Vis. Sci. 52 (7), 3943–3954.Google Scholar
Darwin, C. 1953 Note on hydrodynamics. Math. Proc. Camb. Phil. Soc. 49 (2), 342–354.Google Scholar
Dorey, C. K., Aouididi, S., Reynaud, X., Dvorak, H. F. & Brown, L. F. 1996 Correlation of vascular permeability factor/vascular endothelial growth factor with extraretinal neovascularization in the rat. Arch. Ophthalmol. 114 (10), 1210–1217.Google Scholar
Eames, I., Belcher, S. E. & Hunt, J. C. R. 1994 Drift, partial drift and Darwin’s proposition. J. Fluid Mech. 275, 201–223.Google Scholar
Eames, I. & Bush, J. W. M. 1999 Longitudinal dispersion by bodies fixed in a potential flow. Proc. R. Soc. Lond. A 455, 3665–3686.Google Scholar
Eames, I., Hunt, J. C. R. & Belcher, S. E. 2004 Inviscid mean flow through and around groups of bodies. J. Fluid Mech. 515, 371–389.Google Scholar
Fahraeus, R. 1929 The suspension stability of the blood. Physiol. Rev. 9 (2), 241–274.CrossRefGoogle Scholar
Flower, R. W., Fryczkowski, A. W. & McLeod, D. S. 1995 Variability in choriocapillaris blood flow distribution. Invest. Ophthalmol. Vis. Sci. 36 (7), 1247–1258.Google Scholar
Flower, R. W., von Kerczek, C., Zhu, L., Ernest, A., Eggleton, C. & Topoleski, L. D. 2001 Theoretical investigation of the role of choriocapillaris blood flow in treatment of subfoveal choroidal neovascularization associated with age-related macular degeneration. Am. J. Ophthalmol. 132 (1), 85–93.CrossRefGoogle ScholarPubMed
Friedman, E. 1970 Choroidal blood flow. Pressure–flow relationships. Arch. Ophthalmol. 83, 95–99.Google Scholar
Friedman, E., Smith, T. R. & Kuwabara, T. 1963 Senile choroidal patterns and drusen. Arch. Ophthalmol. 69, 114–124.CrossRefGoogle ScholarPubMed
Fryczkowski, A. W. 1994 Anatomical and functional choroidal lobuli. Intl Ophthalmol. 18, 131–141.Google Scholar
Fryczkowski, A. W., Grimson, B. S. & Peiffer, R. L. 1985 Vascular casting and scanning electron microscopy of human ocular vascular abnormalities. Arch. Ophthalmol. 103, 118–120.CrossRefGoogle ScholarPubMed
Fryczkowski, A. W. & Sherman, M. D. 1988 Scanning electron microscopy of human ocular vascular casts: the submacular choriocapillaris. Acta Anat. 132, 265–269.CrossRefGoogle ScholarPubMed
Fryczkowski, A. W., Sherman, M. D. & Walker, J. 1991 Observations on the lobular organization of the human choriocapillaris. Intl Ophthalmol. 15, 109–120.CrossRefGoogle ScholarPubMed
Fujiwara, T., Iida, T. & Kanda, N. 2007 Lobular structure of the choriocapillaris in a patient with ophthalmic artery occlusion. Japan. J. Ophthalmol. 51, 477–481.CrossRefGoogle Scholar
Garron, L. K. 1963 The ultrastructure of the retinal pigment epithelium with observations on the choriocapillaris and Bruch’s membrane. Trans. Am. Ophthalmol. Soc. 61, 545–588.Google ScholarPubMed
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.Google Scholar
Gherezguiher, T., Okubo, H. & Koss, M. C. 1991 Choroidal and ciliary body blood flow analysis: application of laser Doppler flowmetry in experimental animals. Exp. Eye Res. 53, 151–156.Google Scholar
Hayreh, S. S. 1974a The choriocapillaris. A. Graef. Arch. Klin. Ex. 192, 165–179.CrossRefGoogle ScholarPubMed
Hayreh, S. S. 1974b Recent advances in fluorescein fundus angiography. Brit. J. Ophthalmol. 58 (4), 391–412.CrossRefGoogle ScholarPubMed
Hayreh, S. S. 1975 Segmental nature of the choroidal vasculature. Brit. J. Ophthalmol. 59, 631–648.Google Scholar
Hele-Shaw, H. S. 1898 The flow of water. Nature 58 (1489), 34–36.CrossRefGoogle Scholar
Hirata, Y., Nishiwaki, H., Miura, S., Ieki, Y., Honda, Y., Yumikake, K., Sugino, Y. & Okazaki, Y. 2004 Analysis of choriocapillaris flow patterns by continuous laser-targeted angiography in monkeys. Invest. Ophthalmol. Vis. Sci. 45 (6), 1954–1962.CrossRefGoogle ScholarPubMed
Hogan, M. J., Alvarado, J. A. & Weddell, J. E. 1971 Histology of the Human Eye: An Atlas and Textbook. Saunders.Google Scholar
Hogan, M. J. & Feeney, L. 1961 Electron-microscopy of the human choroid. Am. J. Ophthalmol. 51 (5), 1084–1097.Google Scholar
Hunt, J. C. R., Abell, C. J., Peterka, J. A. & Woo, H. 1978 Kinematical studies of the flows around free or surgace-mounted obstacles; applying topology to flow visualization. J. Fluid Mech. 86 (1), 179–200.CrossRefGoogle Scholar
Inoue, Y., Yanagi, Y., Matsuura, K., Takahashi, H., Tamaki, Y. & Araie, M. 2007 Expression of hypoxia-inducible factor 1 ${\it\alpha}$ and 2 ${\it\alpha}$ in choroidal neovascular membranes associated with age-related macular degeneration. Brit. J. Ophthalmol. 91 (12), 1720–1721.Google Scholar
Klien, B. A. 1966 Regional and aging characteristics of the normal choriocapillaris in flat preparations. Am. J. Ophthalmol. 61 (5), 1191–1197.CrossRefGoogle ScholarPubMed
Lee, J. S. & Fung, Y. C. 1969 Stokes flow around a circular cylindrical post confined between two parallel plates. J. Fluid Mech. 37, 657–670.CrossRefGoogle Scholar
Lighthill, M. J. 1956 Drift. J. Fluid Mech. 1 (1), 31–53.Google Scholar
Mäepa, O. 1992 Pressure in the anterior ciliary arteries, choroidal veins and choriocapillaris. Exp. Eye Res. 54, 731–736.Google Scholar
Mendrinos, E. & Pournaras, C. J. 2009 Topographic variation of the choroidal watershed zone and its relationship to neovascularization in patients with age-related macular degeneration. Acta Ophthalmol. 87, 290–296.CrossRefGoogle ScholarPubMed
Moser, M., Schneditz, D., Gallash, E. & Kenner, T.1988 Investigation of pulmonary and coronary microvascular properties by blood density measurements. Proc. Symp. Frontiers Cardiopulm. Mech. pp. 57, as quoted by Kenner, T. 1989. The measurement of blood density and its meaning. Basic Res. Cardiol. 84, 111–124.Google Scholar
Nehari, Z. 1952 Conformal Mapping. McGraw-Hill.Google Scholar
Paterson, L. 1981 Radial fingering in a Hele-Shaw cell. J. Fluid Mech. 113, 513–529.Google Scholar
Pauleikhoff, D., Spital, G., Radermacher, M., Brumm, G. A., Lommatzsh, A. & Bird, A. C. 1999 A fluorescein and indocynanine green angiographic study of choriocapillaris in age-related macular degeneration. Arch. Ophthalmol. 117, 1353–1358.CrossRefGoogle Scholar
Pries, A. R., Secomb, T. W., Gessner, T., Sperandio, M. B., Gross, J. F. & Gaehtgens, P. 1994 Resistence to blood flow in microvessels in vivo. Circulat. Res 75, 904–915.CrossRefGoogle ScholarPubMed
Ramrattan, R. S., van der Schaft, T. L., Mooy, C. M., de Bruijn, W. C., Mulder, P. G. H. & de Jong, P. T. V. M. 1994 Morphometric analysis of Bruch’s membrane, the choriocapillaris and the choroid in aging. Invest. Ophthalmol. Vis. Sci. 35 (6), 2857–2864.Google Scholar
Replogle, R. L., Meiselman, H. J. & Merrill, E. W. 1967 Clinical implications of blood rheology studies. Circulation 36, 148–160.Google Scholar
Reynolds, O. 1886 On the theory of lubrication and its application to Mr. Beauchamp Tower’s experiment, including an experimental determination of the viscosity of olive oil. Phil. Trans. R. Soc. Lond. A 177, 157–235.Google Scholar
Richardson, S. 1972 Hele-Shaw flows with a free boundary produced by the injection of fluid into a narrow channel. J. Fluid Mech. 56, 609–618.Google Scholar
Salzman, M. 1912 The Anatomy and Histology of the Human Eyeball in the Normal State, its Development and Senescence. The University of Chicago Press; Trans by E. V. L. Brown.Google Scholar
Sheridan, C. M., Pate, S., Hiscott, P., Wong, D., Pattwell, D. M. & Kent, D. 2009 Expression of hypoxia-inducible factor-1 ${\it\alpha}$ and -2 ${\it\alpha}$ in human choroidal neovascular membranes. Graefes Arch. Clin. Exp. Ophthalmol. 247 (10), 1361–1367.CrossRefGoogle ScholarPubMed
Spraul, C. W., Lang, G. E., Grossniklaus, H. E. & Lang, G. K. 1999 Histologic and morphometric analysis of the choroid, Bruch’s membrane, and retinal pigment epithelium in postmortem eyes with age-related macular degeneration and histologic examination of surgically excised choroidal neovascular membranes. Surv. Ophthalmol. 44, S10–S32.Google Scholar
Spraul, C. W., Lang, G. E., Lang, G. K. & Grossniklaus, H. E. 2002 Morphometric changes of the choriocapillaris and the choroidal vasculature in eyes with advanced glaucomatous changes. Vis. Res. 42 (7), 923–932.Google Scholar
Stefansson, E., Geirsdottir, A. & Sigurdsson, H. 2011 Metabolic physiology in age-related macular degeneration. Prog. Retin. Eye Res. 30, 72–80.Google Scholar
Takasu, I., Shiraga, F., Okanouchi, T., Tsuchida, Y. & Ohtsuki, H. 2000 Evaluation of leukocyte dynamics in choroidal circulation with indocyanine green-stained leukocytes. Invest. Ophthalmol. Vis. Sci. 41, 2844–2848.Google ScholarPubMed
Thompson, B. W. 1968 Secondary flow in a Hele-Shaw cell. J. Fluid Mech. 31, 379–395.Google Scholar
Torczynski, E. & Tso, M. O. M. 1976 The architecture of the choriocapillaris at the posterior pole. Am. J. Ophthalmol. 81 (4), 428–440.Google Scholar
Tsay, R.-Y. & Weinbaum, S. 1991 Viscous flow in a channel with periodic cross-bridging fibres: exact solutions and Brinkman approximation. J. Fluid Mech. 226, 125–148.Google Scholar
Wei, H. H., Waters, S. L., Liu, S. Q. & Grotberg, J. B. 2003 Flow in a wavy-walled channel lined with a poroelastic layer. J. Fluid Mech. 492, 23–45.Google Scholar
Yih, C.-S. 1985 New derivations of Darwin’s theorem. J. Fluid Mech. 152, 163–172.Google Scholar
Yih, C.-S. 1997 Evolution of Darwinian drift. J. Fluid Mech. 347, 1–11.Google Scholar
Yoneya, S. & Tso, M. O. M. 1987 Angioarchitecture of the human choroid. Arch. Ophthalmol. 105 (5), 681–687.CrossRefGoogle ScholarPubMed
Yoneya, S., Tso, M. O. M. & Shimizu, K. 1983 Patterns of the choriocapillaris: a method to study the choroidal vasculature of the enucleated human eye. Intl Ophthalmol. 6, 95–99.CrossRefGoogle Scholar
Zang, H. R. 1994 Scanning electron-microscopic study of corrosion casts on retinal and choroidal angioarchitecture in man and animals. Prog. Retin. Eye Res. 13 (1), 243–270.CrossRefGoogle Scholar
Zheng, Y. & Weinbaum, S. 1994 Stokes flow through periodic orifices in a channel. J. Fluid Mech. 263, 207–226.Google Scholar
Zhu, L., Zheng, Y., von Kerczek, C. H., Topoleski, L. D. T. & Flower, R. W. 2006 Feasibility of extracting velocity distribution in choriocapillaris in human eyes from ICG dye angiograms. J. Biomed. Engng 128, 203–209.Google Scholar