Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T12:55:36.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristics of the turbulent energy dissipation rate in a cylinder wake

Published online by Cambridge University Press:  27 November 2017

J. G. Chen Open the ORCID record for J. G. Chen [Opens in a new window] ,
Y. Zhou ,
R. A. Antonia  and
T. M. Zhou
J. G. Chen
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen 518055, China School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Y. Zhou*
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen 518055, China
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
T. M. Zhou
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: yuzhou@hit.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

This work aims to improve our understanding of the turbulent energy dissipation rate in the wake of a circular cylinder. Ten of the twelve velocity derivative terms which make up the energy dissipation rate are simultaneously obtained with a probe composed of four X-wires. Measurements are made in the plane of mean shear at 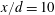$x/d=10$, 20 and 40, where $x$ is the streamwise distance from the cylinder axis and 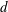$d$ is the cylinder diameter, at a Reynolds number of 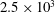$2.5\times 10^{3}$ based on 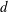$d$ and free-stream velocity. Both statistical and topological features of the velocity derivatives as well as the energy dissipation rate, approximated by a surrogate based on the assumption of homogeneity in the transverse plane, are examined. The spectra of the velocity derivatives indicate that local axisymmetry is first satisfied at higher wavenumbers while the departure at lower wavenumbers is caused by the Kármán vortex street. The spectral method proposed by Djenidi & Antonia (Exp. Fluids, vol. 53, 2012, pp. 1005–1013) based on the universality of the dissipation range of the longitudinal velocity spectrum normalized by the Kolmogorov scales also applies in the present flow despite the strong perturbation from the Kármán vortex street and violation of local isotropy at small 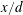$x/d$. The appropriateness of the spectral chart method is consistent with Antonia et al.’s (Phys. Fluids, vol. 26, 2014, 45105) observation that the two major assumptions in Kolmogorov’s first similarity hypothesis, i.e. very large Taylor microscale Reynolds number and local isotropy, can be significantly relaxed. The data also indicate that vorticity spectra are more sensitive, when testing the first similarity hypothesis, than velocity spectra. They also reveal that the velocity derivatives 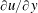$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$ and 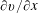$\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}x$ play an important role in the interaction between large and small scales in the present flow. The phase-averaged data indicate that the energy dissipation is concentrated mostly within the coherent spanwise vortex rollers, in contrast with the model of Hussain (J. Fluid Mech., vol. 173, 1986, pp. 303–356) and Hussain & Hayakawa (J. Fluid Mech., vol. 180, 1987, p. 193), who conjectured that it resides mainly in regions of strong turbulent mixing.

JFM classification

Turbulent Flows: Turbulent Flows Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 271 - 300
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Antonia, R., Orlandi, P. & Zhou, T. 2002 Assessment of a three-component vorticity probe in decaying turbulence. Exp. Fluids 33, 384–390.Google Scholar
Antonia, R. A. & Abe, H. 2009 Inertial range similarity for velocity and scalar spectra in a turbulent channel flow. In Proceedings of the Sixth International Symposium on Turbulence, Heat and Mass Transfer, Rome, Italy, Begell House.Google Scholar
Antonia, R. A., Anselmet, F. & Chambers, A. J. 1986 Assessment of local isotropy using measurements in a turbulent plane jet. J. Fluid Mech. 163, 365–391.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipative range on Kolmogorov scales. Phys. Fluids 26, 45105.CrossRefGoogle Scholar
Antonia, R. A., Kim, J. & Browne, L. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.CrossRefGoogle Scholar
Antonia, R. A. & Mi, J. 1998 Approach towards self-preservation of turbulent cylinder and screen wakes. Exp. Therm. Fluid Sci. 17, 277–284.Google Scholar
Antonia, R. A., Shafi, H. S. & Zhu, Y. 1996 A note on the vorticity spectrum. Phys. Fluids 8, 2196–2202.Google Scholar
Antonia, R. A., Shah, D. A. & Browne, L. W. B. 1988 Dissipation and vorticity spectra in a turbulent wake. Phys. Fluids 31, 1805–1807.CrossRefGoogle Scholar
Antonia, R. A., Zhu, Y. & Kim, J. 1993 On the measurement of lateral velocity derivatives in turbulent flows. Exp. Fluids 15, 65–69.Google Scholar
Browne, L., Antonia, R. A. & Shah, D. A. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.Google Scholar
Chapman, D. R. 1979 Computational aerodynamics development and outlook. AIAA J. 17, 1293–1313.CrossRefGoogle Scholar
Chen, J. G., Zhou, T. M., Antonia, R. A. & Zhou, Y. 2017 Comparison between passive scalar and velocity fields in a turbulent cylinder wake. J. Fluid Mech. 813, 667–694.Google Scholar
Chen, J. G., Zhou, Y., Zhou, T. M. & Antonia, R. A. 2016 Three-dimensional vorticity, momentum and heat transport in a turbulent cylinder wake. J. Fluid Mech. 809, 135–167.CrossRefGoogle Scholar
Djenidi, L. 2006 Lattice-Boltzmann simulation of grid-generated turbulence. J. Fluid Mech. 552, 13.Google Scholar
Djenidi, L. & Antonia, R. A. 2009 Momentum and heat transport in a three-dimensional transitional wake of a heated square cylinder. J. Fluid Mech. 640, 109–129.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2012 A spectral chart method for estimating the mean turbulent kinetic energy dissipation rate. Exp. Fluids 53, 1005–1013.CrossRefGoogle Scholar
Frisch, U. 1996 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
George, W. & Hussein, H. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.CrossRefGoogle Scholar
Gulitski, G., Kholmyansky, M., Kinzelbach, W., Lüthi, B., Tsinober, A. & Yorish, S. 2007 Velocity and temperature derivatives in high-Reynolds-number turbulent flows in the atmospheric surface layer. Part 1. Facilities, methods and some general results. J. Fluid Mech. 589, 57–81.Google Scholar
Huang, J. F., Zhou, Y. & Zhou, T. 2006 Three-dimensional wake structure measurement using a modified PIV technique. Exp. Fluids 40, 884–896.Google Scholar
Hussain, A. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Hussain, A. K. M. F. 1983 Coherent structures – reality and myth. Phys. Fluids 26, 2816–2850.Google Scholar
Hussain, A. K. M. F. & Hayakawa, M. 1987 Eduction of large-scale organized structures in a turbulent plane wake. J. Fluid Mech. 180, 193–229.CrossRefGoogle Scholar
Hussein, H. J. 1994 Evidence of local axisymmetry in the small scales of a turbulent planar jet. Phys. Fluids 6, 2058–2070.CrossRefGoogle Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kim, J. & Antonia, R. A. 1993 Isotropy of the small scales of turbulence at low Reynolds number. J. Fluid Mech. 251, 219–238.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Landau, L. D. & Lifschitz, E. M. 1987 Fluid Mechanics. Butterworth Heinemann.Google Scholar
Lefeuvre, N., Thiesset, F., Djenidi, L. & Antonia, R. A. 2014 Statistics of the turbulent kinetic energy dissipation rate and its surrogates in a square cylinder wake flow. Phys. Fluids 26, 95104.Google Scholar
Mi, J. & Antonia, R. A. 2010 Approach to local axisymmetry in a turbulent cylinder wake. Exp. Fluids 48, 933–947.CrossRefGoogle Scholar
Mohamed, M. S. & Larue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rogers, M. M. & Moin, P. 1987 Helicity fluctuations in incompressible turbulent flows. Phys. Fluids 30, 2662–2671.Google Scholar
Saarenrinne, P. & Piirto, M. 2000 Turbulent kinetic energy dissipation rate estimation from PIV velocity vector fields. Exp. Fluids 29, S300–S307.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Shafi, H. S. & Antonia, R. A. 1997 Small-scale characteristics of a turbulent boundary layer over a rough wall. J. Fluid Mech. 342, 263–293.CrossRefGoogle Scholar
She, Z.-S., Chen, S., Doolen, G., Kraichnan, R. H. & Orszag, S. A. 1993 Reynolds number dependence of isotropic Navier–Stokes turbulence. Phys. Rev. Lett. 70, 3251–3254.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344, 226–228.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015 Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thiesset, F., Danaila, L. & Antonia, R. A. 2013 Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake. J. Fluid Mech. 720, 393–423.Google Scholar
Thiesset, F., Danaila, L. & Antonia, R. A. 2014 Dynamical interactions between the coherent motion and small scales in a cylinder wake. J. Fluid Mech. 749, 201–226.CrossRefGoogle Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Wallace, J. M. 2009 Twenty years of experimental and direct numerical simulation access to the velocity gradient tensor: what have we learned about turbulence? Phys. Fluids 21, 21301.CrossRefGoogle Scholar
Wallace, J. M. & Foss, J. F. 1995 The measurement of vorticity in turbulent flows. Annu. Rev. Fluid Mech. 27, 469–514.Google Scholar
Yiu, M. W., Zhou, Y., Zhou, T. & Cheng, L. 2004 Reynolds number effects on three-dimensional vorticity in a turbulent wake. AIAA J. 42, 1009–1016.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders. Oxford University Press.CrossRefGoogle Scholar
Zhou, T. & Antonia, R. A. 1992 Convection velocity measurements in a cylinder wake. Exp. Fluids 13, 63–70.CrossRefGoogle Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.CrossRefGoogle Scholar
Zhou, T., Antonia, R. A., Lasserre, J. J., Coantic, M. & Anselmet, F. 2003a Transverse velocity and temperature derivative measurements in grid turbulence. Exp. Fluids 34, 449–459.Google Scholar
Zhou, T., Pearson, B. R. & Antonia, R. A. 2001 Comparison between temporal and spatial transverse velocity increments in a turbulent plane jet. Fluid Dyn. Res. 28, 127–138.Google Scholar
Zhou, T., Razali, S. M., Zhou, Y., Chua, L. P. & Cheng, L. 2009 Dependence of the wake on inclination of a stationary cylinder. Exp. Fluids 46, 1125–1138.CrossRefGoogle Scholar
Zhou, T., Zhou, Y., Yiu, M. W. & Chua, L. P. 2003b Three-dimensional vorticity in a turbulent cylinder wake. Exp. Fluids 35, 459–471.Google Scholar
Zhou, Y. & Antonia, R. A. 1995 Memory effects in a turbulent plane wake. Exp. Fluids 19, 112–120.Google Scholar
Zhu, Y. & Antonia, R. A. 1996a On the correlation between enstrophy and energy dissipation rate in a turbulent wake. Appl. Sci. Res. 57, 337–347.Google Scholar
Zhu, Y. & Antonia, R. A. 1996b Spatial resolution of a 4-X-wire vorticity probe. Meas. Sci. Technol. 7, 1492–1497.CrossRefGoogle Scholar
Zhu, Y. & Antonia, R. A. 1996c The spatial resolution of hot-wire arrays for the measurement of small-scale turbulence. Meas. Sci. Technol. 7, 1349–1359.Google Scholar