Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Åström, J. A.
Carter, A.
Hetherington, J.
Ioakimidis, K.
Lindahl, E.
Mozdzynski, G.
Nash, R. W.
Schlatter, P.
Signell, A.
and
Westerholm, J.
2013.
Applied Parallel and Scientific Computing.
Vol. 7782,
Issue. ,
p.
27.
Gross, Andreas
and
Fasel, Hermann
2013.
Numerical Investigation of Flows with Three-Dimensional Separation.
Sayles, Emily L.
and
Eaton, John K.
2014.
Sensitivity of an asymmetric, three-dimensional diffuser to inlet condition perturbations.
International Journal of Heat and Fluid Flow,
Vol. 49,
Issue. ,
p.
100.
Duquesne, P
Maciel, Y
Ciocan, G D
and
Deschênes, C
2014.
Flow separation in a straight draft tube, particle image velocimetry.
IOP Conference Series: Earth and Environmental Science,
Vol. 22,
Issue. 3,
p.
032004.
Duquesne, P
Maciel, Y
Aeschlimann, V
Ciocan, G D
and
Deschênes, C
2014.
Power break off in a bulb turbine: wall pressure sensor investigation.
IOP Conference Series: Earth and Environmental Science,
Vol. 22,
Issue. 3,
p.
032014.
Duquesne, Pierre
Maciel, Yvan
and
Deschênes, Claire
2015.
Unsteady flow separation in a turbine diffuser.
Experiments in Fluids,
Vol. 56,
Issue. 8,
Maden, I.
Maduta, R.
Kriegseis, J.
Jakirlic, S.
Grundmann, S.
and
Tropea, C.
2015.
Plasma-actuated Manipulation of Secondary Flow Towards Pressure Recovery Enhancement in a 3D Diffuser Modelled by an Eddy-resolving Second-moment Closure.
Flow, Turbulence and Combustion,
Vol. 95,
Issue. 2-3,
p.
377.
Duquesne, Pierre
Maciel, Yvan
and
Deschênes, Claire
2016.
Investigation of Flow Separation in a Diffuser of a Bulb Turbine.
Journal of Fluids Engineering,
Vol. 138,
Issue. 1,
Lu, Lipeng
Zhong, Luyang
and
Liu, Yangwei
2016.
Turbulence models assessment for separated flows in a rectangular asymmetric three-dimensional diffuser.
Engineering Computations,
Vol. 33,
Issue. 4,
p.
978.
Mohammed-Taifour, Abdelouahab
and
Weiss, Julien
2016.
Unsteadiness in a large turbulent separation bubble.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
p.
383.
Zhang, Meihua
and
Zheng, Zhongquan C.
2018.
Relations of POD modes and Lyapunov exponents to the nonlinear dynamic states in flow over oscillating tandem cylinders.
Physics of Fluids,
Vol. 30,
Issue. 12,
p.
123602.
Xu, Hui
Cantwell, Chris D.
Monteserin, Carlos
Eskilsson, Claes
Engsig-Karup, Allan P.
and
Sherwin, Spencer J.
2018.
Spectral/hp element methods: Recent developments, applications, and perspectives.
Journal of Hydrodynamics,
Vol. 30,
Issue. 1,
p.
1.
Elyasi, Mohammad
and
Ghaemi, Sina
2019.
Experimental investigation of coherent structures of a three-dimensional separated turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
1.
Das, Prashant
and
Ghaemi, Sina
2020.
Volumetric measurement of turbulence and flow topology in an asymmetric diffuser.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Zhang, Zheying
Zhang, Wei
and
Zhu, Zuchao
2022.
Transient separation and fluctuation of turbulent flow in an axisymmetric U-turn channel perturbed by periodically passing gust inflow.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 236,
Issue. 14,
p.
7745.
Hajaali, Arthur
and
Stoesser, Thorsten
2022.
Flow Separation Dynamics in Three-Dimensional Asymmetric Diffusers.
Flow, Turbulence and Combustion,
Vol. 108,
Issue. 4,
p.
973.
Zhang, Zheying
Zhang, Wei
and
Zhu, Zuchao
2022.
Numerical investigation on separated turbulent flow in a three-dimensional U-turn duct with spanwise diverging.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 236,
Issue. 5,
p.
2268.
Buron, Jean-David
and
Houde, Sébastien
2023.
Modal decomposition of flow instabilities in a straight turbine diffuser around the best efficiency point.
Physics of Fluids,
Vol. 35,
Issue. 5,
Lahooti, Mohsen
Bao, Yan
Scott, David
Palacios, Rafael
and
Sherwin, Spencer J.
2023.
LES/DNS fluid-structure interaction simulation of non-linear slender structures in Nektar++ framework.
Computer Physics Communications,
Vol. 282,
Issue. ,
p.
108528.
Buron, Jean-David
and
Houde, Sébastien
2023.
Exploration of transient flow perturbations in a bulb turbine diffuser using proper orthogonal decomposition.
Physics of Fluids,
Vol. 35,
Issue. 8,
 (based on bulk velocity and inflow-duct height), where mean flow characteristics were first studied experimentally by Cherry, Elkins and Eaton (Intl J. Heat Fluid Flow, vol. 29, 2008, pp. 803–811) and later numerically by Ohlsson et al. (J. Fluid Mech., vol. 650, 2010, pp. 307–318). Coherent structures are educed by proper orthogonal decomposition (POD) of the flow, which together with time probes located in the flow domain are used to extract frequency information. The present study shows that the flow contains multiple phenomena, well separated in frequency space. Dominant large-scale frequencies in a narrow band
(based on bulk velocity and inflow-duct height), where mean flow characteristics were first studied experimentally by Cherry, Elkins and Eaton (Intl J. Heat Fluid Flow, vol. 29, 2008, pp. 803–811) and later numerically by Ohlsson et al. (J. Fluid Mech., vol. 650, 2010, pp. 307–318). Coherent structures are educed by proper orthogonal decomposition (POD) of the flow, which together with time probes located in the flow domain are used to extract frequency information. The present study shows that the flow contains multiple phenomena, well separated in frequency space. Dominant large-scale frequencies in a narrow band 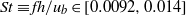 (where
(where 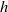 is the inflow-duct height and
is the inflow-duct height and 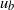 is the bulk velocity), yielding time periods
is the bulk velocity), yielding time periods 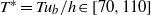 , are deduced from the time signal probes in the upper separated part of the diffuser. The associated structures identified by the POD are large streaks arising from a sinusoidal oscillating motion in the diffuser. Their individual contributions to the total kinetic energy, dominated by the mean flow, are, however, small. The reason for the oscillating movement in this low-frequency range is concluded to be the confinement of the flow in this particular geometric set-up in combination with the high Reynolds number and the large separated zone on the top diffuser wall. Based on this analysis, it is shown that the bulk of the streamwise root mean square (r.m.s.) value arises due to large-scale motion, which in turn can explain the appearance of two or more peaks in the streamwise r.m.s. value. The weak secondary flow present in the inflow duct is shown to survive into the diffuser, where it experiences an imbalance with respect to the upper expanding corners, thereby giving rise to the asymmetry of the mean separated region in the diffuser.
, are deduced from the time signal probes in the upper separated part of the diffuser. The associated structures identified by the POD are large streaks arising from a sinusoidal oscillating motion in the diffuser. Their individual contributions to the total kinetic energy, dominated by the mean flow, are, however, small. The reason for the oscillating movement in this low-frequency range is concluded to be the confinement of the flow in this particular geometric set-up in combination with the high Reynolds number and the large separated zone on the top diffuser wall. Based on this analysis, it is shown that the bulk of the streamwise root mean square (r.m.s.) value arises due to large-scale motion, which in turn can explain the appearance of two or more peaks in the streamwise r.m.s. value. The weak secondary flow present in the inflow duct is shown to survive into the diffuser, where it experiences an imbalance with respect to the upper expanding corners, thereby giving rise to the asymmetry of the mean separated region in the diffuser.