Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Wenwei
and
Wu, Chuan-Yu
2021.
Lateral migration of a neutrally buoyant particle in Couette flow with thermal convection.
International Journal of Multiphase Flow,
Vol. 138,
Issue. ,
p.
103612.
Shao, Yachan
Ruan, Xuan
and
Li, Shuiqing
2021.
Mechanism for clogging of microchannels by small particles with liquid cohesion.
AIChE Journal,
Vol. 67,
Issue. 7,
Pu, Hang
Dong, Ming
Shang, Yan
Zhang, Zeping
and
Wang, Shuang
2021.
Numerical Investigation of Micro-Particle Agglomeration Phenomenon Under the Influence of Cylindrical Vortex Wake.
SSRN Electronic Journal ,
Zhao, K.
Pomes, F.
Vowinckel, B.
Hsu, T.-J.
Bai, B.
and
Meiburg, E.
2021.
Flocculation of suspended cohesive particles in homogeneous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 921,
Issue. ,
Jiang, Meng
Liu, Xiaowei
Han, Jinke
Zhou, Zijian
and
Xu, Minghou
2021.
Measuring particle size and concentration of non-spherical particles by combined light extinction and scattering method.
Measurement,
Vol. 184,
Issue. ,
p.
109911.
Ruan, Xuan
Chen, Sheng
and
Li, Shuiqing
2021.
Effect of long-range Coulomb repulsion on adhesive particle agglomeration in homogeneous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Liu, Wenwei
and
Wu, Chuan-Yu
2021.
Inertial migration of a neutrally buoyant circular particle in a planar Poiseuille flow with thermal fluids.
Physics of Fluids,
Vol. 33,
Issue. 6,
Xu, Jingying
Lyu, Yue
Zhuo, Jiankun
Xu, Yishu
Zhou, Zijian
and
Yao, Qiang
2021.
Formation and emission characteristics of VOCs from a coal-fired power plant.
Chinese Journal of Chemical Engineering,
Vol. 35,
Issue. ,
p.
256.
Yang, Yuandong
Yao, Shun
Liu, Wenqiang
Hu, Yingchao
Li, Qiuwan
Li, Zexin
Zhou, Shimeng
and
Zhou, Zijian
2021.
Novel synthesis of tailored Li4SiO4-based microspheres for ultrafast CO2 adsorption.
Fuel Processing Technology,
Vol. 213,
Issue. ,
p.
106675.
Liu, Wenwei
and
Wu, Chuan-Yu
2021.
Inertial migration of a non-neutrally buoyant particle in a linear shear flow with thermal convection.
Physical Review Fluids,
Vol. 6,
Issue. 6,
Han, Jingkun
Yu, Dunxi
Wu, Jianqun
Yu, Xin
Liu, Fangqi
Wang, Zihao
and
Xu, Minghou
2021.
Co-firing raw and torrefied rice husk with a high-Na/Ca/Cl coal: Impacts on fine particulates emission and elemental partitioning.
Fuel,
Vol. 292,
Issue. ,
p.
120327.
Yao, Yuan
and
Capecelatro, Jesse
2021.
Deagglomeration of cohesive particles by turbulence.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Qian, Yunzhou
Usher, Shane P.
Scales, Peter J.
Stickland, Anthony D.
and
Alexiadis, Alessio
2022.
Agglomeration Regimes of Particles under a Linear Laminar Flow: A Numerical Study.
Mathematics,
Vol. 10,
Issue. 11,
p.
1931.
Qian, Xiaoyu
Ruan, Xuan
and
Li, Shuiqing
2022.
Effect of interparticle dipolar interaction on pore clogging during microfiltration.
Physical Review E,
Vol. 105,
Issue. 1,
Chen, Pinzhuo
Chen, Sheng
Wu, Tianyi
Ruan, Xuan
and
Li, Shuiqing
2022.
Deposition velocity of inertial particles driven by wall-normal external force in turbulent channel flow.
Physical Review Fluids,
Vol. 7,
Issue. 10,
Li, Xiaomin
Gong, Xun
Zhang, Chuxuan
Feng, Tianyi
Ouyang, Zhipeng
and
Peng, Yang
2022.
Comparison of PM10 emission from co-combustion of Platanus orientalis leaf and wood in different seasons with coal.
Fuel Processing Technology,
Vol. 234,
Issue. ,
p.
107334.
Ruan, Xuan
and
Li, Shuiqing
2022.
Effect of electrostatic interaction on impact breakage of agglomerates formed by charged dielectric particles.
Physical Review E,
Vol. 106,
Issue. 3,
Chen, Sheng
Chen, Pinzhuo
and
Fu, Jianhong
2022.
Drag and lift forces acting on linear and irregular agglomerates formed by spherical particles.
Physics of Fluids,
Vol. 34,
Issue. 2,
Icardi, Matteo
Pasquale, Nicodemo Di
Crevacore, Eleonora
Marchisio, Daniele
and
Babler, Matthaus U.
2023.
Population Balance Models for Particulate Flows in Porous Media: Breakage and Shear-Induced Events.
Transport in Porous Media,
Vol. 146,
Issue. 1-2,
p.
197.
Gu, Hailin
Feng, Jie
Yang, Jianzhi
Luo, Kun
Liu, Maosheng
Yu, Mingzhou
Xu, Jiangrong
and
Zhang, Guangxue
2023.
A new drag model of chain-like agglomerates in Stokes region.
Chemical Engineering Science,
Vol. 277,
Issue. ,
p.
118859.
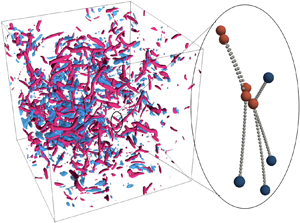
 $Ad_n$ is constructed to quantify the possibility of occurrence of sticking, rebound and breakage events. The collision-induced breakage rate is then formulated based on the Smoluchowski equation and a breakage fraction. The breakage fraction, defined as the fraction of collisions that result in breakage, is then analytically estimated by a convolution of the probability distribution of collision velocity and a universal transfer function. It is shown that the breakage rate decreases exponentially as the adhesion parameter
$Ad_n$ is constructed to quantify the possibility of occurrence of sticking, rebound and breakage events. The collision-induced breakage rate is then formulated based on the Smoluchowski equation and a breakage fraction. The breakage fraction, defined as the fraction of collisions that result in breakage, is then analytically estimated by a convolution of the probability distribution of collision velocity and a universal transfer function. It is shown that the breakage rate decreases exponentially as the adhesion parameter  $Ad_n$ increases for doublets and scales as linear functions of the agglomerate size, with the slope controlled by
$Ad_n$ increases for doublets and scales as linear functions of the agglomerate size, with the slope controlled by  $Ad_n$. These results allow one to estimate the breakage rate for early stage agglomerates of arbitrary size. Moreover, the role of the flow structure on the collision-induced breakage is also examined. Violent collisions and breakages are more likely caused by particles ejected rapidly from strong vortices and happen in straining sheets. Our results extend the findings of shear-induced fragmentation, forming a more complete picture of breakage of agglomerates in turbulent flows.
$Ad_n$. These results allow one to estimate the breakage rate for early stage agglomerates of arbitrary size. Moreover, the role of the flow structure on the collision-induced breakage is also examined. Violent collisions and breakages are more likely caused by particles ejected rapidly from strong vortices and happen in straining sheets. Our results extend the findings of shear-induced fragmentation, forming a more complete picture of breakage of agglomerates in turbulent flows.