Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T01:25:01.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Competing flow and collision effects in a monodispersed liquid–solid fluidized bed at a moderate Archimedes number

Published online by Cambridge University Press:  28 September 2021

Yinuo Yao Open the ORCID record for Yinuo Yao [Opens in a new window] ,
Craig S. Criddle Open the ORCID record for Craig S. Criddle [Opens in a new window]  and
Oliver B. Fringer Open the ORCID record for Oliver B. Fringer [Opens in a new window]
Yinuo Yao*
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA Codiga Resource Recovery Center at Stanford, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Craig S. Criddle
Affiliation:
Codiga Resource Recovery Center at Stanford, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Oliver B. Fringer
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: yaoyinuo@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

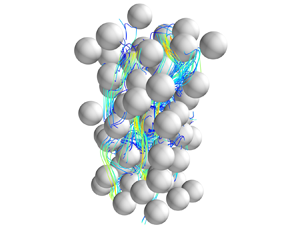
We study the effects of fluid–particle and particle–particle interactions in a three-dimensional monodispersed reactor with unstable fluidization. Simulations were conducted using the immersed boundary method for particle Reynolds numbers of 20–70 with an Archimedes number of 23 600. Two different flow regimes were identified as a function of the particle Reynolds number. For low particle Reynolds numbers ($20 < Re_p < 40$), the porosity is relatively low and the particle dynamics are dominated by interparticle collisions that produce anisotropic particle velocity fluctuations. The relative importance of hydrodynamic effects increases with increasing particle Reynolds number, leading to a minimized anisotropy in the particle velocity fluctuations at an intermediate particle Reynolds number. For high particle Reynolds numbers ($Re_p > 40$), the particle dynamics are dominated by hydrodynamic effects, leading to decreasing and more anisotropic particle velocity fluctuations. A sharp increase in the anisotropy occurs when the particle Reynolds number increases from 40 to 50, corresponding to a transition from a regime in which collision and hydrodynamic effects are equally important (regime 1) to a hydrodynamic-dominated regime (regime 2). The results imply an optimum particle Reynolds number of roughly 40 for the investigated Archimedes number of 23 600 at which mixing in the reactor is expected to peak, which is consistent with reactor studies showing peak performance at a similar particle Reynolds number and with a similar Archimedes number. Results also show that maximum effective collisions are attained at intermediate particle Reynolds number. Future work is required to relate optimum particle Reynolds number to Archimedes number.

JFM classification

Multiphase and Particle-laden Flows: Fluidized beds Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A28
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akiki, G., Jackson, T.L. & Balachandar, S. 2016 Force variation within arrays of monodisperse spherical particles. Phys. Rev. Fluids 1 (4), 044202.CrossRefGoogle Scholar
Akiki, G., Jackson, T.L. & Balachandar, S. 2017 a Pairwise interaction extended point-particle model for a random array of monodisperse spheres. J. Fluid Mech. 813, 882–928.CrossRefGoogle Scholar
Akiki, G., Moore, W.C. & Balachandar, S. 2017 b Pairwise-interaction extended point-particle model for particle-laden flows. J. Comput. Phys. 351, 329–357.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
Biegert, E.K. 2018 Eroding uncertainty: towards understanding flows interacting with mobile sediment beds using grain-resolving simulations. PhD thesis, UC Santa Barbara.Google Scholar
Biegert, E., Vowinckel, B. & Meiburg, E. 2017 A collision model for grain-resolving simulations of flows over dense, mobile, polydisperse granular sediment beds. J. Comput. Phys. 340, 105–127.CrossRefGoogle Scholar
Chang, H.T., Rittmann, B.E., Amar, D., Heim, R., Ehlinger, O. & Lesty, Y. 1991 Biofilm detachment mechanisms in a liquid-fluidized bed. Biotechnol. Bioengng 38 (5), 499–506.CrossRefGoogle Scholar
Chow, E., Cleary, A.J. & Falgout, R.D. 1998 Design of the HYPRE preconditioner library. In SIAM Workshop on Object Oriented Methods for Inter-operable Scientific and Engineering Computing. SIAM.Google Scholar
Costa, P., Boersma, B.J., Westerweel, J. & Breugem, W.-P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.CrossRefGoogle ScholarPubMed
Derksen, J.J. & Sundaresan, S. 2007 Direct numerical simulations of dense suspensions: wave instabilities in liquid-fluidized beds. J. Fluid Mech. 587, 303–336.CrossRefGoogle Scholar
Di Felice, R. 1995 Hydrodynamics of liquid fluidisation. Chem. Engng Sci. 50 (8), 1213–1245.CrossRefGoogle Scholar
Di Felice, R. 1999 The sedimentation velocity of dilute suspensions of nearly monosized spheres. Intl J. Multiphase Flow 25 (4), 559–574.CrossRefGoogle Scholar
Di Felice, R. & Parodi, E. 1996 Wall effects on the sedimentation velocity of suspensions in viscous flow. AIChE J. 42 (4), 927–931.CrossRefGoogle Scholar
Dieterich, J.H. 1972 Time-dependent friction in rocks. J. Geophys. Res. 77 (20), 3690–3697.CrossRefGoogle Scholar
Duru, P., Nicolas, M., Hinch, J. & Guazzelli, É. 2002 Constitutive laws in liquid-fluidized beds. J. Fluid Mech. 452, 371–404.CrossRefGoogle Scholar
Esteghamatian, A., Hammouti, A., Lance, M. & Wachs, A. 2017 Particle resolved simulations of liquid/solid and gas/solid fluidized beds. Phys. Fluids 29 (3), 033302.CrossRefGoogle Scholar
Falgout, R.D. 2006 An introduction to algebraic multigrid. Comput. Sci. Engng 8 (6), 24–33.CrossRefGoogle Scholar
Finn, J. & Apte, S.V. 2013 Relative performance of body fitted and fictitious domain simulations of flow through fixed packed beds of spheres. Intl J. Multiphase Flow 56, 54–71.CrossRefGoogle Scholar
Foerster, S.F., Louge, M.Y., Chang, H. & Allia, K. 1994 Measurements of the collision properties of small spheres. Phys. Fluids 6 (3), 1108–1115.CrossRefGoogle Scholar
Garside, J. & Al-Dibouni, M.R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid–liquid systems. Ind. Engng Chem. Process Des. Dev. 16 (2), 206–214.CrossRefGoogle Scholar
Geldart, D. 1973 Types of gas fluidization. Powder Technol. 7 (5), 285–292.CrossRefGoogle Scholar
Gjaltema, A., Vinke, J.L., van Loosdrecht, M.C. & Heijnen, J.J. 1997 Abrasion of suspended biofilm pellets in airlift reactors: importance of shape, structure, and particle concentrations. Biotechnol. Bioengng 53 (1), 88–99.3.0.CO;2-5>CrossRefGoogle ScholarPubMed
Ham, J.M. & Homsy, G.M. 1988 Hindered settling and hydrodynamic dispersion in quiescent sedimenting suspensions. Intl J. Multiphase Flow 14 (5), 533–546.CrossRefGoogle Scholar
Hamid, A., Molina, J.J. & Yamamoto, R. 2014 Direct numerical simulations of sedimenting spherical particles at non-zero Reynolds number. RSC Adv. 4 (96), 53681–53693.CrossRefGoogle Scholar
Jaafari, J., Mesdaghinia, A., Nabizadeh, R., Hoseini, M., Kamani, H. & Mahvi, A.H. 2014 Influence of upflow velocity on performance and biofilm characteristics of Anaerobic Fluidized Bed Reactor (AFBR) in treating high-strength wastewater. J. Environ. Health Sci. Engng 12 (1), 139.CrossRefGoogle ScholarPubMed
Joseph, G.G. & Hunt, M.L. 2004 Oblique particle–wall collisions in a liquid. J. Fluid Mech. 510, 71–93.CrossRefGoogle Scholar
Joseph, G.G., Zenit, R., Hunt, M.L. & Rosenwinkel, A.M. 2001 Particle–wall collisions in a viscous fluid. J. Fluid Mech. 433, 329–346.CrossRefGoogle Scholar
Kempe, T. & Fröhlich, J. 2012 a An improved immersed boundary method with direct forcing for the simulation of particle laden flows. J. Comput. Phys. 231 (9), 3663–3684.CrossRefGoogle Scholar
Kempe, T. & Fröhlich, J. 2012 b Collision modelling for the interface-resolved simulation of spherical particles in viscous fluids. J. Fluid Mech. 709, 445–489.CrossRefGoogle Scholar
Kidanemariam, A.G., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 Direct numerical simulation of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15 (2), 025031.CrossRefGoogle Scholar
Kriebitzsch, S.H.L., van der Hoef, M.A. & Kuipers, J.A.M. 2013 Fully resolved simulation of a gas-fluidized bed: A critical test of DEM models. Chem. Engng Sci. 91, 1–4.CrossRefGoogle Scholar
Lee, H. & Balachandar, S. 2010 Drag and lift forces on a spherical particle moving on a wall in a shear flow at finite Re. J. Fluid Mech. 657, 89–125.CrossRefGoogle Scholar
Lee, H., Ha, M.Y. & Balachandar, S. 2011 Rolling/sliding of a particle on a flat wall in a linear shear flow at finite Re. Intl J. Multiphase Flow 37 (2), 108–124.CrossRefGoogle Scholar
Legendre, D., Zenit, R., Daniel, C. & Guiraud, P. 2006 A note on the modelling of the bouncing of spherical drops or solid spheres on a wall in viscous fluid. Chem. Engng Sci. 61 (11), 3543–3549.CrossRefGoogle Scholar
Lu, J., Peters, E.A.J.F. & Kuipers, J.A.M. 2020 Direct numerical simulation of mass transfer in bidisperse arrays of spheres. AIChE J. 66 (1), 1–17.CrossRefGoogle Scholar
Nicolai, H., Herzhaft, B., Hinch, E.J., Oger, L. & Guazzelli, E. 1995 Particle velocity fluctuations and hydrodynamic self-diffusion of sedimenting non-Brownian spheres. Phys. Fluids 7 (1), 12–23.CrossRefGoogle Scholar
Nicolella, C., Chiarle, S., Di Felice, R. & Rovatti, M. 1997 Mechanisms of biofilm detachment in fluidized bed reactors. Water Sci. Technol. 36 (1), 229–235.CrossRefGoogle Scholar
Nicolella, C., Di Felice, R. & Rovatti, M. 1996 An experimental model of biofilm detachment in liquid fluidized bed biological reactors. Biotechnol. Bioengng 51 (6), 713–719.3.0.CO;2-E>CrossRefGoogle ScholarPubMed
Ozel, A., Brändle de Motta, J.C., Abbas, M., Fede, P., Masbernat, O., Vincent, S., Estivalezes, J.-L. & Simonin, O. 2017 Particle resolved direct numerical simulation of a liquid–solid fluidized bed: comparison with experimental data. Intl J. Multiphase Flow 89, 228–240.CrossRefGoogle Scholar
Pan, H., Chen, X.-Z., Liang, X.-F., Zhu, L.-T. & Luo, Z.-H. 2016 CFD simulations of gas–liquid–solid flow in fluidized bed reactors – a review. Powder Technol. 299, 235–258.CrossRefGoogle Scholar
Peskin, C.S. 1977 Numerical analysis of blood flow in the heart. J. Comput. Phys. 25 (3), 220–252.CrossRefGoogle Scholar
Rai, M. & Moin, P. 1991 Direct simulations of turbulent flow using finite-difference schemes. J. Comput. Phys. 96 (1), 15–53.Google Scholar
Richardson, J.F. & Zaki, W.N. 1954 Sedimentation and fluidisation: part I. Trans. Inst. Chem. Engng 32, 35–53.Google Scholar
Rittmann, B.E. & McCarty, P.L. 2018 Environmental Biotechnology: Principles and Applications. McGraw-Hill Education.Google Scholar
Roma, A.M., Peskin, C.S. & Berger, M.J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.CrossRefGoogle Scholar
Shajahan, T. & Breugem, W.-P. 2020 Influence of concentration on sedimentation of a dense suspension in a viscous fluid. Flow Turbul. Combust. 105 (2), 537–554.CrossRefGoogle Scholar
Shin, C., Bae, J. & McCarty, P.L. 2012 Lower operational limits to volatile fatty acid degradation with dilute wastewaters in an anaerobic fluidized bed reactor. Bioresour. Technol. 109, 13–20.CrossRefGoogle Scholar
Shin, C., Lee, E., McCarty, P.L. & Bae, J. 2011 Effects of influent DO/COD ratio on the performance of an anaerobic fluidized bed reactor fed low-strength synthetic wastewater. Bioresour. Technol. 102 (21), 9860–9865.CrossRefGoogle ScholarPubMed
Shin, C., McCarty, P.L., Kim, J. & Bae, J. 2014 Pilot-scale temperate-climate treatment of domestic wastewater with a staged anaerobic fluidized membrane bioreactor (SAF-MBR). Bioresour. Technol. 159, 95–103.CrossRefGoogle Scholar
Sundaresan, S. 2003 Instabilities in fluidized beds. Annu. Rev. Fluid Mech. 35 (1), 63–88.CrossRefGoogle Scholar
Tang, Y., Peters, E.A.J.F., Kuipers, J.A.M., Kriebitzsch, S.H.L. & van der Hoef, M.A. 2015 A new drag correlation from fully resolved simulations of flow past monodisperse static arrays of spheres. AIChE J. 61 (2), 688–698.CrossRefGoogle Scholar
Tenneti, S., Garg, R. & Subramaniam, S. 2011 Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Intl J. Multiphase Flow 37 (9), 1072–1092.CrossRefGoogle Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.CrossRefGoogle Scholar
Verma, V., Padding, J.T., Deen, N.G. & Hans Kuipers, J.A.M. 2015 Effect of bed size on hydrodynamics in 3-D gas-solid fluidized beds. AIChE J. 61 (5), 1492–1506.CrossRefGoogle Scholar
Verma, V., Padding, J.T., Deen, N.G. & Kuipers, J.A.M.H. 2014 Numerical investigation on the effect of pressure on fluidization in a 3D fluidized bed. Ind. Engng Chem. Res. 53 (44), 17487–17498.CrossRefGoogle Scholar
Wallis, G.B. 2020 One-Dimensional Two-Phase Flow. Courier Dover Publications.Google Scholar
Wang, Z., Fan, J. & Luo, K. 2008 Combined multi-direct forcing and immersed boundary method for simulating flows with moving particles. Intl J. Multiphase Flow 34 (3), 283–302.CrossRefGoogle Scholar
Willen, D.P. & Prosperetti, A. 2019 Resolved simulations of sedimenting suspensions of spheres. Phys. Rev. Fluids 4 (1), 014304.CrossRefGoogle Scholar
Willen, D.P., Sierakowski, A.J., Zhou, G. & Prosperetti, A. 2017 Continuity waves in resolved-particle simulations of fluidized beds. Phys. Rev. Fluids 2 (11), 114305.CrossRefGoogle Scholar
Yang, M., Yu, D., Liu, M., Zheng, L., Zheng, X., Wei, Y., Wang, F. & Fan, Y. 2017 Optimization of MBR hydrodynamics for cake layer fouling control through CFD simulation and RSM design. Bioresour. Technol. 227, 102–111.CrossRefGoogle ScholarPubMed
Yao, Y., Criddle, C.S. & Fringer, O.B. 2021 a Comparison of the properties of segregated layers in a bidispersed fluidized bed to those of a monodispersed fluidized bed. Phys. Rev. Fluids 6, 084306.CrossRefGoogle Scholar
Yao, Y., Criddle, C.S. & Fringer, O.B. 2021 b The effects of particle clustering on hindered settling in high-concentration particle suspensions. J. Fluid Mech. 920, A40.CrossRefGoogle Scholar
Yin, X. & Koch, D.L. 2007 Hindered settling velocity and microstructure in suspensions of solid spheres with moderate Reynolds numbers. Phys. Fluids 19 (9), 093302.CrossRefGoogle Scholar
Yin, X. & Koch, D.L. 2008 Lattice-Boltzmann simulation of finite Reynolds number buoyancy-driven bubbly flows in periodic and wall-bounded domains. Phys. Fluids 20 (10), 103304.CrossRefGoogle Scholar
Yu, A. & Xu, B. 2003 Particle-scale modelling of gas-solid flow in fluidisation. J. Chem. Technol. Biotechnol. 78 (2–3), 111–121.CrossRefGoogle Scholar
Zaidi, A.A., Tsuji, T. & Tanaka, T. 2015 Hindered settling velocity & structure formation during particle settling by direct numerical simulation. Procedia Engng 102, 1656–1666.CrossRefGoogle Scholar
Zang, Y., Street, R.L. & Koseff, J.R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114 (1), 18–33.CrossRefGoogle Scholar
Zenit, R. & Hunt, M.L. 2000 Solid fraction fluctuations in solid–liquid flows. Intl J. Multiphase Flow 26 (5), 763–781.CrossRefGoogle Scholar
Zenit, R., Hunt, M.L. & Brennen, C.E. 1997 Collisional particle pressure measurements in solid–liquid flows. J. Fluid Mech. 353, 261–283.CrossRefGoogle Scholar
Zhang, Z. & Prosperetti, A. 2005 A second-order method for three-dimensional particle simulation. J. Comput. Phys. 210 (1), 292–324.CrossRefGoogle Scholar