Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T07:10:16.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Complex solutions of the Dean equations and non-uniqueness at all Reynolds numbers

Published online by Cambridge University Press:  29 March 2017

F. A. T. Boshier  and
A. J. Mestel Open the ORCID record for A. J. Mestel [Opens in a new window]
F. A. T. Boshier
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
A. J. Mestel*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: j.mestel@ic.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Steady incompressible flow down a slowly curving circular pipe is considered, analytically and numerically. Both real and complex solutions are investigated. Using high-order Hermite–Padé approximants, the Dean series solution is analytically continued outside its circle of convergence, where it predicts a complex solution branch for real positive Dean number, 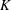$K$. This is confirmed by numerical solution. It is shown that other previously unknown solution branches exist for all 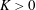$K>0$, which are related to an unforced complex eigensolution. This non-uniqueness is believed to be generic to the Navier–Stokes equations in most geometries. By means of path continuation, numerical solutions are followed around the complex 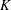$K$-plane. The standard Dean two-vortex solution is shown to lie on the same hypersurface as the eigensolution and the four-vortex solutions found in the literature. Elliptic pipes are considered and shown to exhibit similar behaviour to the circular case. There is an imaginary singularity limiting convergence of the Dean series, an unforced solution at 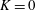$K=0$ and non-uniqueness for 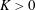$K>0$, culminating in a real bifurcation.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Mathematical Foundations: Mathematical Foundations
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 241 - 259
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boshier, F. A. T. & Mestel, A. J. 2014 Extended series solutions and bifurcations of the Dean equations. J. Fluid Mech. 739, 179–195.Google Scholar
Daskopoulos, P. & Lenhoff, A. M. 1989 Flow in curved ducts: bifurcation structure for stationary ducts. J. Fluid Mech. 203, 125–148.Google Scholar
Dean, W. R. 1928 The stream-line motion of fluid in a curved pipe. Phil. Mag. 5, 673–695.Google Scholar
Drazin, P. G. & Tourigny, Y. 1996 Numerical study of bifurcations by analytic continuation of a function defined by a power series. SIAM J. Appl. Maths 56, 1–18.Google Scholar
Free Software Foundation2013 The GNU MP Bignum Library, https://gmplib.org.Google Scholar
Henderson, M. E. & Keller, H. B. 1990 Complex bifurcation from real paths. SIAM J. Appl. Maths 50 (2), 460–482.CrossRefGoogle Scholar
Machane, W. 2010 Bifurcation and stability analysis for laminar flow in curved ducts. Intl J. Numer. Meth. Fluids 64, 355–375.Google Scholar
McConalogue, D. J. & Srivastava, R. S. 1968 Motion of a fluid in a curved tube. Proc. R. Soc. Lond. A 307, 37–53.Google Scholar
Mestel, A. J. & Zabielski, L. 2012 Laminar instability of pressure-driven dynamos in multiple helical pipes. Geophys. Astrophys. Fluid Dyn. 106, 493–507.Google Scholar
Siggers, J. H. & Waters, S. L. 2008 Unsteady flows in pipes with finite curvature. J. Fluid Mech. 600, 133–165.CrossRefGoogle Scholar
Tettamanti, F. A.2012 Extended Stokes series for Dean flow in weakly curved pipes. PhD thesis, Imperial College London.Google Scholar
Van Dyke, M. 1974 Analysis and improvement of perturbation series. Q. J. Mech. Appl. Maths 27, 423–450.Google Scholar
Vaz, R. H., Boshier, F. A. T. & Mestel, A. J.2017 Flow in a curved channel driven by a linearly-varying horizontal temperature gradient (in preparation).Google Scholar