Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T21:03:14.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Density difference-driven segregation in a dense granular flow

Published online by Cambridge University Press:  01 February 2013

Anurag Tripathi  and
D. V. Khakhar
Anurag Tripathi
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
D. V. Khakhar*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
*
†Email address for correspondence: khakhar@iitb.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the segregation of spheres of equal size and different density flowing over an inclined plane, theoretically and computationally by means of distinct element method (DEM) simulations. In the first part of the work, we study the settling of a single higher-density particle in the flow of otherwise identical particles. We show that the motion of the high-density tracer particle can be understood in terms of the buoyancy and drag forces acting on it. 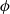The buoyancy force is given by Archimedes principle, with an effective volume associated with the particle, which depends upon the local packing fraction, $\phi $. The buoyancy arises primarily from normal forces acting on the particle, and tangential forces have a negligible contribution. The drag force on a sphere of diameter 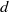$d$ sinking with a velocity $v$ in a granular medium of apparent viscosity 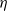$\eta $ is given by a modified Stokes law, 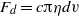${F}_{d} = c\pi \eta dv$. The coefficient ($c$) is found to decrease with packing fraction. In the second part of the work, we consider the case of binary granular mixtures of particles of the same size but differing in density. A continuum model for segregation is presented, based on the single-particle results. The number fraction profile for the heavy particles at equilibrium is obtained in terms of the effective temperature, defined by a fluctuation–dissipation relation. The model predicts the equilibrium number fraction profiles at different inclination angles and for different mass ratios of the particles, which match the DEM results very well. Finally, a complete model for the theoretical prediction of the flow and number fraction profiles for a mixture of particles of different density is presented, which combines the segregation model with a model for the rheology of mixtures. The model predictions agree quite well with the simulation results.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 643 - 669
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albert, R., Pfeifer, M. A., Barabási, A.-L. & Schiffer, P. 1999 Slow drag in a granular medium. Phys. Rev. Lett. 82 (1), 205–208.CrossRefGoogle Scholar
Barrat, J. L. & Berthier, L. 2000 Fluctuation–dissipation relation in a sheared fluid. Phys. Rev. E 63 (1), 012503.CrossRefGoogle Scholar
Berthier, L. & Barrat, J. L. 2002 Shearing a glassy material: numerical tests of nonequilibrium mode-coupling approaches and experimental proposals. Phys. Rev. Lett. 89, 095702.Google Scholar
Berthier, L., Barrat, J. L. & Kurchan, J. 2000 A two-time scale, two-temperature scenario for nonlinear rheology. Phys. Rev. E 61, 5464.CrossRefGoogle ScholarPubMed
Brito, R., Enriquez, H., Godoy, S. & Soto, R. 2008 Segregation induced by inelasticity in a vibrofluidized granular mixture. Phys. Rev. E 77 (6), 061301.CrossRefGoogle Scholar
Brito, R. & Soto, R. 2009 Competition of brazil nut effect, buoyancy, and inelasticity induced segregation in a granular mixture. Eur. Phys. J. Special Topics 179, 207–219.Google Scholar
Caballero-Robledo, G. A. & Clement, E. 2009 Rheology of a sonofluidized granular packing. Eur. Phys. J. E 30, 395–401.Google Scholar
Candelier, R. & Dauchot, O. 2009 Creep motion of an intruder within a granular glass close to jamming. Phys. Rev. Lett. 103 (12), 128001.CrossRefGoogle ScholarPubMed
Candelier, R. & Dauchot, O. 2010 Journey of an intruder through the fluidization and jamming transitions of a dense granular media. Phys. Rev. E 81 (1), 011304.CrossRefGoogle ScholarPubMed
Chehata, D., Zenit, R. & Wassgren, C. R. 2003 Dense granular flow around an immersed cylinder. Phys. Fluids 15, 1622.Google Scholar
Chung, F., Liaw, S.-S. & Ju, C.-Y. 2009 Brazil nut effect in a rectangular plate under horizontal vibration. Granul. Matt. 11, 79–86.CrossRefGoogle Scholar
Cisar, S. E., Umbanhowar, P. B. & Ottino, J. M. 2006 Radial granular segregation under chaotic flow in two-dimensional tumblers. Phys. Rev. E 74 (5), 051305.Google Scholar
Costantino, D. J., Bartell, J., Scheidler, K. & Schiffer, P. 2011 Low-velocity granular drag in reduced gravity. Phys. Rev. E 83 (1), 011305.Google Scholar
Dolgunin, V. N., Kudy, A. N. & Ukolov, A. A. 1998 Development of the model of segregation of particles undergoing granular flow down an inclined plane. Powder Technol. 96, 211–218.Google Scholar
Dolgunin, V. N. & Ukolov, A. A. 1995 Segregation modelling of particle rapid gravity flow. Powder Technol. 83, 95–103.CrossRefGoogle Scholar
Drahun, J. A. & Bridgwater, J. 1983 Mechanisms of free surface segregation. Powder Technol. 36, 39–53.Google Scholar
Dufresne, E. R., Squires, T. M., Brenner, M. P. & Grier, D. G. 2000 Hydrodynamic coupling of two Brownian spheres to a planar surface. Phys. Rev. Lett. 85 (15), 3317–3320.Google Scholar
Duran, J. 2000 Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials. Springer.Google Scholar
Felix, G. & Thomas, N. 2004 Evidence of two effects in the size segregation process in dry granular media. Phys. Rev. E 70, 051307.Google Scholar
Geng, J. & Behringer, R. P. 2005 Slow drag in two-dimensional granular media. Phys. Rev. E 71 (1), 011302.CrossRefGoogle ScholarPubMed
Godoy, S., Risso, D., Soto, R. & Cordero, P. 2008 Rise of a brazil nut: a transition line. Phys. Rev. E 78 (3), 031301.Google Scholar
Gray, J. M. N. T. & Chugunov, V. A. 2006 Particle-size segregation and diffusive remixing in shallow granular avalanches. J. Fluid Mech. 569, 365–398.CrossRefGoogle Scholar
Gray, J. M. N. T. & Thornton, A. R. 2005 A theory for particle size segregation in shallow granular free-surface flows. Proc. R. Soc. A 461, 1447–1473.Google Scholar
Hajra, S. K. & Khakhar, D. V. 2005 Radial mixing of granular materials in a rotating cylinder: experimental determination of particle self-diffusivity. Phys. Fluids 17, 013101.Google Scholar
Hajra, S. K. & Khakhar, D. V. 2011 Radial segregation of ternary granular mixtures in rotating cylinders. Granul. Matt. 13, 475–486.CrossRefGoogle Scholar
Hill, K. M., Khakhar, D. V., Gilchrist, J. F., McCarthy, J. J. & Ottino, J. M. 1999 Segregation-driven organization in chaotic granular flows. Proc. Natl Acad. Sci. USA 96 (21), 11701–11706.Google Scholar
Hirshfeld, D. & Rapaport, D. C. 1997 Molecular dynamics studies of grain segregation in sheared flow. Phys. Rev. E 56 (2), 2012–2018.Google Scholar
Hsiau, S. S. & Chen, W. C. 2002 Density effect of binary mixtures on the segregation process in a vertical shaker. Adv. Powder Technol. 13 (3), 301–315.CrossRefGoogle Scholar
Jain, N., Ottino, J. M. & Lueptow, R. M. 2005 Regimes of segregation and mixing in combined size and density granular systems: an experimental study. Granul. Matt. 7, 69–81.CrossRefGoogle Scholar
Jenkins, J. T. & Mancini, F. 1989 Kinetic theory for binary mixtures of smooth, nearly elastic, spheres. Phys. Fluids A 1, 2050–2057.CrossRefGoogle Scholar
Johnson, C. G., Kokelaar, B. P., Iverson, R. M., Logan, M., LaHusen, R. G. & Gray, J. M. N. T. 2012 Grain-size segregation and levee formation in geophysical mass flows. J. Geophys. Res. Earth Surf. 117, F01032.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A new constitutive law for dense granular flows. Nature 441, 727–730.Google Scholar
Khakhar, D. V., McCarthy, J. J. & Ottino, J. M. 1997 Radial segregation of granular materials in a rotating cylinder. Phys. Fluids 9 (12), 3600–3614.Google Scholar
Khakhar, D. V., McCarthy, J. J. & Ottino, J. M. 1999 Mixing and segregation of granular materials in chute flows. Chaos 9, 594–610.Google Scholar
Khakhar, D. V., Orpe, A. V. & Hajra, S. K. 2003 Segregation of granular materials in rotating cylinders. Physica A 318 (1–2), 129–136.Google Scholar
Kurchan, J. 2000 Emergence of macroscopic temperatures in systems that are not thermodynamical microscopically: towards a thermodynamical description of slow granular rheology. J. Phys.: Condens. Matter 12, 6611.Google Scholar
Lim, E. W. C. 2010 Density segregation in vibrated granular beds with bumpy surfaces. AIChE J. 56, 2588–2597.Google Scholar
Lin, B., Yu, J. & Rice, S. A. 2000 Direct measurements of constrained Brownian motion of an isolated sphere between two walls. Phys. Rev. E 62 (3), 3909–3919.Google Scholar
Linares-Guerrero, E., Goujon, C. & Zenit, R. 2007 Increased mobility of bidisperse granular avalanches. J. Fluid Mech. 593, 475–504.CrossRefGoogle Scholar
Makse, H. A. & Kurchan, J. 2002 Testing the thermodynamic approach to granular matter with a numerical model of a decisive experiment. Nature 415, 614.Google Scholar
Marks, B., Rognon, P. & Einav, I. 2012 Grainsize dynamics of polydisperse granular segregation down inclined planes. J. Fluid Mech. 690, 499–511.Google Scholar
Mehta, A. & Edwards, S. F. 1989 Statistical mechanics of powder mixtures. Physica A 157, 1091.Google Scholar
Ottino, J. M. & Khakhar, D. V. 2000 Mixing and segregation of granular materials. Annu. Rev. Fluid Mech. 32, 55–91.Google Scholar
Pereira, G., Sinnott, M., Cleary, P., Liffman, K., Metcalfe, G. & Štalo, I. 2011 Insights from simulations into mechanisms for density segregation of granular mixtures in rotating cylinders. Granul. Matt. 13, 53–74.CrossRefGoogle Scholar
Phillips, J. C., Hogg, A. J., Kerswell, R. R. & Thomas, N. H. 2006 Enhanced mobility of granular mixtures of fine and coarse particles. Earth Planet. Sci. Lett. 246, 466–480.Google Scholar
Pica Ciamarra, M., Lara, A. H., Lee, A. T., Goldman, D. I., Vishik, I. & Swinney, H. L. 2004 Dynamics of drag and force distributions for projectile impact in a granular medium. Phys. Rev. Lett. 92 (19), 194301.Google Scholar
Pollard, B. L. & Henein, H. 1989 Kinetics of radial segregation of different sized irregular particles in rotary cylinders. Can. Metall. Q. 28 (1), 29–40.Google Scholar
Rapaport, D. C. 2002 Simulational studies of axial granular segregation in a rotating cylinder. Phys. Rev. E 65, 061306.CrossRefGoogle Scholar
Ristow, G. H. 1994 Particle mass segregation in a two-dimensional rotating drum. Europhys. Lett. 28, 97–101.Google Scholar
Sanfratello, L. & Fukushima, E. 2008 Experimental studies of density segregation in the 3D rotating cylinder and the absence of banding. Granul. Matt. 11 (2), 73–78.CrossRefGoogle Scholar
Sarkar, S. & Khakhar, D. V. 2008 Experimental evidence for a description of granular segregation in terms of the effective temperature. Europhys. Lett. 83 (5), 54004.CrossRefGoogle Scholar
Savage, S. B. 1993 Disorder, diffusion and structure formation in granular flow. In Disorder and Granular Media (ed. Hansen, A. & Bideau, D.), pp. 255–285. Elsevier.Google Scholar
Savage, S. B. & Lun, C. K. K. 1988 Particle size segregation in inclined chute flow of dry cohesionless granular solids. J. Fluid Mech. 189, 311–335.Google Scholar
Schröter, M., Ulrich, S., Kreft, J., Swift, J. B. & Swinney, H. L. 2006 Mechanisms in the size segregation of a binary granular mixture. Phys. Rev. E 74 (1), 011307.CrossRefGoogle ScholarPubMed
Shi, Q., Sun, G., Hou, M. & Lu, K. 2007 Density-driven segregation in vertically vibrated binary granular mixtures. Phys. Rev. E 75, 061302.Google Scholar
Silbert, L. E., Ertas, D., Grest, G. S., Hasley, T. C., Levine, D. & Plimpton, S. J. 2001 Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 64, 051302.Google Scholar
Song, C., Wang, P. & Makse, H. A. 2005 Experimental measurement of an effective temperature for jammed granular materials. Proc. Natl Acad. Sci. USA 102, 2299.Google Scholar
Srebro, Y. & Levine, D. 2003 Role of friction in compaction and segregation of granular materials. Phys. Rev. E 68 (6), 061301.Google Scholar
Tai, C. H., Hsiau, S. S. & Kruelle, C. A. 2010 Density segregation in a vertically vibrated granular bed. Powder Technol. 204 (2–3), 255–262.Google Scholar
Takehara, Y., Fujimoto, S. & Okumura, K. 2010 High-velocity drag friction in dense granular media. Europhys. Lett. 92, 44003.Google Scholar
Thomas, N. 2000 Reverse and intermediate segregation of large beads in dry granular media. Phys. Rev. E 62 (1), 961–974.Google Scholar
Tripathi, A. & Khakhar, D. V. 2010 Steady flow of smooth, inelastic particles on a bumpy inclined plane: hard and soft particle simulations. Phys. Rev. E 81 (4), 041307.Google Scholar
Tripathi, A. & Khakhar, D. V. 2011a Numerical simulation of the sedimentation of a sphere in a sheared granular fluid: a granular Stokes experiment. Phys. Rev. Lett. 107, 108001.CrossRefGoogle Scholar
Tripathi, A. & Khakhar, D. V. 2011b Rheology of binary granular mixtures in the dense flow regime. Phys. Fluids 23 (11), 113302.Google Scholar
Ulrich, S., Schröter, M. & Swinney, H. L. 2007 Influence of friction on granular segregation. Phys. Rev. E 76 (4), 042301.Google Scholar
Wassgren, C. R., Cordova, J. A., Zenit, R. & Karion, A. 2003 Dilute granular flow around an immersed cylinder. Phys. Fluids 15, 3318.Google Scholar
Wiederseiner, S., Andreini, N., Epely-Chauvin, G., Moser, G., Monnereau, M., Gray, J. M. N. T. & Ancey, C. 2011 Experimental investigation into segregating granular flows down chutes. Phys. Fluids 23 (1)013301.CrossRefGoogle Scholar
Wieghardt, K. 1975 Experiments in granular flow. Annu. Rev. Fluid Mech. 7, 89–114.Google Scholar
Yang, S. C. 2006 Density effect on mixing and segregation processes in a vibrated granular mixture. Powder Technol. 164, 65–74.Google Scholar
Zhou, F., Advani, S. G. & Wetzel, E. D. 2004 Slow drag in granular materials under high pressure. Phys. Rev. E 69 (6), 061306.Google Scholar
Zhou, F., Advani, S. G. & Wetzel, E. D. 2005 Slow drag in polydisperse granular mixtures under high pressure. Phys. Rev. E 71 (6), 061304.Google Scholar
Zhou, F., Advani, S. G. & Wetzel, E. D. 2007 Simulation of slowly dragging a cylinder through a confined pressurized bed of granular materials using the discrete element method. Phys. Fluids 19, 013301.CrossRefGoogle Scholar
Zik, O., Stavans, J. & Rabin, Y. 1992 Mobility of a sphere in vibrated granular media. Europhys. Lett. 17 (4), 315.CrossRefGoogle Scholar