Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-14T17:55:21.522Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of triboelectric charging in particle-laden turbulent channel flows

Published online by Cambridge University Press:  05 April 2017

Holger Grosshans Open the ORCID record for Holger Grosshans [Opens in a new window]  and
Miltiadis V. Papalexandris
Holger Grosshans*
Affiliation:
Institute of Mechanics, Materials and Civil Engineering, Université catholique de Louvain, 1348 Louvain-la-Neuve, Belgium
Miltiadis V. Papalexandris
Affiliation:
Institute of Mechanics, Materials and Civil Engineering, Université catholique de Louvain, 1348 Louvain-la-Neuve, Belgium
*
†Email address for correspondence: holger-grosshans@gmx.de
Get access Rights & Permissions [Opens in a new window]

Abstract

The electrification of particles embedded in a turbulent flow may cause hazards such as spark discharges but is also exploited in several industrial applications. Nonetheless, due to its complexity and sensitivity to the initial conditions, the process of build-up of particle charge is currently not well understood. In order to gain a deeper understanding of this phenomenon, we performed fully resolved numerical simulations of particle charging. 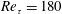More specifically, our study concerned the charging process of particles dispersed in a turbulent channel flow at a friction Reynolds number of $Re_{\unicode[STIX]{x1D70F}}=180$. Emphasis was placed on the analysis of the interplay between the different physical mechanisms underlying particle electrification, such as fluid turbulence, particle dynamics and particle collisions. Further, we investigated the influence of some important physical parameters. According to our simulations the charge build-up depends strongly on the particle Stokes number, $Stk$. In particular, at small Stokes numbers, 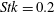$Stk=0.2$, the turbopheretic drift inhibits particle charging. By contrast, at moderate Stokes numbers, 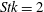$Stk=2$, and low particle number densities, the electric charge builds up but cannot escape the viscous sublayer due to limited particle migration. However, in the case of high particle number densities, the charge is transported away from the wall via inter-particle charge diffusion. A further increase to 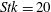$Stk=20$ leads to strong charging and particle-bound charge transport towards the bulk of the channel.

JFM classification

MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 465 - 491
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artana, G., Touchard, G. & Morin, M. F. 1997 Contribution to the analysis of the flow electrification process of powders in pneumatic conveyers. J. Electrostat. 40–41, 277–282.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Baytekin, H. T., Patashisnki, A. Z., Branicki, M., Baytekin, B., Soh, S. & Grzybowski, B. A. 2011 The mosaic of surface charge in contact electrification. Science 33, 308–312.CrossRefGoogle Scholar
Brooke, J. W., Kontomaris, K., Hanratty, T. J. & McLaughlin, J. B. 1992 Turbulent deposition and trapping of aerosols at a wall. Phys. Fluids A 4, 825–834.CrossRefGoogle Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32, 565–568.Google Scholar
Cleaver, J. W. & Yates, B. 1975 A sub layer model for the deposition of particles from a turbulent flow. Chem. Engng Sci. 30, 983–992.CrossRefGoogle Scholar
Crowe, C., Schwarzkopf, J. D., Sommerfeld, M. & Tsuji, Y. 2012 Multiphase Flows with Droplets and Particles, 2nd edn. CRC Press.Google Scholar
De Marchis, M., Milici, B., Sardina, G. & Napoli, E. 2016 Interaction between turbulent structures and particles in roughened channel. Intl J. Multiphase Flow 78, 117–131.CrossRefGoogle Scholar
Diaz, A. F. & Fenzel-Alexander, D. 1993 An ion transfer model for contact charging. Langmuir 9, 1009–1015.CrossRefGoogle Scholar
Eaton, J. K. 2009 Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Intl J. Multiphase Flow 35 (9), 792–800.CrossRefGoogle Scholar
Eckelmann, H. 1974 The structure of the viscous sublayer and the adjacent wall region in a turbulent channel flow. J. Fluid Mech. 65, 439–459.CrossRefGoogle Scholar
Elgobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52, 309–329.CrossRefGoogle Scholar
Fath, W., Blum, C., Glor, M. & Walther, C.-D. 2013 Electrostatic ignition hazards due to pneumatic transport of flammable powders through insulating or dissipative tubes and hoses – new experiments and calculations. J. Electrostat. 71 (3), 377–382.Google Scholar
Grosshans, H., Griesing, M., Hellwig, T., Pauer, W., Moritz, H.-U. & Gutheil, E. 2016a A new model for the drying of mannitol-water droplets in hot air above the boiling temperature. Powder Technol. 297, 259–265.Google Scholar
Grosshans, H., Griesing, M., Mönckedieck, M., Hellwig, T., Walther, B., Gopireddy, S. R., Sedelmayer, R., Pauer, W., Moritz, H.-U., Urbanetz, N. A. et al. 2016b Numerical and experimental study of the drying of bi-component droplets under various drying conditions. Intl J. Heat Mass Transfer 96, 97–109.CrossRefGoogle Scholar
Grosshans, H., Movaghar, A., Cao, L., Oevermann, M., Szász, R.-Z. & Fuchs, L. 2016c Sensitivity of vof simulations of the liquid jet breakup to physical and numerical parameters. Comput. Fluids 136, 312–323.CrossRefGoogle Scholar
Grosshans, H. & Papalexandris, M. V. 2016a Evaluation of the parameters influencing electrostatic charging of powder in a pipe flow. J. Loss Prev. Process Ind. 43, 83–91.Google Scholar
Grosshans, H. & Papalexandris, M. V. 2016b Large eddy simulation of triboelectric charging in pneumatic powder transport. Powder Technol. 301, 1008–1015.CrossRefGoogle Scholar
Grosshans, H. & Papalexandris, M. V. 2016c A model for the non-uniform contact charging of particles. Powder Technol. 305, 518–527.CrossRefGoogle Scholar
Grosshans, H., Szasz, R. Z. & Papalexandris, M. V. 2017 Modeling the electrostatic charging of a helicopter during hovering in dusty atmosphere. Aerosp. Sci. Technol. 64, 31–38.Google Scholar
Grote, K.-H. & Jörg, F. 2007 Dubbel. Springer.Google Scholar
Gullbrand, J., Bai, X. S. & Fuchs, L. 2001 High-order cartesian grid method for calculation of incompressible turbulent flows. Intl J. Numer. Meth. Fluids 36, 687–709.CrossRefGoogle Scholar
Harper, W. R. 1951 The Volta effect as a cause of static electrification. Proc. R. Soc. Lond. A 205, 83–103.Google Scholar
Ireland, P. M. 2012 Dynamic particle-surface tribocharging: the role of shape and contact mode. J. Electrostat. 70, 524–531.Google Scholar
Israel, R. & Rosner, D. E. 1982 Use of a generalized Stokes number to determine the aerodynamic capture efficiency of non-Stokesian particles from a compressible gas flow. Aerosol Sci. Technol. 2, 45–51.Google Scholar
Jang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted eno schemes. J. Comput. Phys. 126, 202–228.Google Scholar
John, W., Reischl, G. & Devor, W. 1980 Charge transfer to metal surfaces from bouncing aerosol particles. J. Aero. Sci. 11 (2), 115–138.Google Scholar
Kamra, A. K. 1972 Physical sciences: visual observation of electric sparks on gypsum dunes. Nature 240, 143–144.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kolniak, P. Z. & Kuczynski, R. 1989 Numerical modeling of powder electrification in pneumatic transport. J. Electrostat. 23, 421–430.Google Scholar
Korevaar, M. W., Padding, J. T., Van der Hoef, M. A. & Kuipers, J. A. M. 2014 Integrated DEM-CFD modeling of the contact charging of pneumatically conveyed powders. Powder Technol. 258, 144–156.Google Scholar
Kreplin, H. & Eckelmann, H. 1979 Behavior of the three fluctuating velocity components in the wall region of a turbulent channel flow. Phys. Fluids 22, 1233–1239.CrossRefGoogle Scholar
Lacks, D. J. 2012 The unpredictability of electrostatic charging. Angew. Chem. Intl Ed. Engl. 51, 6822–6823.Google Scholar
Laurentie, J. C., Traoré, P. & Dascalescu, L. 2013 Discrete element modeling of triboelectric charging of insulating materials in vibrated granular beds. J. Electrostat. 71 (6), 951–957.CrossRefGoogle Scholar
Lim, E. W. C., Yao, J. & Zhao, Y. 2012 Pneumatic transport of granular materials with electrostatic effects. AIChE J. 58 (4), 1040–1059.CrossRefGoogle Scholar
Lowell, J. & Rose-Innes, A. C. 1980 Contact electrification. Adv. Phys. 29, 947–1023.Google Scholar
Marchioli, C., Picciotto, M. & Soldati, A. 2007 Influence of gravity and lift on particle velocity statistics and transfer rates in turbulent vertical channel flow. Intl J. Multiphase Flow 33, 227–251.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 48, 283–315.CrossRefGoogle Scholar
Masuda, H., Komatsu, T. & Iinoya, K. 1976 The static electrification of particles in gas–solids pipe flow. AIChE J. 22, 558–564.Google Scholar
Masui, N. & Murata, Y. 1983 Electrification of polymer particles by impact on a metal plate. Japan. J. Appl. Phys. 22, 1057–1062.CrossRefGoogle Scholar
Matsusaka, S., Maruyama, H., Matsuyama, T. & Ghadiri, M. 2010 Triboelectric charging of powders: a review. Chem. Engng Sci. 65, 5781–5807.CrossRefGoogle Scholar
Matsuyama, T., Ogu, M., Yamamoto, H., Marijnissen, J. C. M. & Scarlett, B. 2003 Impact charging experiments with single particles of hundred micrometre size. Powder Technol. 135–136, 14–22.CrossRefGoogle Scholar
Matsuyama, T. & Yamamoto, H. 1995 Electrification of single polymer particles by successive impacts with metal targets. IEEE Trans. Ind. Applics. 31, 1441–1445.CrossRefGoogle Scholar
McLaughlin, J. B. 1989 Aerosol particle deposition in numerically simulated channel flow. Phys. Fluids A 1, 1211–1224.CrossRefGoogle Scholar
Milici, B., De Marchis, M., Sardina, G. & Napoli, E. 2014 Effects of roughness on particle dynamics in turbulent channel flows: a DNS analysis. J. Fluid Mech. 739, 465–478.Google Scholar
Miura, T., Koyaguchi, T. & Tanaka, Y. 2002 Measurements of electric charge distribution in volcanic plumes at Sakurajima volcano, Japan. Bull. Volcanol. 64, 75–93.Google Scholar
Murata, Y. & Kittaka, S. 1979 Evidence of electron transfer as the mechanism of static charge generation by contact of polymers with metals. Japan. J. Appl. Phys. 18, 421.CrossRefGoogle Scholar
Nifuku, M. & Katoh, H. 2003 A study on the static electrification of powders during pneumatic transportation and the ignition of dust cloud. Powder Technol. 135–136, 234–242.CrossRefGoogle Scholar
Nomura, T., Satoh, T. & Masuda, H. 2003 The environment humidity effect on the tribo-charge of powder. Powder Technol. 135–136, 43–49.CrossRefGoogle Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aero. Sci. 14, 729–739.Google Scholar
Robins, E. S., Lowell, J. & Rose-Innes, A. C. 1980 The role of surface ions in the contact electrification of insulators. J. Electrostat. 8, 153–160.CrossRefGoogle Scholar
Schein, L. B. 1999 Recent advances in our understanding of toner charging. J. Electrostat. 46, 29–36.Google Scholar
Schiller, L. & Naumann, A. Z. 1933 A drag coefficient correlation. Z. Ver. Dtsch. Ing. 77, 318–320.Google Scholar
Schmid, H.-J. & Vogel, L. 2003 On the modelling of the particle dynamics in electro-hydrodynamic flow-fields: I comparison of eulerian and lagrangian modelling approach. Powder Technol. 135–136, 118–135.CrossRefGoogle Scholar
Shinbrot, T., LaMarche, K. & Glasser, B. J. 2006 Triboelectrification and razorbacks: geophysical patterns produced in dry grains. Phys. Rev. Lett. 96, 178002.Google Scholar
Shirakawa, Y., Ii, N., Yoshida, M., Takashima, R., Shimosaka, A. & Hidaka, J. 2008 Quantum chemical calculation of electron transfer at metal/polymer interfaces. J. Soc. Powder Technol. Jpn. 45, 366–372.Google Scholar
Soo, S. L. 1971 Dynamics of charged suspensions. In Topics in Current Aerosol Research, pp. 71–73. Pergamon.Google Scholar
Stiesch, G. 2003 Modeling Engine Spray and Combustion Processes. Springer.Google Scholar
Tanoue, K., Ema, A. & Masuda, H. 1999 Effect of material transfer and work hardening of metal surface on the current generated by impact of particle. J. Chem. Engng Japan 32, 544–548.Google Scholar
Tanoue, K., Tanaka, H., Kitano, H. & Masuda, H. 2001 Numerical simulation of tribo-electrification of particles in a gas–solid two-phase flow. Powder Technol. 118, 121–129.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar
Tsuji, Y., Morikawa, Y. & Shiomi, H. 1984 Ldv measurements of an air–solid two-phase flow in a vertical pipe. J. Fluid Mech. 139, 417–434.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 54, 39–48.Google Scholar
Wang, B. 2010 Inter-phase interaction in a turbulent, vertical channel flow laden with heavy particles. Part i: numerical methods and particle dispersion properties. Intl J. Heat Mass Transfer 53, 2506–2521.CrossRefGoogle Scholar
Watano, S. 2006 Mechanism and control of electrification in pneumatic conveying of powders. Chem. Engng Sci. 61, 2271–2278.CrossRefGoogle Scholar
Watano, S., Saito, S. & Suzuki, T. 2003 Numerical simulation of electrostatic charge in powder pneumatic conveying process. Powder Technol. 135–136, 112–117.Google Scholar
Wong, J., Kwok, P. C. L. & Chan, H.-K. 2015 Electrostatics in pharmaceutical solids. Chem. Engng Sci. 125, 225–237.Google Scholar
Yamamoto, H. & Scarlett, B. 1986 Triboelectric charging of polymer particles by impact. Part. Part. Syst. Charact. 3, 117–121.Google Scholar