Article contents
Dispersion in two-dimensional turbulent buoyant plumes
Published online by Cambridge University Press: 02 June 2015
Abstract
Using high-resolution imaging and dye studies, we investigate experimentally the mixing of a tracer by the eddies within a two-dimensional turbulent buoyant plume. Instantaneously, the plume consists of a series of eddies, and at each point along the centreline of the plume, the along-plume speed of the leading edge of the eddies 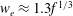 $w_{e}\approx 1.3f^{1/3}$, where
$w_{e}\approx 1.3f^{1/3}$, where 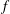 $f$ is the buoyancy flux, while the product of the length scale,
$f$ is the buoyancy flux, while the product of the length scale, 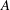 $A$, and frequency,
$A$, and frequency, 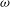 ${\it\omega}$, of the eddies
${\it\omega}$, of the eddies 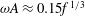 ${\it\omega}A\approx 0.15f^{1/3}$. The circulation and flow associated with the eddies lead to longitudinal mixing relative to the mean flow. To illustrate this mixing, we analyse the evolution of the horizontally averaged dye front produced by adding a constant flux of dye to a steady plume for times
${\it\omega}A\approx 0.15f^{1/3}$. The circulation and flow associated with the eddies lead to longitudinal mixing relative to the mean flow. To illustrate this mixing, we analyse the evolution of the horizontally averaged dye front produced by adding a constant flux of dye to a steady plume for times 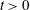 $t>0$. We show that the centre of mass of the horizontally averaged dye front has an along-plume speed
$t>0$. We show that the centre of mass of the horizontally averaged dye front has an along-plume speed 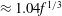 ${\approx}1.04f^{1/3}$. This is consistent with the predictions of a time-averaged model for the evolution of the horizontally averaged mass, momentum and buoyancy flux in the plume. The new data also show that the longitudinal spreading of the horizontally averaged dye front can be described in terms of a dispersivity
${\approx}1.04f^{1/3}$. This is consistent with the predictions of a time-averaged model for the evolution of the horizontally averaged mass, momentum and buoyancy flux in the plume. The new data also show that the longitudinal spreading of the horizontally averaged dye front can be described in terms of a dispersivity 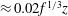 ${\approx}\,0.02f^{1/3}z$, where
${\approx}\,0.02f^{1/3}z$, where  $z$ is the vertical distance below the source. This model of longitudinal mixing enables calculation of the residence time distribution of material in the plume, which may be key to modelling the products of a reaction in which the reaction time is comparable to the travel time in the plume.
$z$ is the vertical distance below the source. This model of longitudinal mixing enables calculation of the residence time distribution of material in the plume, which may be key to modelling the products of a reaction in which the reaction time is comparable to the travel time in the plume.
JFM classification
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 14
- Cited by



