Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kukulka, T.
Plueddemann, A. J.
and
Sullivan, P. P.
2012.
Nonlocal transport due to Langmuir circulation in a coastal ocean.
Journal of Geophysical Research: Oceans,
Vol. 117,
Issue. C12,
Akan, Cigdem
Tejada-Martínez, Andrés E.
Grosch, Chester E.
and
Martinat, Guillaume
2013.
Scalar transport in large-eddy simulation of Langmuir turbulence in shallowwater.
Continental Shelf Research,
Vol. 55,
Issue. ,
p.
1.
Tejada-Martínez, Andrés E
Akan, Cigdem
Sinha, Nityanand
Grosch, Chester E
and
Martinat, Guillaume
2013.
Surface dynamics in LES of full-depth Langmuir circulation in shallow water.
Physica Scripta,
Vol. T155,
Issue. ,
p.
014008.
Li, Shuang
Li, Ming
Gerbi, Gregory P.
and
Song, Jin-Bao
2013.
Roles of breaking waves and Langmuir circulation in the surface boundary layer of a coastal ocean.
Journal of Geophysical Research: Oceans,
Vol. 118,
Issue. 10,
p.
5173.
Zhang, Jie
Tejada-Martínez, Andrés E.
and
Zhang, Qiong
2014.
Developments in computational fluid dynamics-based modeling for disinfection technologies over the last two decades: A review.
Environmental Modelling & Software,
Vol. 58,
Issue. ,
p.
71.
Martinat, Guillaume
Grosch, Chester E.
and
Gatski, Thomas B.
2014.
Modeling of Langmuir Circulation: Triple Decomposition of the Craik–Leibovich Model.
Flow, Turbulence and Combustion,
Vol. 92,
Issue. 1-2,
p.
395.
Sinha, Nityanand
Tejada-Martínez, Andres E.
Akan, Cigdem
and
Grosch, Chester E.
2015.
Toward a K-Profile Parameterization of Langmuir Turbulence in Shallow Coastal Shelves.
Journal of Physical Oceanography,
Vol. 45,
Issue. 12,
p.
2869.
Scully, Malcolm E.
Fisher, Alexander W.
Suttles, Steven E.
Sanford, Lawrence P.
and
Boicourt, William C.
2015.
Characterization and Modulation of Langmuir Circulation in Chesapeake Bay.
Journal of Physical Oceanography,
Vol. 45,
Issue. 10,
p.
2621.
Walker, Rachel
Tejada-Martínez, Andrés E.
and
Grosch, Chester E.
2016.
Large-Eddy Simulation of a Coastal Ocean under the Combined Effects of Surface Heat Fluxes and Full-Depth Langmuir Circulation.
Journal of Physical Oceanography,
Vol. 46,
Issue. 8,
p.
2411.
Golshan, Roozbeh
Tejada-Martínez, Andrés E.
Juha, Mario J.
and
Bazilevs, Yuri
2017.
LES and RANS simulation of wind- and wave-forced oceanic turbulent boundary layers in shallow water with wall modeling.
Computers & Fluids,
Vol. 142,
Issue. ,
p.
96.
Shrestha, Kalyan
Anderson, William
and
Kuehl, Joseph
2018.
Langmuir Turbulence in Coastal Zones: Structure and Length Scales.
Journal of Physical Oceanography,
Vol. 48,
Issue. 5,
p.
1089.
Scully, Malcolm E.
Trowbridge, John H.
Sherwood, Christopher R.
Jones, Katie R.
and
Traykovski, Peter
2018.
Direct Measurements of Mean Reynolds Stress and Ripple Roughness in the Presence of Energetic Forcing by Surface Waves.
Journal of Geophysical Research: Oceans,
Vol. 123,
Issue. 4,
p.
2494.
Fujiwara, Yasushi
Yoshikawa, Yutaka
and
Matsumura, Yoshimasa
2018.
A Wave-Resolving Simulation of Langmuir Circulations with a Nonhydrostatic Free-Surface Model: Comparison with Craik–Leibovich Theory and an Alternative Eulerian View of the Driving Mechanism.
Journal of Physical Oceanography,
Vol. 48,
Issue. 8,
p.
1691.
Trowbridge, John H.
and
Lentz, Steven J.
2018.
The Bottom Boundary Layer.
Annual Review of Marine Science,
Vol. 10,
Issue. 1,
p.
397.
Cao, Yu
Deng, Zengan
and
Wang, Chenxu
2019.
Impacts of surface gravity waves on summer ocean dynamics in Bohai Sea.
Estuarine, Coastal and Shelf Science,
Vol. 230,
Issue. ,
p.
106443.
Deng, Bing-Qing
Yang, Zixuan
Xuan, Anqing
and
Shen, Lian
2019.
Influence of Langmuir circulations on turbulence in the bottom boundary layer of shallow water.
Journal of Fluid Mechanics,
Vol. 861,
Issue. ,
p.
275.
Shrestha, K.
Anderson, W.
Tejada-Martinez, A.
and
Kuehl, J.
2019.
Orientation of coastal-zone Langmuir cells forced by wind, wave and mean current at variable obliquity.
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
p.
716.
Shrestha, Kalyan
and
Anderson, William
2020.
Coastal Langmuir circulations induce phase-locked modulation of bathymetric stress.
Environmental Fluid Mechanics,
Vol. 20,
Issue. 4,
p.
873.
Deng, Bing-Qing
Yang, Zixuan
Xuan, Anqing
and
Shen, Lian
2020.
Localizing effect of Langmuir circulations on small-scale turbulence in shallow water.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Peruzzi, C.
Vettori, D.
Poggi, D.
Blondeaux, P.
Ridolfi, L.
and
Manes, C.
2021.
On the influence of collinear surface waves on turbulence in smooth-bed open-channel flows.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
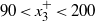 . The dependence of this disruption on wind and wave forcing conditions is investigated. Results indicate that the amount of disruption is primarily determined by the wavelength of the surface waves generating LC. These results have important implications for turbulence parameterizations for Reynolds-averaged Navier–Stokes simulations of the coastal ocean.
. The dependence of this disruption on wind and wave forcing conditions is investigated. Results indicate that the amount of disruption is primarily determined by the wavelength of the surface waves generating LC. These results have important implications for turbulence parameterizations for Reynolds-averaged Navier–Stokes simulations of the coastal ocean.