Published online by Cambridge University Press: 16 December 2010
In many turbulent flows near obstacles or in ducts, the turbulence is inhomogeneous in two directions perpendicular to the main flow direction. In convective flows, there may initially be no mean motion. In both types of flow the gradients of Reynolds stresses drive mean motions in directions of inhomogeneity. Using the method of rapid distortion theory developed by Hunt & Graham (J. Fluid Mech., vol. 84, 1978, p. 209), we analyse these gradients where homogeneous isotropic turbulence is impinging onto two semi-infinite flat rigid surfaces intersecting at right angles. The mean velocity is assumed to be uniform (i.e. the surfaces move at free-stream velocity, or the boundary layers are very thin). The inhomogeneous spectra, variances and Reynolds-stress gradients are evaluated. For isotropic free-stream turbulence with mean square velocity u2∞1, the mean square velocity fluctuation at a high Reynolds number in the corner is u21(X, 0, 0) = 2.121u2∞1, independent of the form of the spectrum. This is explained by estimating how the free-stream eddies are blocked by the two walls. The gradients of Reynolds stresses force a mean secondary flow to develop; its direction is into the corner, and its magnitude at time t is of order tu2∞1/L∞, where L∞ is the integral scale. These results are tested in a wind tunnel experiment. A turbulence-generating grid installed at the entrance to the test section generates nearly isotropic, grid-generated turbulence. A corner plate with faces parallel to the mean flow and sharp edges is placed downstream of the grid so that shear-free turbulence impinges onto the corner plate. The turbulent Reynolds number based on 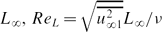 , is 1400 at the leading edge of the plate. A hot-wire anemometry is used to measure instantaneous velocities. The experimental results are consistent with the rapid distortion theory estimates for the variances and the secondary mean motion, which is in the same direction and has the same order of magnitude as Prandtl's analysis of shear-driven secondary flow (of the second kind). We conclude that the blocking mechanism adds to the shear effects and has a significant and sometimes dominant contribution to the crossflows wherever it acts in two non-parallel directions, such as convection in a corner. Consequently, mean transport into corners occurs for most kinds of distorted flow with weak viscous stresses, which has many engineering and environmental implications. There are also implications for the chaotic nature of many confined flows near corners.
, is 1400 at the leading edge of the plate. A hot-wire anemometry is used to measure instantaneous velocities. The experimental results are consistent with the rapid distortion theory estimates for the variances and the secondary mean motion, which is in the same direction and has the same order of magnitude as Prandtl's analysis of shear-driven secondary flow (of the second kind). We conclude that the blocking mechanism adds to the shear effects and has a significant and sometimes dominant contribution to the crossflows wherever it acts in two non-parallel directions, such as convection in a corner. Consequently, mean transport into corners occurs for most kinds of distorted flow with weak viscous stresses, which has many engineering and environmental implications. There are also implications for the chaotic nature of many confined flows near corners.
Present address: European Space Agency and AOES, Haagse Schouwweg 6G, Leiden, The Netherlands