Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T22:49:28.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and wall collision of inertial particles in a solid–liquid turbulent channel flow

Published online by Cambridge University Press:  25 October 2019

Masoud Ebrahimian ,
R. Sean Sanders  and
Sina Ghaemi Open the ORCID record for Sina Ghaemi [Opens in a new window]
Masoud Ebrahimian
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G1H9, Canada
R. Sean Sanders
Affiliation:
Department of Chemical and Materials Engineering, University of Alberta, Edmonton, Alberta T6G1H9, Canada
Sina Ghaemi*
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G1H9, Canada
*
†Email address for correspondence: ghaemi@ualberta.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics and wall collision of inertial particles were investigated in non-isotropic turbulence of a horizontal liquid channel flow. The inertial particles were 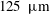$125~\unicode[STIX]{x03BC}\text{m}$ glass beads at a volumetric concentration of 0.03 %. The bead-laden flow and the unladen base case had the same volumetric flow rates, with a shear Reynolds number, 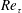$Re_{\unicode[STIX]{x1D70F}}$, of the unladen flow equal to 410 based on the half-channel height and friction velocity. Lagrangian measurements of three-dimensional trajectories of both fluid tracers and glass beads were obtained using time-resolved particle tracking velocimetry based on the shake-the-box algorithm of Schanz et al. (Exp. Fluids, vol. 57, no. 5, 2016, pp. 1–27). The analysis showed that on average the near-wall glass beads decelerate in the streamwise direction, while farther away from the wall, the streamwise acceleration of the glass beads became positive. The ejection motions provided a local maximum streamwise acceleration above the buffer layer by transporting glass beads to high velocity layers and exposing them to a high drag force in the streamwise direction. Conversely, the sweep motion made the maximum contribution to the average streamwise deceleration of glass beads in the near-wall region. The wall-normal acceleration of the beads was positive in the vicinity of the wall, and it became negative farther from the wall. The investigation showed that the glass beads with sweeping motion had the maximum momentum, streamwise deceleration, and wall-normal acceleration among all the beads close to the wall and these values increased with increasing their trajectory angle. The investigation of the beads that collided with the wall showed that those with shallow impact angles (less than 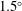$1.5^{\circ }$) typically slide along the wall. The sliding beads had a small streamwise momentum exchange of 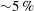${\sim}5\,\%$ during these events. The duration of their sliding motion could be as much as five times the inner time scale of the unladen flow. The wall-normal velocity of these beads after sliding was greater than their wall-normal velocity before sliding, and was associated with the rotation induced lift force. Beads with impact angles greater than 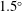$1.5^{\circ }$ had shorter interaction times with the wall and smaller streamwise and wall-normal restitution ratios.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 872 - 905
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmadi, F., Ebrahimian, M., Sanders, R. S. & Ghaemi, S. 2019 Particle image and tracking velocimetry of solid–liquid turbulence in a horizontal channel flow. Intl J. Multiphase Flow 112, 83–99.Google Scholar
Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Ayyalasomayajula, S., Gylfason, A., Collins, L. R., Bodenschatz, E. & Warhaft, Z. 2006 Lagrangian measurements of inertial particle accelerations in grid generated wind tunnel turbulence. Phys. Rev. Lett. 97, 144507.Google Scholar
Barros, D., Hiltbrand, B. & Longmire, E. K. 2018 Measurement of the translation and rotation of a sphere in fluid flow. Exp. Fluids 59 (6), 104.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.Google Scholar
Calzavarini, E., Volk, R., Lévêque, E., Pinton, J. F. & Toschi, F. 2012 Impact of trailing wake drag on the statistical properties and dynamics of finite-sized particle in turbulence. Physica D 241, 237–244.Google Scholar
Chen, L., Coleman, S. W., Vassilicos, J. C. & Hu, Z. 2010 Acceleration in turbulent channel flow. J. Turbul. 11, N41.Google Scholar
Crowe, C., Schwarzkopf, J., Sommerfeld, M. & Tsuji, Y. 2012 Multiphase Flows with Droplets and Particles. CRC Press.Google Scholar
Drew, D. A. & Passman, S. 1999 Theory of Multicomponent Fluids. Springer.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52, 309–329.Google Scholar
Elsinga, G. E., Scarano, F., Wieneke, B. & Van Oudheusden, B. W. 2006 Tomographic particle image velocimetry. Exp. Fluids 41 (6), 933–947.Google Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 277, 271–301.Google Scholar
Gerashchenko, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617, 255–281.Google Scholar
Gesemann, S., Huhn, F., Schanz, D. & Schröder, A. 2016 From noisy particle tracks to velocity, acceleration and pressure fields using B-splines and penalties. In 18th International Symposium on the Applications of Laser and Imaging Techniques to Fluid Mechanics (Lisbon, Portugal, 4–7 July), Springer.Google Scholar
Ghaemi, S. & Scarano, F. 2010 Multi-pass light amplification for tomographic particle image velocimetry applications. Meas. Sci. Technol. 21 (12), 127002.Google Scholar
Gondret, P., Lance, M. & Petit, L. 2002 Bouncing motion of spherical particles in fluids. Phys. Fluids 14, 643–652.Google Scholar
Hetsroni, G. 1989 Particles–turbulence interaction. Intl J. Multiphase Flow 15 (5), 735–746.Google Scholar
Joseph, G. G. & Hunt, M. L. 2004 Oblique particle–wall collisions in a liquid. J. Fluid Mech. 510, 71–93.Google Scholar
Joseph, G. G., Zenit, J. R., Hunt, M. L. & Rosenwinkel, A. M. 2001 Particle–wall collision in a viscous fluid. J. Fluid Mech. 433, 329–346.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995a Particle behavior in the turbulent boundary layer. I. Motion, deposition, and entrainment. Phys. Fluids 7, 1095–1106.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995b Particle behavior in the turbulent boundary layer. II. Velocity and distribution profiles. Phys. Fluids 7, 1107–1121.Google Scholar
Kiger, K. T. & Pan, C. 2002 Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 3, 1–17.Google Scholar
Kim, I., Elghobashi, E. & Sirignano, W. A. 1998 On the equation for spherical-particle motion: effect of Reynolds and acceleration numbers. J. Fluid Mech. 267, 221–253.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kim, J. & Balachandar, S. 2012 Mean and fluctuating components of drag and lift forces on an isolated finite-sized particle in turbulence. Theor. Comput. Fluid Dyn. 26, 185–204.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kosinski, P. & Hoffmann, A. C. 2009 Extension of the hard-sphere particle–wall collision model to account for particle deposition. Phys. Rev. E 79 (6), 061302.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Kussin, J. & Sommerfeld, M. 2002 Experimental studies on particle behaviour and turbulence modification in horizontal channel flow with different wall roughness. Exp. Fluids 33, 143–159.Google Scholar
Lavezzo, V., Soldati, A., Gerashchenko, S., Warhaft, Z. & Collins, L. R. 2010 On the role of gravity and shear on inertial particle accelerations in near-wall turbulence. J. Fluid Mech. 658, 229–246.Google Scholar
Lee, S. & Lee, C. 2005 Intermittency of acceleration in isotropic turbulence. Phys. Rev. E 71, 056310.Google Scholar
Lee, C., Yeo, K. & Choi, J. I. 2004 Intermittent nature of acceleration in near wall turbulence. Phys. Rev. Lett. 92, 144502.Google Scholar
Legendre, D., Zenit, R., Daniel, C. & Guiraud, P. 2006 A note on the modelling of the bouncing of spherical drops or solid spheres on a wall in viscous fluid. Chem. Engng Sci. 61 (11), 3543–3549.Google Scholar
Luo, K., Hu, C., Wu, F. & Fan, J. 2017 Direct numerical simulation of turbulent boundary layer with fully resolved particles at low volume fraction. Phys. Fluids 29 (5), 053301.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a non-uniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Mei, R. W. & Adrian, R. J. 1992 Flow past a sphere with an oscillation in the free stream velocity and unsteady drag at finite Reynolds number. J. Fluid Mech. 237, 323–341.Google Scholar
Meller, Y. & Liberzon, A. 2015 Particle–fluid interaction forces as the source of acceleration PDF invariance in particle size. Intl J. Multiphase Flow 76, 22–31.Google Scholar
Milojevié, D. 1990 Lagrangian stochastic-deterministic (LSD) predictions of particle dispersion in turbulence. Part. Part. Syst. Charact. 7, 181–190.Google Scholar
Montgomery, D. C. & Runger, G. C. 2002 Applied Statistics and Probability for Engineers, 3rd edn. Wiley.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.Google Scholar
Nasr, H. & Ahmadi, G. 2007 The effect of two-way coupling and inter-particle collisions on turbulence modulation in a vertical channel flow. Intl J. Heat Fluid Flow 28 (6), 1507–1517.Google Scholar
Nino, Y. & Garcia, M. H. 1996 Experiments on particle–turbulence interactions in the near-wall region of an open channel flow: implications for sediment transport. J. Fluid Mech. 326, 285–319.Google Scholar
Prandtl, L.1932 Recent results of turbulence research. Technical Memorandum 720, National Advisory Committee for Aeronautics.Google Scholar
Rubinow, S. I. & Keller, J. B. 1961 The transverse force on spinning sphere moving in a viscous fluid. J. Fluid Mech. 11, 447–459.Google Scholar
Salman, A. D., Verba, A., Lukenics, Z. & Szabo, M. 1989 Effects of Impact Velocity and Angle on Collision and Particle Velocity after Collision. Periodica Polytechnica.Google Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57, 1–27.Google Scholar
Schröder, A., Schanz, D., Michaelis, D., Cierpka, C., Scharnowski, S. & Kähler, C. J. 2015 Advances of PIV and 4D-PTV ‘shake-the-box’ for turbulent flow analysis – the flow over periodic hills. Flow Turbul. Combust. 95, 193–209.Google Scholar
Shao, X., Wu, T. & Yu, Z. 2012 Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number. J. Fluid Mech. 693, 319–344.Google Scholar
Shokri, R., Ghaemi, S., Nobes, D. S. & Sanders, R. S. 2017 Investigation of particle-laden turbulent pipe flow at high-Reynolds-number using particle image/tracking velocimetry (PIV/PTV). Intl J. Multiphase Flow 89, 136–149.Google Scholar
Soldati, A. 2005 Particles turbulence interactions in boundary layers. Z. Angew. Math. Mech. J. Appl. Math. Mech. 85, 683–699.Google Scholar
Sommerfeld, M. & Huber, N. 1999 Experimental analysis and modelling of particle–wall collisions. Intl J. Multiphase Flow 25, 1457–1489.Google Scholar
Sommerfeld, M. & Lain, S. 2018 Stochastic modelling for capturing the behaviour of irregular-shaped non-spherical particles in confined turbulent flows. Powder Technol. 332, 253–264.Google Scholar
Stelzenmuller, N., Polanco, J. I., Vignal, L., Vinkovic, I. & Mordant, N. 2017 Lagrangian acceleration statistics in a turbulent channel flow. Phys. Rev. Fluids 2 (5), 054602.Google Scholar
Stocchino, A. & Guala, M. 2005 Particle–wall collision in shear thinning fluids. Exp. Fluids 38 (4), 476–484.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Tsuji, Y., Morikawa, Y., Tanaka, T., Nakatsukasa, N. & Nakatani, M. 1987 Numerical simulation of gas–solid two-phase flow in a two-dimensional horizontal channel. Intl J. Multiphase Flow 13 (5), 671–684.Google Scholar
Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulations of isotropic turbulence. Phys. Fluids 11, 1208–1220.Google Scholar
Voth, G. A., La Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45, 549–556.Google Scholar
Wieneke, B. 2013 Iterative reconstruction of volumetric particle distribution. Meas. Sci. Technol. 24, 024008.Google Scholar
Yeo, K., Kim, B. G. & Lee, C. 2010 On the near-wall characteristics of acceleration in turbulence. J. Fluid Mech. 659, 405–419.Google Scholar
Yu, W., Vinkovic, I. & Buffat, M. 2016 Acceleration statistics of finite-size particles in turbulent channel flow in the absence of gravity. Flow Turbul. Combust. 96, 183–205.Google Scholar
Yu, Z., Lin, Z., Shao, X. & Wang, L. P. 2017 Effects of particle–fluid density ratio on the interactions between the turbulent channel flow and finite-size particles. Phys. Rev. E 96 (3), 033102.Google Scholar
Zamansky, R., Vinkovic, I. & Gorokhovski, M. 2011 Acceleration statistics of solid particles in turbulent channel flow. Phys. Fluids 23, 113304.Google Scholar