Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thiébaud, Marine
and
Misbah, Chaouqi
2013.
Rheology of a vesicle suspension with finite concentration: A numerical study.
Physical Review E,
Vol. 88,
Issue. 6,
Narsimhan, Vivek
Zhao, Hong
and
Shaqfeh, Eric S. G.
2013.
Coarse-grained theory to predict the concentration distribution of red blood cells in wall-bounded Couette flow at zero Reynolds number.
Physics of Fluids,
Vol. 25,
Issue. 6,
p.
061901.
Thiébaud, Marine
Shen, Zaiyi
Harting, Jens
and
Misbah, Chaouqi
2014.
Prediction of Anomalous Blood Viscosity in Confined Shear Flow.
Physical Review Letters,
Vol. 112,
Issue. 23,
Quaife, Bryan
and
Biros, George
2014.
High-volume fraction simulations of two-dimensional vesicle suspensions.
Journal of Computational Physics,
Vol. 274,
Issue. ,
p.
245.
Narsimhan, Vivek
Spann, Andrew P.
and
Shaqfeh, Eric S. G.
2014.
The mechanism of shape instability for a vesicle in extensional flow.
Journal of Fluid Mechanics,
Vol. 750,
Issue. ,
p.
144.
Kaoui, Badr
Jonk, Ruben J. W.
and
Harting, Jens
2014.
Interplay between microdynamics and macrorheology in vesicle suspensions.
Soft Matter,
Vol. 10,
Issue. 26,
p.
4735.
Spann, Andrew P.
Zhao, Hong
and
Shaqfeh, Eric S. G.
2014.
Loop subdivision surface boundary integral method simulations of vesicles at low reduced volume ratio in shear and extensional flow.
Physics of Fluids,
Vol. 26,
Issue. 3,
Abreu, David
Levant, Michael
Steinberg, Victor
and
Seifert, Udo
2014.
Fluid vesicles in flow.
Advances in Colloid and Interface Science,
Vol. 208,
Issue. ,
p.
129.
Minetti, Christophe
Podgorski, Thomas
Coupier, Gwennou
and
Dubois, Frank
2014.
Fully automated digital holographic processing for monitoring the dynamics of a vesicle suspension under shear flow.
Biomedical Optics Express,
Vol. 5,
Issue. 5,
p.
1554.
Gires, Pierre-Yves
Srivastav, Aparna
Misbah, Chaouqi
Podgorski, Thomas
and
Coupier, Gwennou
2014.
Pairwise hydrodynamic interactions and diffusion in a vesicle suspension.
Physics of Fluids,
Vol. 26,
Issue. 1,
Winkler, Roland G.
Fedosov, Dmitry A.
and
Gompper, Gerhard
2014.
Dynamical and rheological properties of soft colloid suspensions.
Current Opinion in Colloid & Interface Science,
Vol. 19,
Issue. 6,
p.
594.
de Loubens, C.
Deschamps, J.
Boedec, G.
and
Leonetti, M.
2015.
Stretching of capsules in an elongation flow, a route to constitutive law.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
Narsimhan, Vivek
Spann, Andrew P.
and
Shaqfeh, Eric S. G.
2015.
Pearling, wrinkling, and buckling of vesicles in elongational flows.
Journal of Fluid Mechanics,
Vol. 777,
Issue. ,
p.
1.
Avazmohammadi, Reza
and
Ponte Castañeda, Pedro
2015.
The rheology of non-dilute dispersions of highly deformable viscoelastic particles in Newtonian fluids.
Journal of Fluid Mechanics,
Vol. 763,
Issue. ,
p.
386.
Lamura, Antonio
and
Gompper, Gerhard
2015.
Rheological Properties of Sheared Vesicle and Cell Suspensions.
Procedia IUTAM,
Vol. 16,
Issue. ,
p.
3.
Rahimian, Abtin
Veerapaneni, Shravan K.
Zorin, Denis
and
Biros, George
2015.
Boundary integral method for the flow of vesicles with viscosity contrast in three dimensions.
Journal of Computational Physics,
Vol. 298,
Issue. ,
p.
766.
Bryngelson, Spencer H.
and
Freund, Jonathan B.
2016.
Capsule-train stability.
Physical Review Fluids,
Vol. 1,
Issue. 3,
Quaife, Bryan
and
Biros, George
2016.
Adaptive time stepping for vesicle suspensions.
Journal of Computational Physics,
Vol. 306,
Issue. ,
p.
478.
Yazdani, Alireza
Li, Xuejin
and
Karniadakis, George Em
2016.
Dynamic and rheological properties of soft biological cell suspensions.
Rheologica Acta,
Vol. 55,
Issue. 6,
p.
433.
Matsunaga, D.
Imai, Y.
Yamaguchi, T.
and
Ishikawa, T.
2016.
Rheology of a dense suspension of spherical capsules under simple shear flow.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
110.
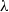 $\lambda $ is close to its critical value. Accordingly, in a non-dilute suspension the global minimum of the particle shear viscosity occurs at higher values of
$\lambda $ is close to its critical value. Accordingly, in a non-dilute suspension the global minimum of the particle shear viscosity occurs at higher values of 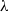 $\lambda $ due to the close correlation between the vesicle’s orientation and particle shear stress. In the high-
$\lambda $ due to the close correlation between the vesicle’s orientation and particle shear stress. In the high-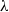 $\lambda $ regime, collisions in a suspension disrupt the TU cycles of individual vesicles, resulting in intermittent TU/TR motions. In addition, an entangled state is observed to occur for an interacting vesicle pair in the TR/TU regime, where the centroids are aligned approximately parallel to the vorticity direction and rotates about it. The persistence of this close-range interaction results in two distinct peaks in the pair distribution of vesicles. However, their existence is limited to suspensions at low volume fraction, as they are otherwise disrupted by the three-body interactions that occur more frequently in a dense suspension.
$\lambda $ regime, collisions in a suspension disrupt the TU cycles of individual vesicles, resulting in intermittent TU/TR motions. In addition, an entangled state is observed to occur for an interacting vesicle pair in the TR/TU regime, where the centroids are aligned approximately parallel to the vorticity direction and rotates about it. The persistence of this close-range interaction results in two distinct peaks in the pair distribution of vesicles. However, their existence is limited to suspensions at low volume fraction, as they are otherwise disrupted by the three-body interactions that occur more frequently in a dense suspension.