Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T17:19:27.519Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of a salinity gradient on the dissolution of a vertical ice face

Published online by Cambridge University Press:  24 February 2016

Craig D. McConnochie  and
Ross C. Kerr
Craig D. McConnochie*
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 2601, Australia
Ross C. Kerr
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 2601, Australia
*
†Email address for correspondence: craig.mcconnochie@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate experimentally the effect of stratification on a vertical ice face dissolving into cold salty water. We measure the interface temperature, ablation velocity and turbulent plume velocity over a range of salinity gradients and compare our measurements with results of similar experiments without a salinity gradient (Kerr & McConnochie, J. Fluid Mech., vol. 765, 2015, pp. 211–228; McConnochie & Kerr, J. Fluid Mech., vol. 787, 2016, pp. 237–253). We observe that stratification acts to reduce the ablation velocity, interface temperature, plume velocity and plume acceleration. 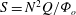We define a stratification parameter, $S=N^{2}Q/{\it\Phi}_{o}$, that describes where stratification will be important, where 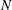$N$ is the Brunt–Väisälä frequency, 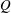$Q$ is the height-dependent plume volume flux and 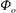${\it\Phi}_{o}$ is the buoyancy flux per unit area without stratification. The relevance of this stratification parameter is supported by our experiments, which deviate from the homogeneous theory at approximately 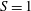$S=1$. Finally, we calculate values for the stratification parameter at a number of ice shelves and conclude that ocean stratification will have a significant effect on the dissolution of both the Antarctic and Greenland ice sheets.

JFM classification

Geophysical and Geological Flows: Ice sheets Convection: Plumes/thermals Phase change: Solidification/melting
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 589 - 607
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cooper, P. & Hunt, G. R. 2010 The ventilated filling box containing a vertically distributed source of buoyancy. J. Fluid Mech. 646, 39–58.CrossRefGoogle Scholar
Dowdeswell, J. A. & Bamber, J. L. 2007 Keel depths of modern Antarctic icebergs and implications for sea-floor scouring in the geological record. Mar. Geol. 243, 120–131.CrossRefGoogle Scholar
Huppert, H. E. & Josberger, E. G. 1980 The melting of ice in cold stratified water. J. Phys. Oceanogr. 10 (6), 953–960.2.0.CO;2>CrossRefGoogle Scholar
Huppert, H. E. & Turner, J. S. 1980 Ice blocks melting into a salinity gradient. J. Fluid Mech. 100 (2), 367–384.CrossRefGoogle Scholar
Jenkins, A., Dutrieux, P., Mcphail, S. D., Perrett, J. R., Webb, A. T. & White, D. 2010 Observations beneath Pine Island Glacier in West Antarctica and implications for its retreat. Nature Geosci. 3, 468–472.CrossRefGoogle Scholar
Jonassen, D. R., Settles, G. S. & Tronosky, M. D. 2006 Schlieren ‘PIV’ for turbulent flows. Opt. Lasers Engng 44 (3–4), 190–207.CrossRefGoogle Scholar
Josberger, E. G. & Martin, S. 1981 A laboratory and theoretical study of the boundary layer adjacent to a vertical melting ice wall in salt water. J. Fluid Mech. 111 (1), 439–473.CrossRefGoogle Scholar
Kerr, R. C. & McConnochie, C. D. 2015 Dissolution of a vertical solid surface by turbulent compositional convection. J. Fluid Mech. 765, 211–228.CrossRefGoogle Scholar
McConnochie, C. D. & Kerr, R. C. 2016 The turbulent wall plume from a vertically distributed source of buoyancy. J. Fluid Mech. 787, 237–253.CrossRefGoogle Scholar
Nokes, R.2014 Streams, version 2.03: system theory and design. Department of Civil and Natural Resources Engineering, University of Canterbury, New Zealand.Google Scholar
Oster, G. & Yanamoto, M. 1962 Density gradient techniques. Chem. Rev. 63 (3), 257–268.CrossRefGoogle Scholar
Rignot, E. & Jacobs, S. S. 2002 Rapid bottom melting widespread near Antarctic ice sheet grounding lines. Science 296 (5575), 2020–2023.CrossRefGoogle ScholarPubMed
Rignot, E., Velicogna, I., van den Broeke, M. R., Monaghan, A. & Lenaerts, J. T. M. 2011 Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 38, L05503.CrossRefGoogle Scholar
Robinson, N. J., Williams, M. J. M., Barrett, P. J. & Pyne, A. R. 2010 Observations of flow and ice–ocean interaction beneath the McMurdo Ice Shelf, Antarctica. J. Geophys. Res. 115, C03025.Google Scholar
Sutherland, D. A., Straneo, F. & Pickart, R. S. 2014 Characteristics and dynamics of two major Greenland glacial fjords. J. Geophys. Res. Oceans 119, 3767–3791.CrossRefGoogle Scholar
Venables, H. J. & Meredith, M. P. 2014 Feedbacks between ice cover, ocean stratification and heat content in Ryder Bay, western Antarctic Peninsula. J. Geophys. Res. Oceans 119, 5323–5336.CrossRefGoogle Scholar
Weast, R. C.(Ed.) 1989 CRC Handbook of Chemisty and Physics. CRC Press.Google Scholar
Williams, G. D., Hindell, M., Houssais, M.-N., Tamura, T. & Field, I. C. 2011 Upper ocean stratification and sea ice growth rates during the summer–fall transition, as revealed by elephant seal foraging in the Adélie Depression, East Antarctica. Ocean Sci. 7, 185–202.CrossRefGoogle Scholar
Woods, A. W. 1992 Melting and dissolving. J. Fluid Mech. 239, 429–448.CrossRefGoogle Scholar