Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T11:14:22.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of pressure gradient on the evolution of velocity-gradient tensor invariant dynamics on a controlled-diffusion aerofoil at $Re_{c}=150\,000$

Published online by Cambridge University Press:  17 April 2019

H. Wu Open the ORCID record for H. Wu [Opens in a new window] ,
S. Moreau Open the ORCID record for S. Moreau [Opens in a new window]  and
R. D. Sandberg Open the ORCID record for R. D. Sandberg [Opens in a new window]
H. Wu*
Affiliation:
Département de Génie Mécanique, Université de Sherbrooke, Sherbrooke, J1K 2R1, Canada
S. Moreau
Affiliation:
Département de Génie Mécanique, Université de Sherbrooke, Sherbrooke, J1K 2R1, Canada
R. D. Sandberg
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
*
†Email address for correspondence: hao.wu@usherbrooke.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

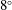A weakly compressible flow direct numerical simulation of a controlled-diffusion aerofoil at $8^{\circ }$ geometrical angle of attack, a chord-based Reynolds number of 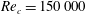$Re_{c}=150\,000$ and a Mach number of 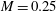$M=0.25$ based on the free-stream velocity relevant to many industrial applications was conducted to improve the understanding of the impact of the pressure gradient on the development of turbulent structures. The evolution equations for the two invariants 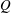$Q$ and 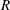$R$ of the velocity-gradient tensor have been studied at various locations along the aerofoil chord on its suction side. The shape of the mean evolution of the velocity-gradient tensor invariants were found to vary strongly when the flow encounters favourable, zero and adverse pressure gradients and as well for different wall-normal locations. The coupling between the pressure-Hessian tensor and the velocity-gradient tensor was found to be the major factor that causes these changes and is greatly influenced by the mean pressure-gradient condition and the wall-normal distance. Striking differences exist from the mean trajectories of this coupling at least in the log layer and outer layer subject to different mean pressure gradients. The nonlinearity and viscous diffusion effects keep their respective invariant characters regardless of the pressure-gradient effects and wall-normal locations. The wall and the mean adverse pressure gradient were both found to suppress the vortical stretching features of the flow. These features are of great importance for the development of future turbulence models on wall-bounded flows, especially on surfaces with significant curvature such as cambered aerofoils and blades for which significant mean pressure gradients exist.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 584 - 610
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. 1983 Analysis of a turbulent boundary layer subjected to a strong adverse pressure gradient. Intl J. Engng Sci. 21, 563–576.10.1016/0020-7225(83)90104-0Google Scholar
Bechlars, P.2015 Comprehensive characterisation of turbulence dynamics with emphasis on wall-bounded flows. PhD thesis, University of Southampton, Southampton.Google Scholar
Bechlars, P. & Sandberg, R. D. 2017a Evolution of the velocity gradient tensor invariant dynamics in a turbulent boundary layer. J. Fluid Mech. 815, 223–242.10.1017/jfm.2017.40Google Scholar
Bechlars, P. & Sandberg, R. D. 2017b Variation of enstrophy production and strain rotation relation in a turbulent boundary layer. J. Fluid Mech. 812, 321–348.10.1017/jfm.2016.794Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.10.1017/S0022112096001802Google Scholar
Bourassa, C. & Thomas, F. O. 2009 An experimental investigation of a highly accelerated turbulent boundary layer. J. Fluid Mech. 634, 359–404.10.1017/S0022112009007289Google Scholar
Carpenter, M. H., Nordström, J. & Gottlieb, D. 1999 A stable and conservative interface treatment of arbitrary spatial accuracy. J. Comput. Phys. 148, 341–365.10.1006/jcph.1998.6114Google Scholar
Chacín, J. M., Cantwell, B. J. & Kline, S. J. 1996 Study of turbulent boundary layer structure using the invariants of the velocity gradient tensor. Exp. Therm. Fluid Sci. 13, 308–317.10.1016/S0894-1777(96)00090-8Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.10.1017/S0022112097008057Google Scholar
Christophe, J.2011 Application of hybrid methods to high frequency aeroacoustics. PhD thesis, Université Libre de Bruxelles, Brussels.Google Scholar
Christophe, J., Anthoine, J. & Moreau, S. 2008 Trailing edge noise computation of a fan blade profile. ASA Paper 2008–3539.Google Scholar
Christophe, J., Anthoine, J. & Moreau, S.2009 Trailing edge noise of a controlled-diffusion airfoil at moderate and high angle of attack. AIAA Paper 2009-3196.10.2514/6.2009-3196Google Scholar
Christophe, J., Moreau, S., Hamman, C. W., Witteveen, J. A. S. & Iaccarino, G. 2014 Uncertainty quantification for the trailing-edge noise of a controlled-diffusion airfoil. AIAA J. 53, 42–54.10.2514/1.J051696Google Scholar
Clauser, F. H. 1956 The Turbulent Boundary Layer. Elsevier.10.1016/S0065-2156(08)70370-3Google Scholar
Deniau, H., Dufour, G., Boussuge, J. F., Polacsek, C. & Moreau, S.2011 Affordable compressible LES of airfoil–turbulence interaction in a free jet. AIAA Paper 2011-2707.10.2514/6.2011-2707Google Scholar
Gungor, A. G., Maciel, Y., Simens, M. P. & Soria, J.2014 Analysis of a turbulent boundary layer subjected to a strong adverse pressure gradient. J. Phys.: Conf. Ser. 506, 012007.Google Scholar
Hobbs, D. E. & Weingold, H. D. 1984 Development of controlled diffusion airfoils for multistage compressor application. Trans. ASME J. Engng Gas Turbines Power 106, 271–278.10.1115/1.3239559Google Scholar
Hosseini, S. M., Vinuesa, R., Schlatter, P., Hanifi, A. & Henningson, D. S. 2016 Direct numerical simulation of the flow around a wing section at moderate Reynolds number. Intl J. Heat Fluid Flow 61, 117–128.10.1016/j.ijheatfluidflow.2016.02.001Google Scholar
Indinger, T., Buschmann, M. H. & Gad-el Hak, M. 2006 Mean-velocity profile of turbulent boundary layers approaching separation. AIAA J. 44, 2465–2474.10.2514/1.18905Google Scholar
Istvan, M. S., Kurelek, J. W. & Yarusevych, S. 2017 Turbulence intensity effects on laminar separation bubbles formed over an airfoil. AIAA J. 56, 1335–1347.10.2514/1.J056453Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.10.1017/S0022112008000864Google Scholar
Joshi, P., Liu, X. & Katz, J. 2014 Effect of mean and fluctuating pressure gradients on boundary layer turbulence. J. Fluid Mech. 748, 36–84.10.1017/jfm.2014.147Google Scholar
Kennedy, C. A., Carpenter, M. H. & Lewis, R. M. 1999 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Maths 35, 177–219.10.1016/S0168-9274(99)00141-5Google Scholar
Kim, J. W. & Lee, D. J. 2003 Characteristic interface conditions for multiblock high-order computation on singular structured grid. AIAA J. 41, 2341–2348.10.2514/2.6858Google Scholar
Knopp, T., Schanz, D., Schröder, A., Dumitra, M., Cierpka, C., Hain, R. & Kähler, C. J. 2014 Experimental investigation of the log-law for an adverse pressure gradient turbulent boundary layer flow at Re 𝜃 = 10 000. Flow Turbul. Combust. 92, 451–471.10.1007/s10494-013-9479-3Google Scholar
Lee, J. H. & Sung, H. J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl J. Heat Fluid Flow 29, 568–578.10.1016/j.ijheatfluidflow.2008.01.016Google Scholar
Lee, J. H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.10.1017/S0022112009990814Google Scholar
Lissaman, P. B. S. 1983 Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 15, 223–239.10.1146/annurev.fl.15.010183.001255Google Scholar
Lozano-Durán, A., Holzner, M. & Jiménez, J. 2015 Numerically accurate computation of the conditional trajectories of the topological invariants in turbulent flows. J. Comput. Phys. 295, 805–814.10.1016/j.jcp.2015.04.036Google Scholar
Lumley, J. L. 1979 Computational modeling of turbulent flows. In Advances in Applied Mechanics, vol. 18, pp. 123–176. Elsevier.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.10.1146/annurev-fluid-122109-160708Google Scholar
Moreau, S., Henner, M., Iaccarino, G., Wang, M. & Roger, M. 2003 Analysis of flow conditions in freejet experiments for studying airfoil self-noise. AIAA J. 41, 1895–1905.Google Scholar
Moreau, S., Neal, D. R. & Foss, J. 2006 Hot-wire measurements around a controlled-diffusion airfoil in an open-jet anechoic wind tunnel. Trans. ASME J. Fluids Engng 128, 699–706.10.1115/1.2201644Google Scholar
Moreau, S. & Roger, M. 2005 Effect of airfoil aerodynamic loading on trailing edge noise sources. AIAA J. 43, 41–52.10.2514/1.5578Google Scholar
Nagano, Y., Tsuji, T. & Houra, T. 1998 Structure of turbulent boundary layer subjected to adverse pressure gradient. Intl J. Heat Fluid Flow 19, 563–572.10.1016/S0142-727X(98)10013-9Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.10.1063/1.3006423Google Scholar
Narasimha, R. & Sreenivasan, K. R. 1973 Relaminarization in highly accelerated turbulent boundary layers. J. Fluid Mech. 61, 417–447.10.1017/S0022112073000790Google Scholar
Neal, D. R.2010 The effects of rotation on the flow field over a controlled-diffusion airfoil. PhD thesis, Michigan State University, East Lansing, MI.Google Scholar
Nickels, T. B. 2004 Inner scaling for wall-bounded flows subject to large pressure gradients. J. Fluid Mech. 521, 217–239.10.1017/S0022112004001788Google Scholar
Ooi, A., Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.10.1017/S0022112098003681Google Scholar
Padois, T., Laffay, P., Idier, A. & Moreau, S.2015 Detailed experimental investigation of the aeroacoustic field around a controlled-diffusion airfoil. AIAA Paper 2015-2205.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125–155.10.1146/annurev.fl.19.010187.001013Google Scholar
Piomelli, U. & Yuan, J. 2013 Numerical simulations of spatially developing, accelerating boundary layers. Phys. Fluids 25, 101304.10.1063/1.4825033Google Scholar
Sandberg, R. D. 2015 Compressible-flow DNS with application to airfoil noise. Flow Turbul. Combust. 95, 211–229.10.1007/s10494-015-9617-1Google Scholar
Sandberg, R. D. & Sandham, N. D. 2006 Nonreflecting zonal characteristic boundary condition for direct numerical simulation of aerodynamic sound. AIAA J. 44, 402–405.10.2514/1.19169Google Scholar
Sanjosé, M., Moreau, S., Kim, M. S. & Pérot, F.2011 Direct self-noise simulation of the installed controlled diffusion airfoil. AIAA Paper 2011-2716.Google Scholar
Simonsen, A. J. & Krogstad, P. Å. 2005 Turbulent stress invariant analysis: clarification of existing terminology. Phys. Fluids 17, 088103.10.1063/1.2009008Google Scholar
Skaare, P. E. & Krogstad, P. Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.10.1017/S0022112094004489Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6, 871–884.10.1063/1.868323Google Scholar
Suman, S. & Girimaji, S. S. 2010 Velocity gradient invariants and local flow-field topology in compressible turbulence. J. Turbul. 11, 1–24.10.1080/14685241003604751Google Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Physica A 125, 150–162.10.1016/0378-4371(84)90008-6Google Scholar
Vinuesa, R., Örlü, R., Vila, C. S., Ianiro, A., Discetti, S. & Schlatter, P. 2017 Revisiting history effects in adverse-pressure-gradient turbulent boundary layers. Flow Turbul. Combust. 99, 565–587.10.1007/s10494-017-9845-7Google Scholar
von Kármán, T. H.1931 Mechanical similitude and turbulence, NACA Tech. Mem. 611.Google Scholar
Wang, L. & Lu, X. 2012 Flow topology in compressible turbulent boundary layer. J. Fluid Mech. 703, 255–278.10.1017/jfm.2012.212Google Scholar
Wang, M., Moreau, S., Iaccarino, G. & Roger, M. 2009 LES prediction of wall-pressure fluctuations and noise of a low-speed airfoil. Intl J. Aeroacoust. 8, 177–197.10.1260/147547208786940017Google Scholar
Wilcox, D. C. 1998 Turbulence Modeling for CFD. DCW Industries.Google Scholar
Winkler, J., Sandberg, R. D. & Moreau, S.2012 Direct numerical simulation of the self-noise radiated by an airfoil in a narrow stream. AIAA Paper 2012-2059.10.2514/6.2012-2059Google Scholar
Wu, H., Laffay, P., Idier, A., Jaiswal, P., Sanjosé, M. & Moreau, S. 2016 Numerical study of the installed controlled-diffusion airfoil at transitional Reynolds number. In Mathematical and Computational Approaches in Advancing Modern Science and Engineering, pp. 505–515. Springer.10.1007/978-3-319-30379-6_46Google Scholar
Wu, H., Sanjosé, M., Moreau, S. & Sandberg, R. D.2018 Direct numerical simulation of the self-noise radiated by the installed controlled-diffusion airfoil at transitional Reynolds number. AIAA Paper 2018-3797.10.2514/6.2018-3797Google Scholar
Wu, X., Moin, P., Wallace, J. M., Skarda, J., Lozano-Durán, A. & Hickey, J. P. 2017 Transitional–turbulent spots and turbulent–turbulent spots in boundary layers. Proc. Natl Acad. Sci. 114, E5292–E5299.10.1073/pnas.1704671114Google Scholar
Yuan, J. & Piomelli, U. 2015 Numerical simulation of a spatially developing accelerating boundary layer over roughness. J. Fluid Mech. 780, 192–214.10.1017/jfm.2015.437Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.10.1017/S002211209900467XGoogle Scholar