Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T05:57:52.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Efficient mixing in stratified flows: experimental study of a Rayleigh–Taylor unstable interface within an otherwise stable stratification

Published online by Cambridge University Press:  09 September 2014

Megan S. Davies Wykes  and
Stuart B. Dalziel
Megan S. Davies Wykes*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Stuart B. Dalziel
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: megan.davieswykes@cantab.net
Get access Rights & Permissions [Opens in a new window]

Abstract

Boussinesq salt-water laboratory experiments of Rayleigh–Taylor instability (RTI) can achieve mixing efficiencies greater than 0.75 when the unstable interface is confined between two stable stratifications. This is much greater than that found when RTI occurs between two homogeneous layers when the mixing efficiency has been found to approach 0.5. Here, the mixing efficiency is defined as the ratio of energy used in mixing compared with the energy available for mixing. If the initial and final states are quiescent then the mixing efficiency can be calculated from experiments by comparison of the corresponding density profiles. Varying the functional form of the confining stratifications has a strong effect on the mixing efficiency. 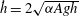We derive a buoyancy-diffusion model for the rate of growth of the turbulent mixing region, $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\dot{h} = 2 \sqrt{\alpha A g h}$ (where 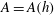$A = A(h)$ is the Atwood number across the mixing region when it extends a height 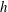$h$, $g$ is acceleration due to gravity and $\alpha $ is a constant). This model shows good agreement with experiments when the value of the constant $\alpha $ is set to 0.07, the value found in experiments of RTI between two homogeneous layers (where the height of the turbulent mixing region increases as 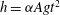$h =\alpha A g t^2$, an expression which is equivalent to that derived for 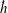$\dot{h}$).

JFM classification

Geophysical and Geological Flows: Stratified flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 1027 - 1057
Copyright
© British Crown owned copyright. Published by Cambridge University Press 2014. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allgayer, D. M. & Hunt, G. R. 2012 On the application of the light-attenuation technique as a tool for non-intrusive buoyancy measurements. Exp. Therm. Fluid Sci. 38, 257–261.Google Scholar
Alon, U., Hecht, J., Ofer, D. & Shvarts, D. 1995 Power laws and similarity of Rayleigh–Taylor and Richtmyer–Meshkov mixing fronts at all density ratios. Phys. Rev. Lett. 74, 534–537.Google Scholar
Andrews, M. J. & Dalziel, S. B. 2010 Small Atwood number Rayleigh–Taylor experiments. Phil. Trans. R. Soc. Ser. A 368 (1916), 1663–1679.Google Scholar
Boffetta, G., Mazzino, A., Musacchio, S. & Vozella, L. 2010 Rayleigh–Taylor instability in a viscoelastic binary fluid. J. Fluid Mech. 643, 127–136.Google Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type Ia supernovae. Nat. Phys. 2 (8), 562–568.Google Scholar
Cenedese, C. & Dalziel, S. B.1998 Concentration and depth fields determined by the light transmitted though a dyed solution. Exp. Fluids (submitted).Google Scholar
Cook, A. W., Cabot, W. H. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Dalziel, S. B. 1993 Rayleigh–Taylor instability: experiments with image analysis. Dyn. Atmos. Oceans 20 (1–2), 127–153.Google Scholar
Dalziel, S. B.1994 Molecular mixing in Rayleigh–Taylor instability. Tech. Rep.Google Scholar
Dalziel, S. B., Linden, P. F. & Youngs, D. L. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.Google Scholar
Dalziel, S. B., Patterson, M. D., Caulfield, C. P. & Coomaraswamy, I. A. 2008 Mixing efficiency in high-aspect-ratio Rayleigh–Taylor experiments. Phys. Fluids 20 (6), 065106.Google Scholar
Dimonte, G., Youngs, D. L., Dimits, A., Weber, S., Marinak, M., Wunsch, S., Garasi, C., Robinson, A., Andrews, M. J., Ramaprabhu, P., Calder, A. C., Fryxell, B., Biello, J., Dursi, L., MacNeice, P., Olson, K., Ricker, P., Rosner, R., Timmes, F., Tufo, H., Young, Y.-N. & Zingale, M. 2004 A comparative study of the turbulent Rayleigh–Taylor instability using high-resolution three-dimensional numerical simulations: the Alpha-Group collaboration. Phys. Fluids 16 (5), 1668–1693.Google Scholar
Glimm, J., Grove, J. W., Li, X. L., Oh, W. & Sharp, D. H. 2001 A critical analysis of Rayleigh–Taylor growth rates. J. Comput. Phys. 169 (2), 652–677.Google Scholar
Grinstein, F. F., Margolin, L. G. & Rider, W. J. 2007 Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics. Cambridge University Press.Google Scholar
Holford, J. M. & Dalziel, S. B. 1996 Measurements of layer depth during baroclinic instability in a two-layer flow. Appl. Sci. Res. 56 (2–3), 191–207.Google Scholar
Inogamov, N. A., Oparin, A. M., Dem’yanov, A. Y., Dembitskii, L. N. & Khokhlov, V. A. 2001 On stochastic mixing caused by the Rayleigh–Taylor instability. Sov. J. Exp. Theor. Phys. 92, 715–743.Google Scholar
Jacobs, J. W. & Dalziel, S. B. 2005 Rayleigh–Taylor instability in complex stratifications. J. Fluid Mech. 542 (1), 251.Google Scholar
Lawrie, A. G. W. & Dalziel, S. B. 2011a Rayleigh–Taylor mixing in an otherwise stable stratification. J. Fluid Mech. 688, 507–527.Google Scholar
Lawrie, A. G. W. & Dalziel, S. B. 2011b Turbulent diffusion in tall tubes. II. Confinement by stratification. Phys. Fluids 23 (8), 085110.Google Scholar
Linden, P. F., Redondo, J. M. & Youngs, D. L. 1994 Molecular mixing in Rayleigh–Taylor instability. J. Fluid Mech. 265, 97–124.Google Scholar
Lister, J. R., Kerr, R. C., Russell, N. J. & Crosby, A. 2011 Rayleigh–Taylor instability of an inclined buoyant viscous cylinder. J. Fluid Mech. 671, 313–338.Google Scholar
Lorenz, E. N. 1954 Available potential energy and the maintenance of the general circulation. Tellus 7 (2), 157–167.Google Scholar
Mueschke, N. J., Schilling, O., Youngs, D. L. & Andrews, M. J. 2009 Measurements of molecular mixing in a high-Schmidt-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 632, 17–48.Google Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes II: energetics of tidal and wind mixing. Deep-Sea Res. I 45 (12), 1977–2010.CrossRefGoogle Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.Google Scholar
Petrasso, R. D. 1994 Rayleigh’s challenge endures. Nat. Phys. 367 (6460), 217–218.Google Scholar
Prastowo, T., Griffiths, R. W., Hughes, G. O. & Hogg, A. McC. 2008 Mixing efficiency in controlled exchange flows. J. Fluid Mech. 600, 235–244.Google Scholar
Ramaprabhu, P. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.Google Scholar
Rayleigh, Lord 1900 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Sci. Papers 2, 200–207.Google Scholar
Read, K. I. 1984 Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12 (1–3), 45–58.Google Scholar
Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.Google Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor Instability. Physica D 12D, 3–18.Google Scholar
Snider, D. M. & Andrews, M. J. 1994 Rayleigh–Taylor and shear driven mixing with an unstable thermal stratification. Phys. Fluids 6 (10), 3324–3334.Google Scholar
Tailleux, R. 2009 Understanding mixing efficiency in the oceans: do the nonlinearities of the equation of state for seawater matter? Ocean Sci. 5, 271–283.Google Scholar
Tailleux, R. 2013 Available potential energy and exergy in stratified fluids. Annu. Rev. Fluid Mech. 45 (1), 35–58.Google Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. A 201 (1065), 192–196.Google Scholar
Tsiklashvili, V., Colio, P. E. R., Likhachev, O. & Jacobs, J. W. 2012 An experimental study of small Atwood number Rayleigh–Taylor instability using the magnetic levitation of paramagnetic fluids. Phys. Fluids 24 (5), 052106.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.CrossRefGoogle Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289 (1), 115–128.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36 (1), 281–314.Google Scholar
Youngs, D. L. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12 (1–3), 32–44.Google Scholar

Davies Wykes supplementary movie

Evolution of the mixing region in the upper layer when it is confined by a quadratic stratification with increasing density gradient.

Download Davies Wykes supplementary movie(Video)
Video 10.1 MB