Published online by Cambridge University Press: 22 May 2013
Pressure-driven squeezing of a concentrated emulsion of deformable drops through a randomly packed granular material is studied by rigorous three-dimensional multidrop–multiparticle simulations at low Reynolds numbers. The drops are comparable in size with granular particles, so the drop phase and the carrier fluid have different permeabilities, and the emulsion cannot be treated as single phase. Squeezing requires significant drop deformation and can meet much resistance, depending on the capillary number 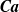 $\boldsymbol{Ca}$. The granular material is modelled as a random loose packing (RLP) of many highly-frictional rigid monodisperse spheres in a periodic cell in mechanical equilibrium. Flow simulations for many drops squeezing through the network of solid spheres are performed by an extension of the multipole-accelerated boundary-integral (BI) algorithm of Zinchenko & Davis (J. Comput. Phys., vol. 227, 2008, pp. 7841–7888). A major improvement is robust mesh control on drop surfaces combined with a novel fragmentation algorithm, now allowing for long-time simulations with intricate drop shapes and multiple breakups. A major challenge is that up to
$\boldsymbol{Ca}$. The granular material is modelled as a random loose packing (RLP) of many highly-frictional rigid monodisperse spheres in a periodic cell in mechanical equilibrium. Flow simulations for many drops squeezing through the network of solid spheres are performed by an extension of the multipole-accelerated boundary-integral (BI) algorithm of Zinchenko & Davis (J. Comput. Phys., vol. 227, 2008, pp. 7841–7888). A major improvement is robust mesh control on drop surfaces combined with a novel fragmentation algorithm, now allowing for long-time simulations with intricate drop shapes and multiple breakups. A major challenge is that up to 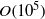 $O(1{0}^{5} )$ time steps are required in a simulation for time averaging, and
$O(1{0}^{5} )$ time steps are required in a simulation for time averaging, and 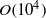 $O(1{0}^{4} )$ boundary elements per surface to sufficiently resolve lubrication and breakups. Such simulations are feasible due to multipole acceleration, with two orders-of-magnitude gain over the standard BI coding. For initial drop-to-particle size ratio 0.51–0.52, emulsion concentration 41–42 % in the available space, and matching viscosities, time- and ensemble-averaged permeabilities of the drop phase and the continuous phase are studied versus
$O(1{0}^{4} )$ boundary elements per surface to sufficiently resolve lubrication and breakups. Such simulations are feasible due to multipole acceleration, with two orders-of-magnitude gain over the standard BI coding. For initial drop-to-particle size ratio 0.51–0.52, emulsion concentration 41–42 % in the available space, and matching viscosities, time- and ensemble-averaged permeabilities of the drop phase and the continuous phase are studied versus 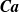 $\boldsymbol{Ca}$ for systems of different size (up to 36 particles and 100 drops in a periodic cell). An avalanche of drop breakups observed at sufficiently large
$\boldsymbol{Ca}$ for systems of different size (up to 36 particles and 100 drops in a periodic cell). An avalanche of drop breakups observed at sufficiently large 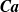 $\boldsymbol{Ca}$ does not preclude the permeabilities from reaching a statistical steady state in a feasible simulation time. The critical, system-size-independent
$\boldsymbol{Ca}$ does not preclude the permeabilities from reaching a statistical steady state in a feasible simulation time. The critical, system-size-independent 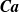 $\boldsymbol{Ca}$, when the drop-phase flow effectively stops due to blockage in the pores by capillary forces, is estimated from simulations. For a sample RLP configuration, deep distinctions are found between the flow of concentrated emulsions and single-drop motion.
$\boldsymbol{Ca}$, when the drop-phase flow effectively stops due to blockage in the pores by capillary forces, is estimated from simulations. For a sample RLP configuration, deep distinctions are found between the flow of concentrated emulsions and single-drop motion.