Article contents
Floquet stability analysis of capsules in viscous shear flow
Published online by Cambridge University Press: 13 August 2018
Abstract
Observations in experiments and simulations show that the kinematic behaviour of an elastic capsule, suspended and rotating in shear flow, depends upon the flow strength, the capsule membrane material properties and its at-rest shape. We develop a linear stability description of the periodically rotating base state of this coupled system, as represented by a boundary integral flow formulation with spherical harmonic basis functions describing the elastic capsule geometry. This yields Floquet multipliers that classify the stability of the capsule motion for elastic capillary numbers 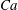 $Ca$ ranging from
$Ca$ ranging from 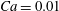 $Ca=0.01$ to 5. Viscous dissipation rapidly damps most perturbations. However, for all cases, a single component grows or decays slowly, depending upon
$Ca=0.01$ to 5. Viscous dissipation rapidly damps most perturbations. However, for all cases, a single component grows or decays slowly, depending upon 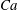 $Ca$, over many periods of the rotation. The transitions in this stability behaviour correspond to the different classes of rotating motion observed in previous studies.
$Ca$, over many periods of the rotation. The transitions in this stability behaviour correspond to the different classes of rotating motion observed in previous studies.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 2
- Cited by

