Flow phenomena in the very near wake of a flat plate with a circular trailing edge

Abstract

The very near wake of a flat plate with a circular trailing edge, exhibiting pronounced shedding of wake vortices, is investigated with data from direct numerical simulations (DNSs). Computations were performed for two cases. In the first case the Reynolds numbers based on plate length and thickness were 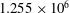$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1.255 \times 10^{6}$ and 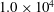$1.0 \times 10^{4}$, respectively. In the second case the two Reynolds numbers were 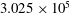$3.025 \times 10^{5}$ and 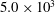$5.0 \times 10^{3}$, respectively. The separating boundary layers are turbulent and statistically identical thus resulting in a wake that is symmetric in the mean. The focus here is on the instability of the detached shear layers and the evolution of rib-vortex-induced localized regions of reverse flow. These regions detach from the main body of reverse flow in the trailing edge region and are convected downstream. The detached shear layers intermittently exhibit unstable behaviour, sometimes resulting in the development of shear-layer vortices as seen in earlier cylinder flow investigations with laminar separating boundary layers. Only a small fraction of the separated turbulent boundary layer experiences this instability, and also rolls up into the initial shed vortices. The instability causes a broadband peak in pressure spectra computed within the shear layers. Phase-averaged intensity and shear stress distributions of the randomly fluctuating component of velocity in the very near wake are also provided here and compared with those obtained in the near wake. The distributions of the production terms in the transport equations for the turbulent stresses are also provided.