Article contents
Forced synchronization and asynchronous quenching of periodic oscillations in a thermoacoustic system
Published online by Cambridge University Press: 01 February 2019
Abstract
We perform an experimental and theoretical study to investigate the interaction between an external harmonic excitation and a self-excited oscillatory mode (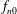 $f_{n0}$) of a prototypical thermoacoustic system, a horizontal Rijke tube. Such an interaction can lead to forced synchronization through the routes of phase locking or suppression. We characterize the transition in the synchronization behaviour of the forcing and the response signals of the acoustic pressure while the forcing parameters, i.e. amplitude (
$f_{n0}$) of a prototypical thermoacoustic system, a horizontal Rijke tube. Such an interaction can lead to forced synchronization through the routes of phase locking or suppression. We characterize the transition in the synchronization behaviour of the forcing and the response signals of the acoustic pressure while the forcing parameters, i.e. amplitude (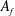 $A_{f}$) and frequency (
$A_{f}$) and frequency (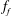 $f_{f}$) of forcing are independently varied. Further, suppression is categorized into synchronous quenching and asynchronous quenching depending upon the value of frequency detuning (
$f_{f}$) of forcing are independently varied. Further, suppression is categorized into synchronous quenching and asynchronous quenching depending upon the value of frequency detuning (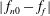 $|\,f_{n0}-f_{f}|$). When the applied forcing frequency is close to the natural frequency of the system, the suppression in the amplitude of the self-excited oscillation is known as synchronous quenching. However, this suppression is associated with resonant amplification of the forcing signal, leading to an overall increase in the response amplitude of oscillations. On the other hand, an almost 80 % reduction in the root mean square value of the response oscillation is observed when the system is forced for a sufficiently large value of the frequency detuning (only for
$|\,f_{n0}-f_{f}|$). When the applied forcing frequency is close to the natural frequency of the system, the suppression in the amplitude of the self-excited oscillation is known as synchronous quenching. However, this suppression is associated with resonant amplification of the forcing signal, leading to an overall increase in the response amplitude of oscillations. On the other hand, an almost 80 % reduction in the root mean square value of the response oscillation is observed when the system is forced for a sufficiently large value of the frequency detuning (only for 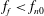 $f_{f}<f_{n0}$). Such a reduction in amplitude occurs due to asynchronous quenching where resonant amplification of the forcing signal does not occur, as the frequency detuning is significantly high. Further, the results from a reduced-order model developed for a horizontal Rijke tube show a qualitative agreement with the dynamics observed in experiments. The relative phase between the acoustic pressure (
$f_{f}<f_{n0}$). Such a reduction in amplitude occurs due to asynchronous quenching where resonant amplification of the forcing signal does not occur, as the frequency detuning is significantly high. Further, the results from a reduced-order model developed for a horizontal Rijke tube show a qualitative agreement with the dynamics observed in experiments. The relative phase between the acoustic pressure (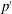 $p^{\prime }$) and the heat release rate (
$p^{\prime }$) and the heat release rate (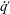 $\dot{q}^{\prime }$) oscillations in the model explains the occurrence of maximum reduction in the pressure amplitude due to asynchronous quenching. Such a reduction occurs when the positive coupling between
$\dot{q}^{\prime }$) oscillations in the model explains the occurrence of maximum reduction in the pressure amplitude due to asynchronous quenching. Such a reduction occurs when the positive coupling between 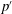 $p^{\prime }$ and
$p^{\prime }$ and 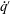 $\dot{q}^{\prime }$ is disrupted and their interaction results in overall acoustic damping, although both of them oscillate at the forcing frequency. Our study on the phenomenon of asynchronous quenching thus presents new possibilities to suppress self-sustained oscillations in fluid systems in general.
$\dot{q}^{\prime }$ is disrupted and their interaction results in overall acoustic damping, although both of them oscillate at the forcing frequency. Our study on the phenomenon of asynchronous quenching thus presents new possibilities to suppress self-sustained oscillations in fluid systems in general.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
Footnotes
Present address: Department of Mechanical Engineering, National Institute of Technology, Durgapur 713209, India. Email address for correspondence: sirshendumondal13@gmail.com
References
- 27
- Cited by



