Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T01:41:41.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Frequency spectra evolution of two-dimensional focusing wave groups in finite depth water

Published online by Cambridge University Press:  24 October 2011

Zhigang Tian ,
Marc Perlin  and
Wooyoung Choi
Zhigang Tian
Affiliation:
Division of Ocean Systems Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 305-701, Republic of Korea Naval Architecture & Marine Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Marc Perlin
Affiliation:
Naval Architecture & Marine Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Wooyoung Choi*
Affiliation:
Division of Ocean Systems Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 305-701, Republic of Korea Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102, USA
*
†Email address for correspondence: wychoi@njit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

An experimental and numerical study of the evolution of frequency spectra of dispersive focusing wave groups in a two-dimensional wave tank is presented. Investigations of both non-breaking and breaking wave groups are performed. It is found that dispersive focusing is far more than linear superposition, and that it undergoes strongly nonlinear processes. For non-breaking wave groups, as the wave groups propagate spatial evolution of wave frequency spectra, spectral bandwidth, surface elevation skewness, and kurtosis are examined. Nonlinear energy transfer between the above-peak (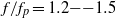) and the higher-frequency (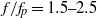) regions, with being the spectral peak frequency, is demonstrated by tracking the energy level of the components in the focusing and defocusing process. Also shown is the nonlinear energy transfer to the lower-frequency components that cannot be detected easily by direct comparisons of the far upstream and downstream measurements. Energy dissipation in the spectral peak region (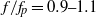) and the energy gain in the higher-frequency region (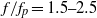) are quantified, and exhibit a dependence on the Benjamin–Feir Index (BFI). In the presence of wave breaking, the spectral bandwidth reduces as much as 40 % immediately following breaking and eventually becomes much smaller than its initial level. Energy levels in different frequency regions are examined. It is found that, before wave breaking onset, a large amount of energy is transferred from the above-peak region (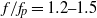) to the higher frequencies (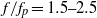), where energy is dissipated during the breaking events. It is demonstrated that the energy gain in the lower-frequency region is at least partially due to nonlinear energy transfer prior to wave breaking and that wave breaking may not necessarily increase the energy in this region. Complementary numerical studies for breaking waves are conducted using an eddy viscosity model previously developed by the current authors. It is demonstrated that the predicted spectral change after breaking agrees well with the experimental measurements.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave breaking
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 169 - 194
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baldock, T. E., Swan, C. & Taylor, P. H. 1996 A laboratory study of nonlinear surface waves on water. Phil. Trans. R. Soc. Lond. A 354, 649–676.Google Scholar
2. Banner, M. L. & Peirson, W. L. 2007 Wave breaking onset and strength for two-dimensional deep-water wave groups. J. Fluid Mech. 585, 93–115.CrossRefGoogle Scholar
3. Benjamin, T. B & Feir, J. E. 1967 Disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 27, 417–430.CrossRefGoogle Scholar
4. Choi, W. 1995 Nonlinear evolution equations for two-dimensional surface waves in a fluid of finite depth. J. Fluid Mech. 295, 381–394.CrossRefGoogle Scholar
5. Choi, W., Kent, C. P. & Schillinger, C. 2005 Numerical modelling of nonlinear surface waves and its validation. Adv. Engng Mech. 94–110.Google Scholar
6. Drazen, D. A., Melville, W. K. & Lenain, L. 2008 Inertial scaling of dissipation in unsteady breaking waves. J. Fluid Mech. 611, 307–332.Google Scholar
7. Duncan, J. H. 1981 An experimental investigation of breaking waves produced by a towed hydrofoil. Proc. R. Soc. Lond. Ser. A 377, 331–348.Google Scholar
8. Duncan, J. H. 1983 The breaking and non-breaking wave resistance of a two-dimensional hydrofoil. J. Fluid Mech. 126, 507–520.Google Scholar
9. Gemmrich, J. R., Banner, M. L. & Garrett, C. 2008 Spectrally resolved energy dissipation rate and momentum flux of breaking waves. J. Phys. Oceanogr. 38, 1296–1312.Google Scholar
10. Janssen, P. A. E. M. 2003 Nonlinear four-wave interaction and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.Google Scholar
11. Jiang, L., Perlin, M. & Schultz, W. W. 2004 Contact-line dynamics and damping for oscillating free surface flows. Phys. Fluids 16 (3), 748–758.CrossRefGoogle Scholar
12. Kway, J. H. L., Loh, Y. S. & Chan, E. S. 1998 Laboratory study of deep water breaking waves. Ocean Engng 25, 657–676.Google Scholar
13. Lake, B. M., Yuen, H. C., Rungaldier, H. & Ferguson, W. E. 1977 Nonlinear deep-water waves: theory and experiment. Part 2. Evolution of a continuous wave train. J. Fluid Mech. 83, 49–74.Google Scholar
14. Longuet-Higgins, M. S. 1983 On the joint distribution of wave periods and amplitudes in a random wave field. Proc. R. Soc. Lond. A. 389, 241–258.Google Scholar
15. Mei, C. C. 1983 The Applied Dynamics of Ocean Surface Waves. Wiley-Interscience.Google Scholar
16. Melville, W. K. 1982 The instability and breaking of deep-water waves. J. Fluid Mech. 115, 165–185.Google Scholar
17. Melville, W. K. 1994 Energy-dissipation by breaking waves. J. Phys. Oceanogr. 24, 2041–2049.Google Scholar
18. Melville, W. K. 1996 The role of surface-wave breaking in air–sea interaction. Annu. Rev. Fluid Mech. 28, 279–321.CrossRefGoogle Scholar
19. Melville, W. K., Veron, F. & White, C. J. 2002 The velocity field under breaking waves: coherent structures and turbulence. J. Fluid Mech. 454, 203–233.CrossRefGoogle Scholar
20. Meza, E., Zhang, J. & Seymour, R. J. 2000 Free-wave energy dissipation in experimental breaking waves. J. Phys. Oceanogr. 30, 2404–2418.2.0.CO;2>CrossRefGoogle Scholar
21. Nepf, H. M., Wu, C. H. & Chan, E. S. 1998 A comparison of two- and three-dimensional wave breaking. J. Phys. Oceanogr. 28, 1496–1510.Google Scholar
22. Ochi, M. K. 1998 Ocean waves: The stochastic approach.. Cambridge University Press.Google Scholar
23. Onorato, M., Cavaleri, L., Fouques, S., Gramstad, O., Janssen, P. A. E. M., Monbaliu, J., Osborne, A. R., Pakozdi, C., Serio, M., Stansberg, C. T., Toffoli, A. & Trulsen, K. 2009 Statistical properties of mechanically generated surface gravity waves: a laboratory experiment in a three-dimensional wave basin. J. Fluid Mech. 627, 235–257.Google Scholar
24. Perlin, M., He, J. H. & Bernal, L. P. 1996 An experimental study of deep water plunging breakers. Phys. Fluids 8 (9), 2365–2374.Google Scholar
25. Perlin, M. & Schultz, W. W. 2000 Capillary effects on surface waves. Annu. Rev. Fluid Mech. 32, 241–274.CrossRefGoogle Scholar
26. Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A. 331, 735–800.Google Scholar
27. Shemer, L., Goulitski, K. & Kit, E. 2007 Evolution of wide-spectrum unidirectional wave groups in a tank: an experimental and numerical study. Eur. J. Mech. (B/Fluids) 26, 193–219.CrossRefGoogle Scholar
28. Shemer, L. & Sergeeva, A. 2009 An experimental study of spatial evolution of statistical parameters in a unidirectional narrow-banded random wavefield. J. Geophys. Res. 114, C01015.Google Scholar
29. Song, J. B. & Banner, M. L. 2002 On determining the onset and strength of breaking for deep water waves. Part I: Unforced irrotational wave groups. J. Phys. Oceanogr. 32, 2541–2558.Google Scholar
30. Tian, Z. G., Perlin, M. & Choi, W. 2008 Evaluation of a deep-water wave breaking criterion. Phys. Fluids 20, 066604.Google Scholar
31. Tian, Z. G., Perlin, M. & Choi, W. 2010 Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J. Fluid Mech. 655, 217–257.Google Scholar
32. Tulin, M. P. & Waseda, T. 1999 Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 378, 197–232.CrossRefGoogle Scholar
33. West, B. J., Brueckner, K. A., Janda, R. S., Milder, D. M. & Milton, R. L. 1987 A new numerical method for surface hydrodynamics. J. Geophys. Res. 92 (11), 803-11–824.Google Scholar
34. Yao, A. F. & Wu, C. H. 2004 Energy dissipation of unsteady wave breaking on currents. J. Phys. Oceanogr. 34, 2288–2304.2.0.CO;2>CrossRefGoogle Scholar
35. Young, I. R. & Babanin, A. V. 2006 Spectral distribution of energy dissipation of wind-generated waves due to dominant wave breaking. J. Phys. Oceanogr. 36, 376–394.Google Scholar