Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T21:22:05.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth and instability of the liquid rim in the crown splash regime

Published online by Cambridge University Press:  09 July 2014

G. Agbaglah  and
R. D. Deegan
G. Agbaglah*
Affiliation:
Department of Physics and Centre for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA
R. D. Deegan
Affiliation:
Department of Physics and Centre for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: agbagla@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

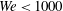We study the formation, growth and disintegration of jets following the impact of a drop on a thin film of the same liquid for $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{We}<1000$ and 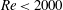$\mathit{Re}<2000$ using a combination of numerical simulations and linear stability theory (Agbaglah, Josserand & Zaleski, Phys. Fluids, vol. 25, 2013, 022103). Our simulations faithfully capture this phenomena and are in good agreement with experimental profiles obtained from high-speed X-ray imaging. We obtain scaling relations from our simulations and use these as inputs to our stability analysis. The resulting predictions for the most unstable wavelength are in excellent agreement with experimental data. Our calculations show that the dominant destabilizing mechanism is a competition between capillarity and inertia but that deceleration of the rim provides an additional boost to growth. We also predict over the entire parameter range of our study the number and timescale for formation of secondary droplets formed during a splash, based on the assumption that the most unstable mode sets the droplet number.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Interfacial Flows (free surface): Fingering instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 485 - 496
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbaglah, G., Delaux, S., Fuster, D., Hoepffner, J., Josserand, C., Popinet, S., Ray, P., Scardovelli, R. & Zaleski, S. 2011 Parallel simulation of multiphase flows using octree adaptivity and the volume-of-fluid method. C. R. Méc. 339, 194–207.CrossRefGoogle Scholar
Agbaglah, G., Josserand, C. & Zaleski, S. 2013 Longitudinal instability of a liquid rim. Phys. Fluids 25, 022103.CrossRefGoogle Scholar
Bremond, N. & Villermaux, E. 2006 Atomization by jet impact. J. Fluid Mech. 549, 273–306.CrossRefGoogle Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Coppola, G., Rocco, G. & de Luca, L. 2011 Insights on the impact of a plane drop on a thin liquid film. Phys. Fluids 23, 022105.Google Scholar
Cossali, G. E., Coghe, A. & Marengo, M. 1997 Impact of a single drop on a wetted solid surface. Exp. Fluids 22 (6), 463–472.CrossRefGoogle Scholar
Deegan, R. D., Brunet, P. & Eggers, J. 2008 Complexities of splashing. Nonlinearity 21 (1), C1–C11.Google Scholar
Fullana, J. M. & Zaleski, S. 1999 Stability of a growing end rim in a liquid sheet of uniform thickness. Phys. Fluids 11 (5), 952–954.CrossRefGoogle Scholar
Fuster, D., Agbaglah, G., Josserand, C., Popinet, S. & Zaleski, S. 2009 Numerical simulation of droplets, bubbles and waves: state of the art. Fluid Dyn. Res. 41 (6), 065001.CrossRefGoogle Scholar
Gueyffier, D. & Zaleski, S. 1998 Finger formation during droplet impact on a liquid film. C. R. Acad. Sci., Ser. IIb: Mec., Phys., Chim., Astron 326 (12), 839–844.Google Scholar
Krechetnikov, R. 2010 Stability of liquid sheet edges. Phys. Fluids 22, 092101.CrossRefGoogle Scholar
Krechetnikov, R. & Homsy, G. M. 2009 Crown-forming instability phenomena in the drop splash problem. J. Colloid Interface Sci. 331 (2), 555–559.Google Scholar
Liang, G., Guo, Y., Shen, S. & Yang, Y. 2014 Crown behavior and bubble entrainment during a drop impact on a liquid film. Theor. Comput. Fluid Dyn. 28, 159–170.Google Scholar
Popinet, S. 2003a Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190, 572–600.CrossRefGoogle Scholar
Popinet, S.2003b Gerris flow solver. http://gfs.sourceforge.net/.Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
Rieber, M. & Frohn, A. 1999 A numerical study on the mechanism of splashing. Intl J. Heat Fluid Flow 20 (5), 455–461.Google Scholar
Rioboo, R., Bauthier, C., Conti, J., Voue, M. & De Coninck, J. 2003 Experimental investigation of splash and crown formation during single drop impact on wetted surfaces. Exp. Fluids 35 (6), 648–652.Google Scholar
Roisman, I. V. 2010 On the instability of a free viscous rim. J. Fluid Mech. 661, 206–228.Google Scholar
Roisman, I. V., Gambaryan-Roisman, T., Kyriopoulos, O., Stephan, P. & Tropea, C. 2007 Breakup and atomization of a stretching crown. Phys. Rev. E 76 (2), 026302.Google Scholar
Roisman, I. V., Horvat, K. & Tropea, C. 2006 Spray impact: rim transverse instability initiating fingering and splash, and description of a secondary spray. Phys. Fluids 18 (10), 102104.CrossRefGoogle Scholar
Thoraval, M.-J., Takehara, K., Etoh, T. G., Popinet, S., Ray, P., Josserand, C., Zaleski, S. & Thoroddsen, S. T. 2012 von karman vortex street within an impacting drop. Phys. Rev. Lett. 108 (26), 264506.Google Scholar
Thoraval, M. J., Takehara, K., Etoh, T. G. & Thoroddsen, S. T. 2013 Drop impact entrapment of bubble rings. J. Fluid Mech. 724, 234–258.CrossRefGoogle Scholar
Worthington, A. M. 1879 On the spontaneous segmentation of a liquid annulus. Proc. Phys. Soc. Lond. 30, 49–60.Google Scholar
Yarin, A. L. & Weiss, D. A. 1995 Impact of drops on solid-surfaces—self-similar capillary waves, and splashing as a new-type of kinematic discontinuity. J. Fluid Mech. 283, 141–173.CrossRefGoogle Scholar
Zhang, L. V., Brunet, P., Eggers, J. & Deegan, R. D. 2010 Wavelength selection in the crown splash. Phys. Fluids 22 (12), 122105.Google Scholar
Zhang, L. V., Toole, J., Fezzaa, K. & Deegan, R. D. 2011 Evolution of the ejecta sheet from the impact of a drop with a deep pool. J. Fluid Mech. 396, 1–11.Google Scholar