Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T17:12:52.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Helicity dynamics in reconnection events of topologically complex vortex flows

Published online by Cambridge University Press:  11 June 2021

Xinran Zhao Open the ORCID record for Xinran Zhao [Opens in a new window]  and
Carlo Scalo Open the ORCID record for Carlo Scalo [Opens in a new window]
Xinran Zhao*
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN47907, USA
Carlo Scalo
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN47907, USA
*
†Email address for correspondence: zhao596@purdue.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

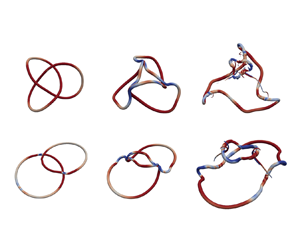
In this paper, we address the question of whether total helicity is conserved through viscous reconnection events in topologically complex vortex flows. To answer this question, we performed direct numerical simulations (DNS) focused on two complex vortex flow problems: (1) a trefoil knot and (2) a two-ring link, both simulated for various vortex core radii. The DNS framework relies on a block-structured adaptive mesh refinement (AMR) technique. A third simulation of a colliding pair of unlinked vortex rings, which exhibit no total helicity change, is also performed to serve as a reference case. The results show that a well-defined total helicity jump occurs during the unknotting/unlinking events of cases (1) and (2), which arises from the annihilation of the local helicity density content in the reconnection regions. Changes in total helicity become steeper as thinner core radii are considered for both cases (1) and (2). Finally, an analytical derivation based on the reconnection of two infinitesimal anti-parallel vortex filaments is provided that quantitatively links helicity annihilation and viscous circulation transfer processes, which unveils the fundamental hydrodynamic mechanisms responsible for production/destruction of total helicity during reconnection events.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex breakdown Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A30
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chichak, K.S., Cantrill, S.J., Pease, A.R., Chiu, S.-H., Cave, G.W.V., Atwood, J.L. & Stoddart, J.F. 2004 Molecular Borromean rings. Science 304 (5675), 1308–1312.CrossRefGoogle ScholarPubMed
Daryan, H., Hussain, F. & Hickey, J.-P. 2020 Aeroacoustic noise generation due to vortex reconnection. Phys. Rev. Fluids 5 (6), 062702.CrossRefGoogle Scholar
Dennis, M.R., King, R.P., Jack, B., O'Holleran, K. & Padgett, M.J. 2010 Isolated optical vortex knots. Nat. Phys. 6 (2), 118–121.CrossRefGoogle Scholar
Han, D., Pal, S., Liu, Y. & Yan, H. 2010 Folding and cutting dna into reconfigurable topological nanostructures. Nat. Nanotechnol. 5 (10), 712–717.CrossRefGoogle ScholarPubMed
Hoydonck, W.R.M., Van Bakker, R.J.J. & Van Tooren, M.J.L. 2010 A new method for rotor wake analysis using non-uniform rational b-spline primitives. Tech. Rep. NLR-TP-2010-465, National Aerospace Laboratory.Google Scholar
Hussain, F. & Duraisamy, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23 (2), 021701.CrossRefGoogle Scholar
Kedia, H., Kleckner, D., Scheeler, M.W. & Irvine, W.T.M. 2018 Helicity in superfluids: existence and the classical limit. Phys. Rev. Fluids 3 (10), 104702.CrossRefGoogle Scholar
Kerr, R.M. 2018 Trefoil knot timescales for reconnection and helicity. Fluid Dyn. Res. 50 (1), 011422.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H.K. 2014 Reconnection of skewed vortices. J. Fluid Mech. 751, 329–345.Google Scholar
Kleckner, D. & Irvine, W.T.M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9 (4), 253–258.CrossRefGoogle Scholar
Laing, C.E., Ricca, R.L. & De Witt, L.S. 2015 Conservation of writhe helicity under anti-parallel reconnection. Sci. Rep. 5 (1), 1–6.CrossRefGoogle ScholarPubMed
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Mcgavin, P. & Pontin, D.I. 2018 Vortex line topology during vortex tube reconnection. Phys. Rev. Fluids 3 (5), 054701.CrossRefGoogle Scholar
McGavin, P. & Pontin, D.I. 2019 Reconnection of vortex tubes with axial flow. Phys. Rev. Fluids 4 (2), 024701.CrossRefGoogle Scholar
Moffatt, H.K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35 (1), 117–129.CrossRefGoogle Scholar
Moffatt, H.K. 2017 Helicity–invariant even in a viscous fluid. Science 357 (6350), 448–449.CrossRefGoogle Scholar
Moffatt, H.K. & Kimura, Y. 2019 a Towards a finite-time singularity of the Navier–Stokes equations. Part 1. Derivation and analysis of dynamical system. J. Fluid Mech. 861, 930–967.CrossRefGoogle Scholar
Moffatt, H.K. & Kimura, Y. 2019 b Towards a finite-time singularity of the Navier–Stokes equations. Part 2. Vortex reconnection and singularity evasion. J. Fluid Mech. 870, R1.CrossRefGoogle Scholar
Moffatt, H.K. & Ricca, R.L. 1992 Helicity and the Călugăreanu invariant. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci. 439 (1906), 411–429.Google Scholar
Oberti, C. & Ricca, R.L. 2019 Influence of winding number on vortex knots dynamics. Sci. Rep. 9 (1), 1–9.CrossRefGoogle ScholarPubMed
Ricca, R.L., Samuels, D.C. & Barenghi, C.F. 1999 Evolution of vortex knots. J. Fluid Mech. 391, 29–44.CrossRefGoogle Scholar
Salman, H. 2017 Helicity conservation and twisted seifert surfaces for superfluid vortices. Proc. R. Soc. A: Math. Phys. Engng Sci. 473 (2200), 20160853.CrossRefGoogle ScholarPubMed
Scheeler, M.W., Kleckner, D., Proment, D., Kindlmann, G.L. & Irvine, W.T.M. 2014 Helicity conservation by flow across scales in reconnecting vortex links and knots. Proc. Natl Acad. Sci. 111 (43), 15350–15355.CrossRefGoogle ScholarPubMed
Tkalec, U., Ravnik, M., Čopar, S., Žumer, S. & Muševič, I. 2011 Reconfigurable knots and links in chiral nematic colloids. Science 333 (6038), 62–65.CrossRefGoogle ScholarPubMed
Van Rees, W.M., Hussain, F. & Koumoutsakos, P. 2012 Vortex tube reconnection at $Re = 10\ 000$. Phys. Fluids 24 (7), 075105.CrossRefGoogle Scholar
Vatistas, G.H., Kozel, V. & Mih, W.C. 1991 A simpler model for concentrated vortices. Exp. Fluids 11 (1), 73–76.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2019 Construction of knotted vortex tubes with the writhe-dependent helicity. Phys. Fluids 31 (4), 047101.CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2020 A physical model of turbulence cascade via vortex reconnection sequence and avalanche. J. Fluid Mech. 883, A51.CrossRefGoogle Scholar
Zhao, X. & Scalo, C. 2020 A compact-finite-difference-based numerical framework for adaptive-grid-refinement simulations of vortex-dominated flows. In AIAA Scitech 2020 Forum, p. 0810.Google Scholar
Zhao, X., Yu, Z., Chapelier, J.-B. & Scalo, C. 2021 Direct numerical and large-eddy simulation of trefoil knotted vortices. J. Fluid Mech. 910, A31.CrossRefGoogle Scholar

Zhao and Scalo supplementary movie 1

Movie 1: trefoil knot vortex

Download Zhao and Scalo supplementary movie 1(Video)
Video 7.6 MB

Zhao and Scalo supplementary movie 2

Movie 2: two-ring link vortex

Download Zhao and Scalo supplementary movie 2(Video)
Video 5.5 MB