Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T05:21:31.988Z Has data issue: false hasContentIssue false
  • English
  • Français

High Rayleigh number convection in a porous medium containing a thin low-permeability layer

Published online by Cambridge University Press:  05 September 2014

Duncan R. Hewitt ,
Jerome A. Neufeld  and
John R. Lister
Duncan R. Hewitt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Institute of Theoretical Geophysics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Jerome A. Neufeld
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Institute of Theoretical Geophysics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK Department of Earth Science, University of Cambridge, Cambridge CB2 3EQ, UK BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
John R. Lister
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Institute of Theoretical Geophysics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: drh39@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

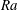Porous geological formations are commonly interspersed with thin, roughly horizontal, low-permeability layers. Statistically steady convection at high Rayleigh number $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ra}$ is investigated numerically in a two-dimensional porous medium that is heated at the lower boundary and cooled at the upper, and contains a thin, horizontal, low-permeability interior layer. In the limit that both the dimensionless thickness 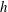$h$ and permeability 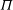$\Pi $ of the low-permeability layer are small, the flow is described solely by the impedance of the layer 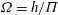$\Omega = h/\Pi $ and by 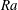$\mathit{Ra}$. In the limit 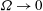$\Omega \to 0$ (i.e. 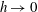$h \to 0$), the system reduces to a homogeneous Rayleigh–Darcy (porous Rayleigh–Bénard) cell. Two notable features are observed as 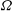$\Omega $ is increased: the dominant horizontal length scale of the flow increases; and the heat flux, as measured by the Nusselt number 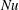$\mathit{Nu}$, can increase. For larger values of 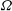$\Omega $, 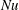$\mathit{Nu}$ always decreases. The dependence of the flow on 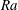$\mathit{Ra}$ is explored, over the range 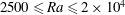$2500 \leqslant \mathit{Ra} \leqslant 2\times 10^4$. Simple one-dimensional models are developed to describe some of the observed features of the relationship 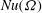$\mathit{Nu}(\Omega )$.

JFM classification

Convection: Convection Convection: Convection in porous media Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 844 - 869
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bachu, S. 2008 ${\mathrm{CO}}_2$ storage in geological media: role, means, status and barriers to deployment. Prog. Energy Combust. Sci. 34, 254–273.Google Scholar
Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106, 104501.Google Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. A. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.Google Scholar
Daniel, D., Tilton, N. & Riaz, A. 2013 Optimal perturbations of gravitationally unstable, transient boundary layers in porous media. J. Fluid Mech. 727, 456–487.Google Scholar
Ennis-King, J. P., Preston, I. & Paterson, L. 2005 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 84107–84115.Google Scholar
Friedlingstein, P., Houghton, R. A., Marland, G., Hackler, J., Boden, T. A., Conway, T. J., Canadell, J. G., Raupach, M. R., Ciais, P. & Le Quere, C. 2010 Update on ${\mathrm{CO}}_2$ emission. Nat. Geosci. 3, 811–812.Google Scholar
Genç, G. & Rees, D. A. S. 2011 The onset of convection in horizontally partitioned porous layers. Phys. Fluids 23, 064107.CrossRefGoogle Scholar
Gilfillan, S. M. V., Sherwood Lollar, B., Holland, G., Blagburn, D., Stevens, S., Schoell, M., Cassidy, M., Ding, Z., Zhou, Z., Lacrampe-Couloume, G. & Ballentine, C. J. 2009 Solubility trapping in formation water as dominant ${\mathrm{CO}}_2$ sinks in natural gas fields. Nature 458, 614–618.Google Scholar
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–89.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.Google Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.CrossRefGoogle Scholar
Kneafsey, T. J. & Pruess, K. 2010 Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Transp. Porous. Med. 82, 123–139.Google Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Math. Proc. Camb. Phil. Soc. 44, 508–521.Google Scholar
McKibbin, R. & O’Sullivan, M. J. 1980 Onset of convection in a layered porous medium heated from below. J. Fluid Mech. 96, 375–393.CrossRefGoogle Scholar
McKibbin, R. & O’Sullivan, M. J. 1981 Heat transfer in a layered porous medium heated from above. J. Fluid Mech. 111, 141–173.CrossRefGoogle Scholar
McKibbin, R. & Tyvand, P. A. 1983 Thermal convection in a porous medium composed of alternating thick and thin layers. Intl J. Heat Mass Transfer 26, 761–780.Google Scholar
Monkhouse, F. J. 1970 Principles of Physical Geography. University of London Press.Google Scholar
Morris, K. A. & Shepperd, C. M. 1982 The role of clay minerals in influencing porosity and permeability characteristics in the Bridport sands of Wytch Farm, Dorset. Clay Miner. 17, 41–54.CrossRefGoogle Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.CrossRefGoogle Scholar
Neufeld, J. A., Vella, D., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 1. A localized sink. J. Fluid Mech. 666, 391–413.Google Scholar
Nield, D. A. & Bejan, A. 2013 Convection in Porous Media, 4th edn. Springer.CrossRefGoogle Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in ${\mathrm{CO}}_2$ storage in saline aquifers. Adv. Water Resour. 33, 443–455.Google Scholar
Phillips, O. M. 2009 Geological Fluids Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. 1989 Numerical Recipes (Fortran), 1st edn. Cambridge University Press.Google Scholar
Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.Google Scholar
Rapaka, S., Pawar, R. J., Stauffer, P. H., Zhang, D. & Chen, S. 2009 Onset of convection over a transient base-state in anisotropic and layer porous media. J. Fluid Mech. 641, 227–244.Google Scholar
Rees, D. A. S. & Riley, D. S. 1990 The three-dimensional stability of finite-amplitude convection in a layered porous medium heated from below. J. Fluid Mech. 211, 437–461.Google Scholar
Riaz, A., Hesse, M. A., Tchelepi, H. A. & Orr, F. M. Jr 2006 Onset of convection in a gravitationally unstable diffusive layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Simmons, C. T., Fenstemaker, T. R. & Sharp, J. M. 2001 Variable-density groundwater flow and solute transport in heterogeneous porous media: approaches, resolutions and future challenges. J. Contam. Hydrol. 52, 245–275.Google Scholar
Slim, A. C. 2014 Solutal convection regimes in a two-dimensional porous medium. J. Fluid Mech. 741, 461–491.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.CrossRefGoogle Scholar
Sternlof, K. R., Karimi-Fard, M., Pollard, D. D. & Durlofsky, L. J. 2006 Flow and transport effects of compaction bands in sandstones at scales relevant to aquifer and reservoir management. Water Resour. Res. 42, W07425.CrossRefGoogle Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2013 Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315.Google Scholar
Tilton, N. & Riaz, A. 2014 Nonlinear stability of gravitationally unstable, transient, diffusive boundary layers in porous meda. J. Fluid Mech. 745, 251–278.Google Scholar
Vella, D., Neufeld, J. A., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 2. A line sink. J. Fluid Mech. 666, 414–427.Google Scholar
Zhang, W. 2013 Density-driven enhanced dissolution of injected ${\mathrm{CO}}_2$ during long-term ${\mathrm{CO}}_2$ storage. J. Earth Syst. Sci. 122, 1387–1397.Google Scholar