Published online by Cambridge University Press: 11 June 2013
The dynamics of horizontal convection are revealed by examining transient adjustment toward thermal equilibrium. We restrict attention to high Rayleigh numbers (of 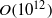 $O(1{0}^{12} )$) and a Prandtl number
$O(1{0}^{12} )$) and a Prandtl number 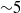 ${\sim }5$ that characterize many practical applications, and consider responses to small changes in the thermal boundary conditions, using laboratory experiments, three-dimensional direct numerical simulations (DNS) and simple theoretical models. The experiments and the mechanical energy budget from the DNS demonstrate that unsteady forcing can produce flow dramatically more active than horizontal convection under steady forcing. The physical mechanisms at work are indicated by the time scales of approach to the new equilibrium, and we show that these can range over two orders of magnitude depending on the imposed change in boundary conditions. Changes that lead to a net destabilizing buoyancy flux give rapid adjustments: for applied heat flux conditions the whole of the circulation is controlled by conduction through the stable portion of the boundary layer, whereas for applied temperature difference the circulation is controlled by small-scale convection within the unstable part of the boundary layer. The experiments, DNS and models are in close agreement and show that the time scale under applied temperatures is as small as 0.01 vertical diffusion time scales, a factor of four smaller than for imposed flux. Both cases give adjustments too rapid for diffusion in the interior to play a significant role, at least through 99 % of the adjustment, and we conclude that diffusion through the full depth is not significant in setting the equilibrium state. Boundary changes leading to a net stabilizing buoyancy flux give a very different response, causing the convection to quickly form a shallow circulation cell, followed eventually by a return to full-depth overturning through a combination of penetrative convection and conduction. The time scale again varies by orders of magnitude, depending on the boundary conditions and the location of the imposed boundary perturbation.
${\sim }5$ that characterize many practical applications, and consider responses to small changes in the thermal boundary conditions, using laboratory experiments, three-dimensional direct numerical simulations (DNS) and simple theoretical models. The experiments and the mechanical energy budget from the DNS demonstrate that unsteady forcing can produce flow dramatically more active than horizontal convection under steady forcing. The physical mechanisms at work are indicated by the time scales of approach to the new equilibrium, and we show that these can range over two orders of magnitude depending on the imposed change in boundary conditions. Changes that lead to a net destabilizing buoyancy flux give rapid adjustments: for applied heat flux conditions the whole of the circulation is controlled by conduction through the stable portion of the boundary layer, whereas for applied temperature difference the circulation is controlled by small-scale convection within the unstable part of the boundary layer. The experiments, DNS and models are in close agreement and show that the time scale under applied temperatures is as small as 0.01 vertical diffusion time scales, a factor of four smaller than for imposed flux. Both cases give adjustments too rapid for diffusion in the interior to play a significant role, at least through 99 % of the adjustment, and we conclude that diffusion through the full depth is not significant in setting the equilibrium state. Boundary changes leading to a net stabilizing buoyancy flux give a very different response, causing the convection to quickly form a shallow circulation cell, followed eventually by a return to full-depth overturning through a combination of penetrative convection and conduction. The time scale again varies by orders of magnitude, depending on the boundary conditions and the location of the imposed boundary perturbation.
Advection of passive dye tracer for the case of an applied temperature difference of 23.2˚C and a warming boundary perturbation applied at the heating end (a repeat of Run 14, table 1, and shown in figure 1). The clip shows the initial equilibrium flow and the more vigorous flow immediately after the boundary perturbation. The movie speed is 20 times actual speed in the laboratory and the clip shows a total of 14min of flow. The whole length of the box is shown. The clock at bottom reads zero until (at 9s from the beginning of the 42s clip) the heating temperature on the right hand half of the base is increased (by 3.9˚C) and the dye release is changed from red to blue. The flow has barely begun its long adjustment to the new boundary conditions by the end of this clip (where the clock reads 11min:17s). Once adjusted, this flow appeared indistinguishable from the initial equilibrated flow.
Advection of passive dye tracer for the case of an applied heat flux and a cooling boundary perturbation applied at the heating end (a repeat of Run 6, table 1, and shown in figure 5). The clip shows 3min of the initial equilibrium flow followed the early shutdown of deep convection to form a shallow circulation cell immediately after the applied heat flux was decreased by 10%. The movie speed is 20 times actual speed in the laboratory and approximately 60% of the box length is shown. The clock at bottom reset to zero (at 9s from the beginning of the 42s clip). A 7min interval has been removed from the middle of the clip (6min:30s to 13min:40s after the boundary perturbation), during which a few Potassium Permanganate crystals were dropped into the box and settled on the base to give up the purple tracer. After a long adjustment to the new boundary conditions the full-depth convection was re-established and the flow appeared indistinguishable from the initial equilibrium state.
Advection of passive dye tracer for the case of an applied heat flux and a cooling boundary perturbation in the temperature Tc applied at the cooling end (a repeat of Run 9, table 1, and shown in figure 6). The movie speed is 20 times actual speed in the laboratory and begins at the time the boundary temperature perturbation was applied. The clock at bottom was reset to zero at this time and the boundary proceeded to take 1 to 2 min to reach its new temperature. Approximately 60% of the box length is shown. The clip shows five separate periods: t=0 to 11min:48s, t = 54min:20s to 59min:45s, t = 4hrs:30min to 4hrs:44min, t = 9hrs:6min to 9hrs:12min, and t = 20hrs:58min to 21hrs:4min. New dye releases provided tracer for each time segment. In the final segment the flow is fully adjusted to the new boundary conditions and is indistinguishable from the initial equilibrium state.
A DNS solution (Run DNSb, table 1) showing the horizontal velocity field u(x, z) on the spanwise (y) mid-plane of the box for an increase in the temperature of the heating half of the base . The solution begins with the thermally equilibrated solution under the initial boundary conditions. The temperature of the heated (left hand) half of the base is then changed increased instantaneously. Immediately after this change the flow is far from equilibrium and velocities are very much larger than in equilibrium states. As the flow evolves toward equilibrium under the new boundary conditions, the velocities slowly decay back toward a solution close to the initial flow. Note that the velocity colour scale in the movie is held constant, whereas a varying colour scale is used in the instantaneous fields shown in figure 12.