Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:11:05.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypersonic flow over spherically blunted cone capsules for atmospheric entry. Part 1. The sharp cone and the sphere

Published online by Cambridge University Press:  03 June 2019

H. G. Hornung Open the ORCID record for H. G. Hornung [Opens in a new window] ,
Jan Martinez Schramm  and
Klaus Hannemann
H. G. Hornung*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
Jan Martinez Schramm
Affiliation:
Spacecraft Department, Institute of Aerodynamics and Flow Technology, German Aerospace Center, 37073 Göttingen, Germany
Klaus Hannemann
Affiliation:
Spacecraft Department, Institute of Aerodynamics and Flow Technology, German Aerospace Center, 37073 Göttingen, Germany
*
†Email address for correspondence: hans@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Depending on the cone half-angle and the inverse normal-shock density ratio $\unicode[STIX]{x1D700}$, hypersonic flow over a spherically blunted cone exhibits two regimes separated by an almost discontinuous jump of the body end of the sonic line from a point on the spherical nose to the shoulder of the cone, here called sphere behaviour and cone behaviour. The inflection point of the shock wave in sphere behaviour is explained. In Part 1 we explore the two elements of the capsule shape, the sphere and the sharp cone with detached shock, theoretically and computationally, in order to put the treatment of the full capsule shape on a sound basis. Starting from the analytical expression for the shock detachment angle of a cone given by Hayes & Probstein (Hypersonic Flow Theory, 1959, Academic Press) we make a hypothesis for the sharp cone, about the functional form of the dependence of dimensionless quantities on $\unicode[STIX]{x1D700}$ and a cone angle parameter, 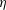$\unicode[STIX]{x1D702}$. In the critical part of atmospheric entry the shock shape and drag of the capsule are insensitive to viscous effects, so that much can be learned from inviscid studies. Accordingly, the hypothesis is tested by making a large number of Euler computations to cover the parameter space: Mach number, specific heat ratio and cone angle. The results confirm the hypothesis in the case of the dimensionless shock stand-off distance as well as for the drag coefficient, yielding accurate analytical functions for both. This reduces the number of independent parameters of the problem from three to two. A functional form of the shock stand-off distance is found for the transition from the 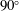$90^{\circ }$ cone to the sphere. Although the analysis assumes a calorically perfect gas, the results may be carried over to the high-enthalpy real-gas situation if the normal-shock density ratio is replaced by the density ratio based on the average density along the stagnation streamline (see e.g. Stulov, Izv. AN SSSR Mech. Zhidk. Gaza, vol. 4, 1969, pp. 142–146; Hornung, J. Fluid Mech., vol. 53, 1972, pp. 149–176; Wen & Hornung, J. Fluid Mech., vol. 299, 1995, pp. 389–405).

JFM classification

Compressible Flows: Gas dynamics Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 1097 - 1116
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braun, R. D., Powell, R. W., Cruz, C. I., Gnoffo, P. A. & Weilmuenster, K. J. 1995 Mars Pathfinder six-degree-of-freedom entry analysis. J. Spacecr. Rockets 36, 993–1000.Google Scholar
Desai, P. N. & Cheatwood, F. M. 2001 Entry dispersion analysis for the genesis sample return capsule. J. Spacecr. Rockets 38, 345–350.Google Scholar
Dyakonov, A. A., Schoeneberger, M. & Norman, J. W. 2012 Hypersonic and supersonic static aerodynamics of Mars Science Laboratory entry vehicle. In 43rd AIAA Thermophysics Conference, New Orleans, LA. AIAA Paper 2012-2999.Google Scholar
Edquist, K. 2006 Computations of Viking Lander capsule hypersonic aerodynamics with comparisons to ground and flight data. In AIAA Atmospheric Flight Mechanics Conference and Exhibit, Guidance, Navigation, and Control, Keystone, Colorado. AIAA Paper 2006-6137.Google Scholar
Einfeldt, B. 1988 On Godunov-type methods for gas dynamics. SIAM J. Numer. Anal. 25, 294–318.Google Scholar
Freeman, N. C. 1960 On a singular point in the Newtonian theory of hypersonic flow. J. Fluid Mech. 8, 109–122.Google Scholar
Gnoffo, P. A., Braun, R. D., Weilmuenster, K. J., Mitcheltree, R. A., Engelund, W. C. & Powell, R. W. 1999 Prediction and validation of Mars Pathfinder hypersonic aerodynamic database. J. Spacecr. Rockets 36, 367–373.Google Scholar
Gnoffo, P. A., Weilmuenster, K. J., Braun, R. D. & Cruz, C. I. 1996 Influence of sonic line location on Mars Pathfinder Probe aerodynamics. J. Spacecr. Rockets 33, 169–177.Google Scholar
Harten, A., Lax, P. D. & van Leer, B. 1983 On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 25, 35–61.Google Scholar
Hayes, W. D. & Probstein, R. F. 1959 Hypersonic Flow Theory. Academic Press.Google Scholar
Holden, M. S., Wadhams, T. P., MacLean, M. & Mundy, E. 2007 Experimental studies in LENS I and X to evaluate real gas effects on hypervelocity vehicle performance. In 45th AIAA Aerospace Sciences Meeting and Exhibit. AIAA Paper 2007-204.Google Scholar
Hornung, H. G. 1969 Some aspects of hypersonic flow over power-law bodies. J. Fluid Mech. 39, 143–162.Google Scholar
Hornung, H. G. 1972 Non-equilibrium flow of nitrogen over spheres and circular cylinders. J. Fluid Mech. 53, 149–176.Google Scholar
Ishii, N., Yamada, T., Hiraki, K. & Inatanii, Y. 2008 Reentry motion and aerodynamics of the MUSES-C sample return capsule. Trans. Japan Soc. Aero. Space Sci. 51, 65–70.Google Scholar
Krasil’nikov, A. V., Nikulin, A. N. & Kholodov, A. S. 1975 Some features of flow over spherically blunted cones of large vertex angles. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 2, 179–181.Google Scholar
Krasnov, N. F. 1970 Aerodynamics of Bodies of Revolution, chap. VII, equation (20.43). Rand Corporation.Google Scholar
Leibowitz, M. G. & Austin, J. M. 2019 Hypervelocity spherically-blunted cone flows in Mars entry ground testing. AIAA J. submitted.Google Scholar
Mitcheltree, R. A., Wilmoth, R. G., Cheatwood, F. M., Brauckmann, G. J. & Greene, F. A. 1997 Aerodynamics of Stardust sample return capsule. In AIAA Conference. AIAA Paper 97-2304.Google Scholar
Perminov, V. G. 1999 The Difficult Road to Mars – A Brief History of Mars Exploration in the Soviet Union, Monographs in Aerospace History, No. 15. NASA.Google Scholar
Powell, R. W., Justus, C. G., Bose, D., Chen, Y. K., Cruz, J. R., Duvall, A., Fisher, J., Hollis, B., Lockwood, M. K., Keller, V. et al. 2005 Independent technical assessment of Cassini/Huygens, probe entry, descent and landing at Titan. Tech. Rep. RP-05-67, NASA Engineering and Safety Center.Google Scholar
Pullin, D. I. 1980 Direct simulation methods for compressible inviscid ideal-gas flows. J. Comput. Phys. 34, 231–240.Google Scholar
Quirk, J. J. 1994 A contribution to the great Riemann solver debate. Intl J. Numer. Meth. Fluids 18, 555–574.Google Scholar
Quirk, J. J. 1998 Amrita – a computational facility (for CFD modelling). In VKI CFD, Lecture Series, vol. 29. Von Karman Institute.Google Scholar
Quirk, J. J. & Karni, S. 1996 On the dynamics of a shock bubble interaction. J. Fluid Mech. 318, 129–163.Google Scholar
Schoeneberger, M., Cheatwood, F. M. & Desai, P. W. 2005 Static aerodynamics of the Mars Exploration Rover entry capsule. In 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV. AIAA Paper 2005-0056.Google Scholar
Sharma, M., Swantek, A. B., Flaherty, W. & Austin, J. M. 2010 Experimental and numerical investigation of hypervelocity flow over blunt bodies. J. Thermophys. Heat Transfer 24, 673–683.Google Scholar
Solomon, G. E.1953 Transonic flow past cone-cylinders. Tech. Rep. 1242, NACA.Google Scholar
South, J. C. Jr. 1968 Calculation of axisymmetric supersonic flow past blunt bodies with sonic corners, including a program description and listing. Tech. Rep. NASA TN-D-4563, NASA.Google Scholar
Spencer, D. A., Thurman, S. W., Peng, C.-Y., Blanchard, R. C. & Braun, R. D.1998 Mars Path-finder atmospheric entry reconstruction. Tech. Rep. AAS Paper 98-146, American Astronautical Society.Google Scholar
Stulov, V. P. 1969 Similarity law for supersonic flow past blunt bodies. Izv. AN SSSR Mech. Zhidk. Gaza 4, 142–146.Google Scholar
Taylor, G. I. & Maccoll, J. W. 1933 The air pressure on a cone moving at high speed. Proc. R. Soc. Lond. A 139, 278–311.Google Scholar
Tran, P. & Beck, J.2011 EXOMARS Entry Demonstrator Module aerodynamics. Tech. Rep. ESASP.692E. European Space Agency.Google Scholar
Traugott, S. C. 1962 Some features of supersonic and hypersonic flow about blunted cones. J. Aero. Sci. 29, 389–399.Google Scholar
Wen, C.-Y. & Hornung, H. G. 1995 Non-equilibrium dissociating flow over spheres. J. Fluid Mech. 299, 389–405.Google Scholar
Wright, M. J., Olejniczak, J., Brown, J. L., Hornung, H. G. & Edquist, K. T.2005 Computational modeling of T5 laminar and turbulent heating data on blunt cones, part 2. AIAA Paper 2005-177.Google Scholar