Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T06:46:10.493Z Has data issue: false hasContentIssue false
  • English
  • Français

Importance of the nozzle-exit boundary-layer state in subsonic turbulent jets

Published online by Cambridge University Press:  19 July 2018

Guillaume A. Brès Open the ORCID record for Guillaume A. Brès [Opens in a new window] ,
Peter Jordan Open the ORCID record for Peter Jordan [Opens in a new window] ,
Vincent Jaunet ,
Maxime Le Rallic ,
André V. G. Cavalieri ,
Aaron Towne Open the ORCID record for Aaron Towne [Opens in a new window] ,
Sanjiva K. Lele ,
Tim Colonius  and
Oliver T. Schmidt Open the ORCID record for Oliver T. Schmidt [Opens in a new window]
Guillaume A. Brès*
Affiliation:
Cascade Technologies Inc., Palo Alto, CA 94303, USA
Peter Jordan
Affiliation:
Institut PPRIME, CNRS-Université de Poitiers-ENSMA, Poitiers, France
Vincent Jaunet
Affiliation:
Institut PPRIME, CNRS-Université de Poitiers-ENSMA, Poitiers, France
Maxime Le Rallic
Affiliation:
Institut PPRIME, CNRS-Université de Poitiers-ENSMA, Poitiers, France
André V. G. Cavalieri
Affiliation:
Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, 12228-900 São José dos Campos, SP, Brazil
Aaron Towne
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA
Sanjiva K. Lele
Affiliation:
Department of Mechanical Engineering and Department of Aeronautics & Astronautics, Stanford University, Stanford, CA 94305, USA
Tim Colonius
Affiliation:
Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA 91125, USA
Oliver T. Schmidt
Affiliation:
Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: gbres@cascadetechnologies.com
Get access Rights & Permissions [Opens in a new window]

Abstract

To investigate the effects of the nozzle-exit conditions on jet flow and sound fields, large-eddy simulations of an isothermal Mach 0.9 jet issued from a convergent-straight nozzle are performed at a diameter-based Reynolds number of 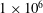$1\times 10^{6}$. The simulations feature near-wall adaptive mesh refinement, synthetic turbulence and wall modelling inside the nozzle. This leads to fully turbulent nozzle-exit boundary layers and results in significant improvements for the flow field and sound predictions compared with those obtained from the typical approach based on laminar flow in the nozzle. The far-field pressure spectra for the turbulent jet match companion experimental measurements, which use a boundary-layer trip to ensure a turbulent nozzle-exit boundary layer to within 0.5 dB for all relevant angles and frequencies. By contrast, the initially laminar jet results in greater high-frequency noise. For both initially laminar and turbulent jets, decomposition of the radiated noise into azimuthal Fourier modes is performed, and the results show similar azimuthal characteristics for the two jets. The axisymmetric mode is the dominant source of sound at the peak radiation angles and frequencies. The first three azimuthal modes recover more than 97 % of the total acoustic energy at these angles and more than 65 % (i.e. error less than 2 dB) for all angles. For the main azimuthal modes, linear stability analysis of the near-nozzle mean-velocity profiles is conducted in both jets. The analysis suggests that the differences in radiated noise between the initially laminar and turbulent jets are related to the differences in growth rate of the Kelvin–Helmholtz mode in the near-nozzle region.

JFM classification

Acoustics: Aeroacoustics Acoustics: Jet noise Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 83 - 124
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, N., Eriksson, L. E. & Davidson, L.2005 Effects of inflow conditions and subgrid model on LES for turbulent jets. AIAA Paper 2005-2925.Google Scholar
Bodart, J. & Larsson, J. 2011 Wall-modeled large eddy simulation in complex geometries with application to high-lift devices. In Annual Research Briefs, Center for Turbulence Research, Stanford University.Google Scholar
Bodony, D. J. & Lele, S. K. 2005 On using large-eddy simulation for the prediction of noise from cold and heated turbulent jets. Phys. Fluids 17 (8), 085103.Google Scholar
Bodony, D. J. & Lele, S. K. 2008 Current status of jet noise predictions using large-eddy simulation. AIAA J. 46, 346–380.Google Scholar
Bogey, C. & Bailly, C. 2005 Effects of inflow conditions and forcing on subsonic jet flows and noise. AIAA J. 43 (5), 1000–1007.Google Scholar
Bogey, C. & Bailly, C. 2010 Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 663, 507–538.Google Scholar
Bogey, C., Barré, S. & Bailly, C. 2008 Direct computation of the noise generated by subsonic jets originating from a straight pipe nozzle. Intl J. Aeroacoust. 7 (1), 1–21.Google Scholar
Bogey, C. & Marsden, O. 2016 Simulations of initially highly disturbed jets with experiment-like exit boundary layers. AIAA J. 54, 1299–1312.Google Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011 Large-eddy simulation of the flow and acoustic fields of a Reynolds number 105 subsonic jet with tripped exit boundary layers. Phys. Fluids 23 (3), 035104.Google Scholar
Bogey, C., Marsden, O. & Bailly, C. 2012 Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 105 . J. Fluid Mech. 701, 352–385.Google Scholar
Bradshaw, P., Ferriss, D. H. & Johnson, R. F. 1964 Turbulence in the noise-producing region of a circular jet. J. Fluid Mech. 19, 591–624.Google Scholar
Brès, G. A., Bose, S. T., Ham, F. E. & Lele, S. K.2014 Unstructured large eddy simulations for nozzle interior flow modeling and jet noise predictions. AIAA Paper 2014-2601.Google Scholar
Brès, G. A., Ham, F. E., Nichols, J. W. & Lele, S. K.2013 Nozzle wall modeling in unstructured large eddy simulations for hot supersonic jet predictions. AIAA Paper 2013-2142.Google Scholar
Brès, G. A., Ham, F. E., Nichols, J. W. & Lele, S. K. 2017 Unstructured large eddy simulations of supersonic jets. AIAA J. 55 (4), 1164–1184.Google Scholar
Brès, G. A., Jaunet, V., Le Rallic, M., Jordan, P., Colonius, T. & Lele, S. K.2015 Large eddy simulation for jet noise: the importance of getting the boundary layer right. AIAA Paper 2015-2535.Google Scholar
Brès, G. A., Jaunet, V., Le Rallic, M., Jordan, P., Towne, A., Schmidt, O. T., Colonius, T., Cavalieri, A. V. G. & Lele, S. K.2016 Large eddy simulation for jet noise: azimuthal decomposition and intermittency of the radiated sound. AIAA Paper 2016-3050.Google Scholar
Bridges, J. E. & Hussain, A. K. M. F. 1987 Roles of initial conditions and vortex pairing in jet noise. J. Sound Vib. 117 (2), 289–331.Google Scholar
Brown, C. & Bridges, J.2006 Small hot jet acoustic rig validation. Tech. Rep. TM 2006-214234. NASA.Google Scholar
Bühler, S., Kleiser, L. & Bogey, C. 2014a Simulation of subsonic turbulent nozzle jet flow and its near-field sound. AIAA J. 52 (8), 1653–1669.Google Scholar
Bühler, S., Obrist, D. & Kleiser, L. 2014b Laminar and turbulent nozzle-jet flows and their acoustic near-field. Phys. Fluids 26 (8), 086103.Google Scholar
Cavalieri, A. V. G., Daviller, G., Comte, P., Jordan, P., Tadmor, G. & Gervais, Y. 2011 Using large eddy simulation to explore sound-source mechanism in jets. J. Sound Vib. 330, 4098–4113.Google Scholar
Cavalieri, A. V. G., Jordan, P., Colonius, T. & Gervais, Y. 2012 Axisymmetric superdirectivity in subsonic jets. J. Fluid Mech. 704, 388–420.Google Scholar
Cavalieri, A. V. G., Rodríguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2013 Wavepackets in the velocity field of turbulent jets. J. Fluid Mech. 730, 559–592.Google Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24 (1), 011702.Google Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 88 (2), 397–413.Google Scholar
Ffowcs Williams, J. E. & Hawkings, D. L. 1969 Sound generation by turbulence and surfaces in arbitrary motion. Phil. Trans. R. Soc. Lond. A 264, 321–342.Google Scholar
Fontaine, R. A., Elliot, G. S., Austin, J. M. & Freund, J. B. 2015 Very near-nozzle shear-layer turbulence and jet noise. J. Fluid Mech. 770, 27–51.Google Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound. AIAA J. 35 (4), 740–742.Google Scholar
Freund, J. B. 2001 Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 438, 277–305.Google Scholar
Gottlieb, S. & Shu, W. 1998 Math. Comput. 67 (221), 73–85.Google Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Hill, G., Jenkins, R. C. & Gilbert, B. L. 1976 Effects of the initial boundary-layer state on turbulent jet mixing. AIAA J. 14 (11), 1513–1514.Google Scholar
Husain, Z. D. & Hussain, A. K. M. F. 1979 Axisymmetric mixing layer: influence of the initial and boundary conditions. AIAA J. 17 (1), 48–55.Google Scholar
Hussain, A. K. M. F. & Zedan, M. F. 1978a Effects of the initial condition on the axisymmetric free shear layer: effects of the initial fluctuation level. Phys. Fluids 21 (9), 1475–1481.Google Scholar
Hussain, A. K. M. F. & Zedan, M. F. 1978b Effects of the initial condition on the axisymmetric free shear layer: effects of the initial momentum thickness. Phys. Fluids 21 (7), 1100–1112.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.Google Scholar
Juvé, D., Sunyach, M. & Comte-Bellot, G. 1979 Filtered azimuthal correlations in the acoustic far field of a subsonic jet. AIAA J. 17 (1), 112–113.Google Scholar
Karon, A. Z. & Ahuja, K. K.2013 Effect of nozzle-exit boundary layer on jet noise. AIAA Paper 2013-0615.Google Scholar
Kawai, S. & Larsson, J. 2012 Wall-modeling in large eddy simulation: length scales, grid resolution, and accuracy. Phys. Fluids 24 (1), 015105.Google Scholar
Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186 (2), 652–665.Google Scholar
Kopiev, V., Chernyshev, S., Faranosov, G., Zaitsev, M. & Belayev, I.2010 Correlations of jet noise azimuthal components and their role in source identification. AIAA Paper 2010-4018.Google Scholar
Larsson, J., Kawai, S., Bodart, J. & Bermejo-Moreno, I. 2016 Large eddy simulation with modeled wall-stress: recent progress and future directions. JSME Mech. Engng Rev. 3 (1), 15–00418.Google Scholar
Lesshafft, L. & Huerre, P. 2007 Linear impulse response in hot round jets. Phys. Fluids 19 (2), 024102.Google Scholar
Lockard, D. P. 2000 An efficient, two-dimensional implementation of the Ffowcs Williams and Hawkings equation. J. Sound Vib. 229, 897–911.Google Scholar
Lorteau, M., Cléro, F. & Vuillot, F. 2015 Analysis of noise radiation mechanisms in a hot subsonic jet from a validated large eddy simulation solution. Phys. Fluids 27 (7), 075108.Google Scholar
Mani, A. 2012 Analysis and optimization of numerical sponge layers as a nonreflective boundary treatment. J. Comput. Phys. 231, 704–7016.Google Scholar
Mendez, S., Shoeybi, M., Sharma, A., Ham, F. E., Lele, S. K. & Moin, P. 2012 Large-eddy simulations of perfectly expanded supersonic jets using an unstructured solver. AIAA J. 50 (5), 1103–1118.Google Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.Google Scholar
Michalke, A. & Fuchs, H. V. 1975 On turbulence and noise of an axisymmetric shear flow. J. Fluid Mech. 70, 179–205.Google Scholar
Morris, P. J., Long, L. N., Scheidegger, T. E. & Boluriaan, S. 2002 Simulations of supersonic jet noise. Intl J. Aeroacoust. 1 (1), 17–41.Google Scholar
Petersen, R. A. & Samet, M. M. 1988 On the preferred mode of jet instability. J. Fluid Mech. 194 (1), 153–173.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374.Google Scholar
Pouangué, A. F., Sanjosé, M. & Moreau, S.2012 Jet noise simulation with realistic nozzle geometries using fully unstructured LES solver. AIAA Paper 2012-2190.Google Scholar
Sandberg, R. D., Sandham, N. D. & Suponitsky, V. 2012 DNS of a compressible pipe flow exiting into a coflow. Intl J. Heat Fluid Flow 35, 33–44.Google Scholar
Sasaki, K., Cavalieri, A. V. G., Jordan, P., Schmidt, O. T., Colonius, T. & Brès, G. A. 2017 High-frequency wavepackets in turbulent jets. J. Fluid Mech. 830, R2.Google Scholar
Scarano, F. 2002 Iterative image deformation methods in PIV. Meas. Sci. Tech. 13 (1), R1–R19.Google Scholar
Schlichting, H. & Gertsen, K. 2000 Boundary Layer Theory, 8th edn. Springer.Google Scholar
Schmidt, O. T., Towne, A., Colonius, T., Cavalieri, A. V. G., Jordan, P. & Brès, G. A. 2017 Wavepackets and trapped acoustic modes in a turbulent jet: coherent structure eduction and global stability. J. Fluid Mech. 825, 1153–1181.Google Scholar
Shur, M. L., Spalart, P. R. & Strelets, M. K. 2005a Noise prediction for increasingly complex jets. Part I. Methods and tests. Intl J. Aeroacoust. 4 (3–4), 213–246.Google Scholar
Shur, M. L., Spalart, P. R. & Strelets, M. K. 2005b Noise prediction for increasingly complex jets. Part II. Applications. Intl J. Aeroacoust. 4 (3–4), 247–266.Google Scholar
Shur, M. L., Spalart, P. R. & Strelets, M. K. 2011 Noise prediction for underexpanded jets in static and flight conditions. AIAA J. 49 (9), 2000–2017.Google Scholar
Spalart, P. R. 2009 Detached-eddy simulation. Annu. Rev. Fluid Mech. 41, 181–202.Google Scholar
Suponitsky, V., Sandham, N. D. & Morfey, C. L. 2010 Linear and nonlinear mechanisms of sound radiation by instability waves in subsonic jet. J. Fluid Mech. 658, 509–538.Google Scholar
Suzuki, T. & Colonius, T. 2006 Instability waves in a subsonic round jet detected using a near-field phased microphone array. J. Fluid Mech. 565, 197–226.Google Scholar
Towne, A., Cavalieri, A. V. G., Jordan, P., Colonius, T., Schmidt, O., Jaunet, V. & Brès, G. A. 2017 Acoustic resonance in the potential core of subsonic jets. J. Fluid Mech. 825, 1113–1152.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. Society for Industrial Mathematics.Google Scholar
Uzun, A. & Hussaini, Y. M. 2007 Investigation of high frequency noise generation in the near-nozzle region of a jet using large eddy simulation. J. Theor. Comput. Fluid Dyn. 21 (4), 291–321.Google Scholar
Uzun, A., Lyrintsis, A. S. & Blaisdell, G. A. 2004 Coupling of integral acoustics methods with LES for jet noise prediction. Intl J. Aeroacoust. 3 (4), 297–346.Google Scholar
Vreman, A. 2004 An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys. Fluids 16 (10), 3670–3681.Google Scholar
Vuillot, F., Lupoglazoff, N., Lorteau, M. & Cléro, F.2016 Large eddy simulation of jet noise from unstructured grids with turbulent nozzle boundary layer. AIAA Paper 2016-3046.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.Google Scholar
Wieneke, B. 2005 Stereo-PIV using self-calibration on particle images. Exp. Fluids 39, 267–280.Google Scholar
Zaman, K. B. M. Q. 1985 Effect of initial condition on subsonic jet noise. AIAA J. 23 (9), 1370–1373.Google Scholar
Zaman, K. B. M. Q. 1998 Asymptotic spreading rates of initially compressible jets: experiment and analysis. Phys. Fluids 10 (10), 2652–2660.Google Scholar
Zaman, K. B. M. Q. 1999 Spreading characteristics of compressible jets from nozzles of various geometries. J. Fluid Mech. 383, 197–228.Google Scholar
Zaman, K. B. M. Q. 2012 Effect of initial boundary-layer state on subsonic jet noise. AIAA J. 50 (8), 1784–1795.Google Scholar

Brès et al. supplementary movie 1

Animation of the instantaneous pressure fluctuations (grey scale) and temperature field (color scale) for the case BL69M_WM_Turb in the mid-section of the jet plume (left image), at the cross-section x/D = 20 (right image), and in the potential core (left insert). The nozzle external surface is shown in metallic grey and the white dashed circle in the right image represents the outline of the nozzle lip. The vertical white dashed line in the left image indicated the location of the cross-section x/D = 20 and its dimension are y/D = -6 to 6 (i.e., limit of extracted LES database)

Download Brès et al. supplementary movie 1(Video)
Video 23.4 MB
Supplementary material: File

Brès et al. supplementary material

Nozzle profile, flow and acoustics data from experiment and simulation

Download Brès et al. supplementary material(File)
File 222.5 KB