Published online by Cambridge University Press: 28 November 2017
Experiments on the inertial flow transitions of a particle–fluid suspension in the concentric cylinder (Taylor–Couette) flow with rotating inner cylinder and stationary outer cylinder are reported. The radius ratio of the apparatus was
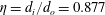 $\unicode[STIX]{x1D702}=d_{i}/d_{o}=0.877$
, where
$\unicode[STIX]{x1D702}=d_{i}/d_{o}=0.877$
, where
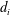 $d_{i}$
and
$d_{i}$
and
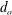 $d_{o}$
are the diameters of inner and outer cylinders. The ratio of the axial length to the radial gap of the annulus
$d_{o}$
are the diameters of inner and outer cylinders. The ratio of the axial length to the radial gap of the annulus
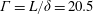 $\unicode[STIX]{x1D6E4}=L/\unicode[STIX]{x1D6FF}=20.5$
, where
$\unicode[STIX]{x1D6E4}=L/\unicode[STIX]{x1D6FF}=20.5$
, where
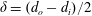 $\unicode[STIX]{x1D6FF}=(d_{o}-d_{i})/2$
. The suspensions are formed of non-Brownian particles of equal density to the suspending fluid, of two sizes such that the ratio of annular gap to the mean particle diameter
$\unicode[STIX]{x1D6FF}=(d_{o}-d_{i})/2$
. The suspensions are formed of non-Brownian particles of equal density to the suspending fluid, of two sizes such that the ratio of annular gap to the mean particle diameter
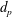 $d_{p}$
was either
$d_{p}$
was either
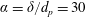 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}/d_{p}=30$
or
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}/d_{p}=30$
or
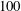 $100$
. For the experiments with
$100$
. For the experiments with
 $\unicode[STIX]{x1D6FC}=100$
, the particle volume fraction was
$\unicode[STIX]{x1D6FC}=100$
, the particle volume fraction was
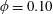 $\unicode[STIX]{x1D719}=0.10$
and for the experiments with
$\unicode[STIX]{x1D719}=0.10$
and for the experiments with
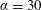 $\unicode[STIX]{x1D6FC}=30$
,
$\unicode[STIX]{x1D6FC}=30$
,
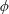 $\unicode[STIX]{x1D719}$
was varied over
$\unicode[STIX]{x1D719}$
was varied over
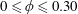 $0\leqslant \unicode[STIX]{x1D719}\leqslant 0.30$
. The focus of the work is on determining the influence of particle loading and size on inertial flow transitions. The primary effects of the particles were a reduction of the maximum Reynolds number for the circular Couette flow (CCF) and several non-axisymmetric flow states not seen for a pure fluid with only inner cylinder rotation; here the Reynolds number is
$0\leqslant \unicode[STIX]{x1D719}\leqslant 0.30$
. The focus of the work is on determining the influence of particle loading and size on inertial flow transitions. The primary effects of the particles were a reduction of the maximum Reynolds number for the circular Couette flow (CCF) and several non-axisymmetric flow states not seen for a pure fluid with only inner cylinder rotation; here the Reynolds number is
 $Re=\unicode[STIX]{x1D6FF}d_{i}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D70C}/2\unicode[STIX]{x1D707}_{s}$
, where
$Re=\unicode[STIX]{x1D6FF}d_{i}\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D70C}/2\unicode[STIX]{x1D707}_{s}$
, where
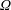 $\unicode[STIX]{x1D6FA}$
is the rotation rate of the inner cylinder and
$\unicode[STIX]{x1D6FA}$
is the rotation rate of the inner cylinder and
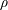 $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
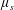 $\unicode[STIX]{x1D707}_{s}$
are the density and effective viscosity of the suspension. For purposes of maintaining uniform particle distribution, the rotation rate of the inner cylinder (or
$\unicode[STIX]{x1D707}_{s}$
are the density and effective viscosity of the suspension. For purposes of maintaining uniform particle distribution, the rotation rate of the inner cylinder (or
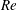 $Re$
) was decreased slowly from a state other than CCF to probe the transitions. When
$Re$
) was decreased slowly from a state other than CCF to probe the transitions. When
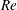 $Re$
was decreased, pure fluid transitions from wavy Taylor vortex flow (WTV) to Taylor vortex flow (TVF) to CCF occurred. The suspension transitions differed. For
$Re$
was decreased, pure fluid transitions from wavy Taylor vortex flow (WTV) to Taylor vortex flow (TVF) to CCF occurred. The suspension transitions differed. For
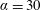 $\unicode[STIX]{x1D6FC}=30$
and
$\unicode[STIX]{x1D6FC}=30$
and
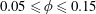 $0.05\leqslant \unicode[STIX]{x1D719}\leqslant 0.15$
, with reduction of
$0.05\leqslant \unicode[STIX]{x1D719}\leqslant 0.15$
, with reduction of
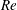 $Re$
, additional non-axisymmetric flow states, namely spiral vortex flow (SVF) and ribbons (RIB), were observed between TVF and CCF. At
$Re$
, additional non-axisymmetric flow states, namely spiral vortex flow (SVF) and ribbons (RIB), were observed between TVF and CCF. At
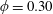 $\unicode[STIX]{x1D719}=0.30$
, the flow transitions observed were only non-axisymmetric: from wavy spiral vortices (WSV) to SVF to CCF. The values of
$\unicode[STIX]{x1D719}=0.30$
, the flow transitions observed were only non-axisymmetric: from wavy spiral vortices (WSV) to SVF to CCF. The values of
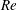 $Re$
corresponding to each flow transition were observed to reduce with increase in particle loading for
$Re$
corresponding to each flow transition were observed to reduce with increase in particle loading for
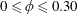 $0\leqslant \unicode[STIX]{x1D719}\leqslant 0.30$
, with the initial transition away from CCF, for example, occurring at
$0\leqslant \unicode[STIX]{x1D719}\leqslant 0.30$
, with the initial transition away from CCF, for example, occurring at
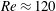 $Re\approx 120$
for the pure fluid and
$Re\approx 120$
for the pure fluid and
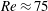 $Re\approx 75$
for the
$Re\approx 75$
for the
 $\unicode[STIX]{x1D719}=0.30$
suspension. When the particle size was reduced to yield
$\unicode[STIX]{x1D719}=0.30$
suspension. When the particle size was reduced to yield
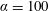 $\unicode[STIX]{x1D6FC}=100$
, at
$\unicode[STIX]{x1D6FC}=100$
, at
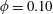 $\unicode[STIX]{x1D719}=0.10$
, only the RIB (and no SVF) was observed between TVF and CCF.
$\unicode[STIX]{x1D719}=0.10$
, only the RIB (and no SVF) was observed between TVF and CCF.