Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T20:39:38.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Isotropically active colloids under uniform force fields: from forced to spontaneous motion

Published online by Cambridge University Press:  14 April 2021

Saikat Saha Open the ORCID record for Saikat Saha [Opens in a new window] ,
Ehud Yariv Open the ORCID record for Ehud Yariv [Opens in a new window]  and
Ory Schnitzer Open the ORCID record for Ory Schnitzer [Opens in a new window]
Saikat Saha
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa32000, Israel
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa32000, Israel
Ory Schnitzer
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK
*
†Email address for correspondence: udi@technion.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the inertia-free motion of an isotropic chemically active particle which is exposed to a weak uniform force field. This problem is characterised by two velocity scales, a ‘chemical’ scale associated with diffusio-osmosis and a ‘mechanical’ scale associated with the external force. The motion animated by the force deforms the originally spherically symmetric solute cloud surrounding the particle, thus resulting in a concomitant diffusio-osmotic flow which, in turn, modifies the particle speed. A weak-force linearisation furnishes a closed-form expression for the particle velocity as a function of the intrinsic Péclet number $\alpha$ associated with the chemical velocity scale. 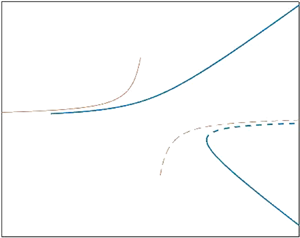We find that the predicted velocity may become singular at $\alpha =4$, and that this happens under the same conditions on the surface parameters for which the associated unforced problem is known to exhibit, for $\alpha >4$, a symmetry-breaking instability giving rise to steady spontaneous motion (Michelin, Lauga & Bartolo, Phys. Fluids, vol. 25, 2013, 061701). Here, a local analysis in a distinguished region near $\alpha =4$, wherein the velocity scaling is amplified, yields a closed-form description of the imperfect bifurcation which bridges between a perturbed stationary state and a perturbed spontaneous motion. Remarkably, while the direction of spontaneous motion in the absence of an external force is random, in the perturbed case that motion is rendered steady solely in the directions parallel or antiparallel to the external force.

JFM classification

Complex Fluids: Active matter Mass Transport: Coupled diffusion and flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 916 , 10 June 2021 , A47
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Acrivos, A. & Taylor, T.D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5 (4), 387–394.CrossRefGoogle Scholar
Anderson, J.L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 30, 139–165.CrossRefGoogle Scholar
Batchelor, G.K. 1979 Mass transfer from a particle suspended in fluid with a steady linear ambient velocity distribution. J. Fluid Mech. 95 (02), 369–400.CrossRefGoogle Scholar
Boniface, D., Cottin-Bizonne, C., Kervil, R., Ybert, C. & Detcheverry, F. 2019 Self-propulsion of symmetric chemically active particles: point-source model and experiments on camphor disks. Phys. Rev. E 99 (6), 062605.CrossRefGoogle ScholarPubMed
Frankel, N.A. & Acrivos, A. 1968 Heat and mass transfer from small spheres and cylinders freely suspended in shear flow. Phys. Fluids 11, 1913–1918.CrossRefGoogle Scholar
Golestanian, R., Liverpool, T.B. & Ajdari, A. 2007 Designing phoretic micro-and nano-swimmers. New J. Phys. 9, 126.CrossRefGoogle Scholar
Hinch, E.J. 1991 Perturbation Methods. Cambridge University Press.CrossRefGoogle Scholar
Hu, W.-F., Lin, T.-S., Rafai, S. & Misbah, C. 2019 Chaotic swimming of phoretic particles. Phys. Rev. Lett. 123 (23), 238004.CrossRefGoogle ScholarPubMed
Izri, Z., Van Der Linden, M.N., Michelin, S. & Dauchot, O. 2014 Self-propulsion of pure water droplets by spontaneous Marangoni-stress-driven motion. Phys. Rev. Lett. 113 (24), 248302.CrossRefGoogle ScholarPubMed
Kim, S. & Karrila, S.J. 2005 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Lippera, K., Benzaquen, M. & Michelin, S. 2020 a Alignment and scattering of colliding active droplets. Soft Matter. 17 (2), 365–375.CrossRefGoogle Scholar
Lippera, K., Benzaquen, M. & Michelin, S. 2020 b Bouncing, chasing, or pausing: asymmetric collisions of active droplets. Phys. Rev. Fluids 5 (3), 032201.CrossRefGoogle Scholar
Lippera, K., Morozov, M., Benzaquen, M. & Michelin, S. 2020 c Collisions and rebounds of chemically active droplets. J. Fluid Mech. 886, A17.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2014 Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604.CrossRefGoogle Scholar
Michelin, S., Lauga, E. & Bartolo, D. 2013 Spontaneous autophoretic motion of isotropic particles. Phys. Fluids 25 (6), 061701.CrossRefGoogle Scholar
Paxton, W.F., Kistler, K.C., Olmeda, C.C., Sen, A., Angelo, S.K.S., Cao, Y., Mallouk, T.E., Lammert, P.E. & Crespi, V.H. 2004 Catalytic nanomotors: autonomous movement of striped nanorods. J. Am. Chem. Soc. 126 (41), 13424–13431.CrossRefGoogle ScholarPubMed
Rednikov, A.Y., Kurdyumov, V.N., Ryazantsev, Y.S. & Velarde, M.G. 1995 The role of time-varying gravity on the motion of a drop induced by marangoni instability. Phys. Fluids 7 (11), 2670–2678.CrossRefGoogle Scholar
Rednikov, A.Y., Ryazantsev, Y.S. & Velárde, M.G. 1994 a Active drops and drop motions due to nonequilibrium phenomena. J. Non-Equilib. Thermodyn. 19 (1), 95–113.CrossRefGoogle Scholar
Rednikov, A.Y., Ryazantsev, Y.S. & Velárde, M.G. 1994 b Drop motion with surfactant transfer in a homogeneous surrounding. Phys. Fluids 6 (2), 451–468.CrossRefGoogle Scholar
Rednikov, A.Y., Ryazantsev, Y.S. & Velárde, M.G. 1994 c Drop motion with surfactant transfer in an inhomogeneous medium. Intl J. Heat Mass Transfer 37, 361–374.CrossRefGoogle Scholar
Rednikov, A.Y., Ryazantsev, Y.S. & Velárde, M.G. 1994 d On the development of translational subcritical marangoni instability for a drop with uniform internal heat generation. J. Colloid Interface Sci. 164 (1), 168–180.CrossRefGoogle Scholar
Sondak, D., Hawley, C., Heng, S., Vinsonhaler, R., Lauga, E. & Thiffeault, J.-L. 2016 Can phoretic particles swim in two dimensions? Phys. Rev. E 94 (6), 062606.CrossRefGoogle ScholarPubMed
Velarde, M.G., Rednikov, A.Y. & Ryazantsev, Y.S. 1996 Drop motions and interfacial instability. J. Phys.: Condens. Matter 8 (47), 9233–9247.Google Scholar
Yariv, E. 2017 Two-dimensional phoretic swimmers: the singular weak-advection limits. J. Fluid Mech. 816, R3.CrossRefGoogle Scholar
Yariv, E. 2019 Mass transfer from a cylindrical body in a linear ambient velocity distribution. Phys. Rev. Fluids 4 (12), 124503.CrossRefGoogle Scholar
Yariv, E. & Crowdy, D. 2020 Phoretic self-propulsion of Janus disks in the fast-reaction limit. Phys. Rev. Fluids 5 (11), 112001.CrossRefGoogle Scholar
Yariv, E. & Kaynan, U. 2017 Phoretic drag reduction of chemically active homogeneous spheres under force fields and shear flows. Phys. Rev. Fluids 2 (1), 012201.CrossRefGoogle Scholar
Yariv, E. & Michelin, S. 2015 Phoretic self-propulsion at large Péclet numbers. J. Fluid Mech. 768, R1.CrossRefGoogle Scholar