Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T21:24:17.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian accelerations of particles in superfluid turbulence

Published online by Cambridge University Press:  07 February 2013

M. La Mantia ,
D. Duda ,
M. Rotter  and
L. Skrbek
M. La Mantia*
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague,Czech Republic
D. Duda
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague,Czech Republic
M. Rotter
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague,Czech Republic
L. Skrbek
Affiliation:
Faculty of Mathematics and Physics, Charles University, Ke Karlovu 3, 121 16 Prague,Czech Republic
*
†Email address for correspondence: lamantia@nbox.troja.mff.cuni.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

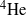Quantum turbulence in thermal counterflow of superfluid ${\text{} }^{4} \mathrm{He} $ is studied at length scales comparable to the mean distance 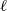$\ell $ between quantized vortices. The Lagrangian dynamics of solid deuterium particles, of radius 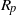${R}_{p} $ about one order of magnitude smaller than 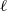$\ell $, is analysed in a planar section of the experimental volume by using the particle tracking velocimetry technique. We show that the average amplitude of the acceleration of the particles seems to increase as the temperature decreases and applied heat flux increases and this can be explained by exploiting the two-fluid model of superfluid 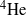${\text{} }^{4} \mathrm{He} $. We also report that, at the probed length scales, the normalized distribution of the acceleration of the particles appears to follow an unexpected classical-like behaviour.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Quantum fluids Vortex Flows: Vortex dynamics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , R9
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adachi, H. & Tsubota, M. 2011 Numerical study of velocity statistics in steady counterflow quantum turbulence. Phys. Rev. B 83, 132503.CrossRefGoogle Scholar
Baggaley, A. W. & Barenghi, C. F. 2011 Quantum turbulent velocity statistics and quasiclassical limit. Phys. Rev. E 84, 067301.CrossRefGoogle ScholarPubMed
Bewley, G. P., Lathrop, D. P. & Sreenivasan, K. R. 2006 Superfluid helium: visualization of quantized vortices. Nature 441, 588.CrossRefGoogle ScholarPubMed
Chagovets, T. V. & Van Sciver, S. W. 2011 A study of thermal counterflow using particle tracking velocimetry. Phys. Fluids 23, 107102.CrossRefGoogle Scholar
Guo, W., Cahn, S. B., Nikkel, J. A., Vinen, W. F. & McKinsey, D. N. 2010 Visualization study of counterflow in superfluid ${\text{} }^{4} \mathrm{He} $ using metastable helium molecules. Phys. Rev. Lett. 105, 045301.CrossRefGoogle Scholar
La Mantia, M., Chagovets, T. V., Rotter, M. & Skrbek, L. 2012 Testing the performance of a cryogenic visualization system on thermal counterflow by using hydrogen and deuterium solid tracers. Rev. Sci. Instrum. 83, 055109.CrossRefGoogle ScholarPubMed
La Porta, A., Voth, G. A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2001 Fluid particle accelerations in fully developed turbulence. Nature 409, 1017–1019.CrossRefGoogle ScholarPubMed
Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004a Experimental Lagrangian acceleration probability density function measurement. Physica D 193, 245–251.CrossRefGoogle Scholar
Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004b Three-dimensional structure of the Lagrangian acceleration in turbulent flows. Phys. Rev. Lett. 93, 214501.CrossRefGoogle ScholarPubMed
Mordant, N., Metz, P., Michel, O. & Pinton, J.-F. 2001 Measurement of Lagrangian velocity in fully developed turbulence. Phys. Rev. Lett. 87, 214501.CrossRefGoogle ScholarPubMed
Paoletti, M. S., Fisher, M. E., Sreenivasan, K. R. & Lathrop, D. P. 2008 Velocity statistics distinguish quantum turbulence from classical turbulence. Phys. Rev. Lett. 101, 154501.CrossRefGoogle ScholarPubMed
Poole, D. R., Barenghi, C. F., Sergeev, Y. A. & Vinen, W. F. 2005 Motion of tracer particles in He II. Phys. Rev. B 71, 064514.CrossRefGoogle Scholar
Qureshi, N. M., Arrieta, U., Baudet, C., Cartellier, A., Gagne, Y. & Bourgoin, M. 2008 Acceleration statistics of inertial particles in turbulent flow. Eur. Phys. J. B 66, 531–536.CrossRefGoogle Scholar
Qureshi, N. M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99, 184502.CrossRefGoogle ScholarPubMed
Sbalzarini, I. F. & Koumoutsakos, P. 2005 Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 151, 182–195.CrossRefGoogle ScholarPubMed
Sergeev, Y. A. & Barenghi, C. F. 2009 Particles-vortex interactions and flow visualization in ${\text{} }^{4} \mathrm{He} $ . J. Low Temp. Phys. 157, 429–475.CrossRefGoogle Scholar
Sergeev, Y. A., Wang, S., Meneguz, E. & Barenghi, C. F. 2007 Influence of normal fluid disturbances on interactions of solid particles with quantized vortices. J. Low Temp. Phys. 146, 417–434.CrossRefGoogle Scholar
Skrbek, L. & Sreenivasan, K. R. 2012 Developed quantum turbulence and its decay. Phys. Fluids 24, 011301.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar
Van Sciver, S. W. & Barenghi, C. F. 2010 Visualisation of quantum turbulence. In Progress in Low Temperature Physics: Quantum Turbulence (ed. Tsubota, M. & Halperin, W. P.), pp. 247–303. Springer.Google Scholar
Vinen, W. F. & Niemela, J. J. 2002 Quantum turbulence. J. Low Temp. Phys. 128, 167–231.CrossRefGoogle Scholar
Voth, G. A., La Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.CrossRefGoogle Scholar
White, A. C., Barenghi, C. F., Proukakis, N. P., Youd, A. J. & Wacks, D. H. 2010 Nonclassical velocity statistics in a turbulent atomic Bose–Einstein condensate. Phys. Rev. Lett. 104, 075301.CrossRefGoogle Scholar
Zhang, T. & Van Sciver, S. W. 2005 Large-scale turbulent flow around a cylinder in counterflow superfluid ${\text{} }^{4} \mathrm{He} $ (He(II)). Nat. Phys. 1, 36–38.CrossRefGoogle Scholar