Published online by Cambridge University Press: 01 October 2019
Annular Couette flow is the flow between two coaxial cylinders driven by the axial translation of the inner cylinder. It is investigated using direct numerical simulation in long domains, with an emphasis on the laminar–turbulent coexistence regime found for marginally low values of the Reynolds number. Three distinct flow regimes are demonstrated as the radius ratio 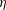 $\unicode[STIX]{x1D702}$ is decreased from 0.8 to 0.5 and finally to 0.1. The high-
$\unicode[STIX]{x1D702}$ is decreased from 0.8 to 0.5 and finally to 0.1. The high-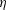 $\unicode[STIX]{x1D702}$ regime features helically shaped turbulent patches coexisting with laminar flow, as in planar shear flows. The moderate-
$\unicode[STIX]{x1D702}$ regime features helically shaped turbulent patches coexisting with laminar flow, as in planar shear flows. The moderate-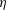 $\unicode[STIX]{x1D702}$ regime does not feature any marked laminar–turbulent coexistence. In an effort to discard confinement effects, proper patterning is, however, recovered by artificially extending the azimuthal span beyond
$\unicode[STIX]{x1D702}$ regime does not feature any marked laminar–turbulent coexistence. In an effort to discard confinement effects, proper patterning is, however, recovered by artificially extending the azimuthal span beyond 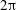 $2\unicode[STIX]{x03C0}$. Eventually, the low-
$2\unicode[STIX]{x03C0}$. Eventually, the low-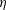 $\unicode[STIX]{x1D702}$ regime features localised turbulent structures different from the puffs commonly encountered in transitional pipe flow. In this new coexistence regime, turbulent fluctuations are surprisingly short-ranged. Implications are discussed in terms of phase transition and critical scaling.
$\unicode[STIX]{x1D702}$ regime features localised turbulent structures different from the puffs commonly encountered in transitional pipe flow. In this new coexistence regime, turbulent fluctuations are surprisingly short-ranged. Implications are discussed in terms of phase transition and critical scaling.
Present address: Japan Aerospace Exploration Agency, Tokyo 182-8522, Japan.
Time evolution of fluctuating velocity fields viewed at mid-gap (top) and on a cross section (bottom three panels), for η = 0.1, Lθ= 16π, and Re = 275, where the new flow regime has been observed. From top to bottom, contours show x-z (or x-θ) distribution of ur', and r-θ views of the streamwise ux', radial ur', and azimuthal components uθ', at the same time. The time span visualized here is 800 time units (h/uw).