Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T16:55:05.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale-vortex dynamos in planar rotating convection

Published online by Cambridge University Press:  20 February 2017

Céline Guervilly Open the ORCID record for Céline Guervilly [Opens in a new window] ,
David W. Hughes  and
Chris A. Jones
Céline Guervilly
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
David W. Hughes
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
Chris A. Jones
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

Several recent studies have demonstrated how large-scale vortices may arise spontaneously in rotating planar convection. Here, we examine the dynamo properties of such flows in rotating Boussinesq convection. For moderate values of the magnetic Reynolds number (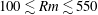$100\lesssim Rm\lesssim 550$, with 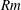$Rm$ based on the box depth and the convective velocity), a large-scale (i.e. system-size) magnetic field is generated. The amplitude of the magnetic energy oscillates in time, nearly out of phase with the oscillating amplitude of the large-scale vortex. The large-scale vortex is disrupted once the magnetic field reaches a critical strength, showing that these oscillations are of magnetic origin. The dynamo mechanism relies on those components of the flow that have length scales lying between that of the large-scale vortex and the typical convective cell size; smaller-scale flows are not required. The large-scale vortex plays a crucial role in the magnetic induction despite being essentially two-dimensional; we thus refer to this dynamo as a large-scale-vortex dynamo. For larger magnetic Reynolds numbers, the dynamo is small scale, with a magnetic energy spectrum that peaks at the scale of the convective cells. In this case, the small-scale magnetic field continuously suppresses the large-scale vortex by disrupting the correlations between the convective velocities that allow it to form. The suppression of the large-scale vortex at high 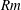$Rm$ therefore probably limits the relevance of the large-scale-vortex dynamo to astrophysical objects with moderate values of 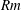$Rm$, such as planets. In this context, the ability of the large-scale-vortex dynamo to operate at low magnetic Prandtl numbers is of great interest.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 333 - 360
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubert, J. 2005 Steady zonal flows in spherical shell dynamos. J. Fluid Mech. 542, 53–67.CrossRefGoogle Scholar
Bakas, N. A. & Ioannou, P. J. 2014 A theory for the emergence of coherent structures in beta-plane turbulence. J. Fluid Mech. 740, 312–341.Google Scholar
Calkins, M. A., Julien, K., Tobias, S. M., Aurnou, J. M. & Marti, P. 2016 Convection-driven kinematic dynamos at low Rossby and magnetic Prandtl numbers: single mode solutions. Phys. Rev. E 93 (2), 023115.Google ScholarPubMed
Cattaneo, F., Emonet, T. & Weiss, N. O. 2003 On the interaction between convection and magnetic fields. Astrophys. J. 588, 1183–1198.Google Scholar
Cattaneo, F. & Hughes, D. W. 2006 Dynamo action in a rotating convective layer. J. Fluid Mech. 553, 401–418.Google Scholar
Chan, K. L. 2007 Rotating convection in f-boxes: faster rotation. Astron. Nachr. 328, 1059–1061.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Childress, S. & Soward, A. M. 1972 Convection-driven hydromagnetic dynamo. Phys. Rev. Lett. 29, 837–839.CrossRefGoogle Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166, 97–114.Google Scholar
Constantinou, N. C., Farrell, B. F. & Ioannou, P. J. 2016 Statistical state dynamics of jet/wave coexistence in barotropic beta-plane turbulence. J. Atmos. Sci. 73 (5), 2229–2253.Google Scholar
Courvoisier, A., Hughes, D. W. & Tobias, S. M. 2009 Mean induction and diffusion: the influence of spatial coherence. J. Fluid Mech. 627, 403–421.Google Scholar
Favier, B. & Proctor, M. R. E. 2013 Kinematic dynamo action in square and hexagonal patterns. Phys. Rev. E 88 (5), 053011.Google ScholarPubMed
Favier, B., Silvers, L. J. & Proctor, M. R. E. 2014 Inverse cascade and symmetry breaking in rapidly-rotating Boussinesq convection. Phys. Fluids 26 (9), 096605.Google Scholar
Galperin, B., Sukoriansky, S. & Dikovskaya, N. 2010 Geophysical flows with anisotropic turbulence and dispersive waves: flows with a 𝛽-effect. Ocean Dyn. 60, 427–441.Google Scholar
Gastine, T. & Wicht, J. 2012 Effects of compressibility on driving zonal flow in gas giants. Icarus 219, 428–442.Google Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2014 Large-scale vortices in rapidly rotating Rayleigh-Bénard convection. J. Fluid Mech. 758, 407–435.CrossRefGoogle Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2015 Generation of magnetic fields by large-scale vortices in rotating convection. Phys. Rev. E 91 (4), 041001.Google Scholar
Heimpel, M., Aurnou, J. & Wicht, J. 2005 Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 438, 193–196.Google Scholar
Hori, K., Wicht, J. & Christensen, U. R. 2010 The effect of thermal boundary conditions on dynamos driven by internal heating. Phys. Earth Planet. Inter. 182, 85–97.Google Scholar
Hughes, D. W. & Cattaneo, F. 2008 The alpha-effect in rotating convection: size matters. J. Fluid Mech. 594, 445–461.Google Scholar
Hughes, D. W. & Cattaneo, F. 2016 Strong-field dynamo action in rapidly rotating convection with no inertia. Phys. Rev. E 93 (6), 061101.Google Scholar
Hughes, D. W. & Proctor, M. R. E. 2013 The effect of velocity shear on dynamo action due to rotating convection. J. Fluid Mech. 717, 395–416.Google Scholar
Jones, C. A. 2000 Convection-driven geodynamo models. Phil. Trans. R. Soc. Lond. A 358, 873–897.CrossRefGoogle Scholar
Käpylä, P. J., Mantere, M. J. & Hackman, T. 2011 Starspots due to large-scale vortices in rotating turbulent convection. Astrophys. J. 742, 34–41.Google Scholar
Olson, P., Christensen, U. & Glatzmaier, G. A. 1999 Numerical modeling of the geodynamo: mechanisms of field generation and equilibration. J. Geophys. Res. 104, 10383–10404.Google Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112, 144501.Google Scholar
Soderlund, K. M., King, E. M. & Aurnou, J. M. 2012 The influence of magnetic fields in planetary dynamo models. Earth Planet. Sci. Lett. 333, 9–20.CrossRefGoogle Scholar
Soward, A. M. 1974 A convection-driven dynamo: I. The weak field case. Phil. Trans. R. Soc. Lond. A 275 (1256), 611–646.Google Scholar
Stellmach, S. & Hansen, U. 2004 Cartesian convection driven dynamos at low Ekman number. Phys. Rev. E 70, 056312.Google ScholarPubMed
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113 (25), 254501.CrossRefGoogle ScholarPubMed
Takahashi, F., Matsushima, M. & Honkura, Y. 2008 Scale variability in convection-driven mhd dynamos at low Ekman number. Phys. Earth Planet. Inter. 167 (3), 168–178.Google Scholar
Tilgner, A. 2012 Transitions in rapidly rotating convection driven dynamos. Phys. Rev. Lett. 109 (24), 248501.Google Scholar
Tobias, S. M., Diamond, P. H. & Hughes, D. W. 2007 𝛽-plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. J. Lett. 667 (1), L113.Google Scholar
Yadav, R. K., Gastine, T., Christensen, U. R., Duarte, L. D. V. & Reiners, A. 2016 Effect of shear and magnetic field on the heat-transfer efficiency of convection in rotating spherical shells. Geophys. J. Intl 204 (2), 1120–1133.Google Scholar
Zeldovich, Y. B. 1957 The magnetic field in the two-dimensional motion of a conducting turbulent fluid. Sov. Phys. J. Expl Theor. Phys. 4, 460–462.Google Scholar