Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T12:21:08.829Z Has data issue: false hasContentIssue false
  • English
  • Français

A lattice Boltzmann study on the drag force in bubble swarms

Published online by Cambridge University Press:  09 May 2011

J. J. J. GILLISSEN ,
S. SUNDARESAN  and
H. E. A. VAN DEN AKKER
J. J. J. GILLISSEN*
Affiliation:
Department of Multi-Scale Physics, J. M. Burgers Centre for Fluid Mechanics, Delft University of Technology, Prins Bernhardlaan 6, 2628 BW Delft, The Netherlands
S. SUNDARESAN
Affiliation:
Department of Chemical Engineering, Princeton University, Princeton, NJ 08544, USA
H. E. A. VAN DEN AKKER
Affiliation:
Department of Multi-Scale Physics, J. M. Burgers Centre for Fluid Mechanics, Delft University of Technology, Prins Bernhardlaan 6, 2628 BW Delft, The Netherlands
*
†Email address for correspondence: j.j.j.gillissen@tudelft.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

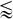Lattice Boltzmann and immersed boundary methods are used to conduct direct numerical simulations of suspensions of massless, spherical gas bubbles driven by buoyancy in a three-dimensional periodic domain. The drag coefficient CD is computed as a function of the gas volume fraction φ and the Reynolds number Re = 2RUslip/ν for 0.03 φ 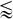0.5 and 5 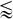Re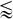 2000. Here R, Uslip and ν denote the bubble radius, the slip velocity between the liquid and the gas phases and the kinematic viscosity of the liquid phase, respectively. The results are rationalized by assuming a similarity between the CD(Reeff)-relation of the suspension and the CD(Re)-relation of an individual bubble, where the effective Reynolds number Reeff = 2RUslip/νeff is based on the effective viscosity νeff which depends on the properties of the suspension. For Re ≲ 100, we find νeff ≈ ν/(1−0.6φ1/3), which is in qualitative agreement with previous proposed correlations for CD in bubble suspensions. For Re ≳ 100, on the other hand, we find νeff ≈ RUslipφ, which is explained by considering the turbulent kinetic energy levels in the liquid phase. Based on these findings, a correlation is constructed for CD(Re, φ). A modification of the drag correlation is proposed to account for effects of bubble deformation, by the inclusion of a correction factor based on the theory of Moore (J. Fluid Mech., vol. 23, 1995, p. 749).

JFM classification

Drops and Bubbles: Bubble dynamics Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 679 , 25 July 2011 , pp. 101 - 121
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barnea, E. & Mizrahi, J. 1973 A generalized approach to the fluid dynamics of particulate systems: Part 1. general correlation for fluidization and sedimentation in solid multiparticle systems. Chem. Engng J. 5, 171–189.CrossRefGoogle Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. Phys. Rev. 94, 511.CrossRefGoogle Scholar
Blanco, A. & Magnaudet, J. 1995 The structure of the axisymmetric high-Reynolds number flow around an ellipsoidal bubble of fixed shape. Phys. Fluids 7, 1265.CrossRefGoogle Scholar
Bunner, B. & Tryggvason, G. 2003 Effect of bubble deformation on the properties of bubbly flows. J. Fluid Mech. 495, 77–118.CrossRefGoogle Scholar
Cercignani, C. 1988 The Boltzmann Equation and its Applications. Springer.Google Scholar
Chen, M., Kontomaris, K. & McLaughlin, J. B. 1998 Direct numerical simulation of droplet collisions in a turbulent channel flow. Part I: collision algorithm. Intl J. Multiphase Flow 24, 1079–1103.CrossRefGoogle Scholar
Colosqui, C. E. 2010 High-order hydrodynamics via lattice Boltzmann methods. Phys. Rev. E 81, 026702.CrossRefGoogle ScholarPubMed
Duineveld, P. C. 1995 The rise velocity and shape of bubbles in pure water at high Reynolds number. J. Fluid Mech. 292, 325–332.CrossRefGoogle Scholar
Esmaeeli, A. & Tryggvason, G. 2005 A direct numerical simulation study of the buoyant rise of bubbles at O(100) Reynolds number. Phys. Fluids 17, 093303.CrossRefGoogle Scholar
Garnier, C., Lance, M. & Marié, J. L. 2002 Measurement of local flow characteristics in buoyancy-driven bubbly flow at high void fraction. Exp. Therm. Fluid Sci. 26, 811–815.Google Scholar
Harteveld, W. K., Mudde, R. F. & Van Den Akker, H. E. A. 2003 Dynamics of a bubble column: Influence of gas distribution on coherent structures. Can. J. Chem. Engng 81, 389–394.CrossRefGoogle Scholar
He, X. & Luo, L.-S. 1997 A priori derivation of the lattice Boltzmann equation. Phys. Rev. E 55 (6/A), 6333–6336.CrossRefGoogle Scholar
Ishii, M. & Zuber, N. 1979 Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 25, 843–855.Google Scholar
Kim, J., Kim, D. & Choi, H. 2001 An immersed-boundary finite-volume method for simulations of flow in complex geometries. J. Comput Phys. 171, 132–150.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
Martínez-Mercado, J., Palacios-Morales, C. A. & Zenit, R. 2007 Measurement of pseudoturbulence intensity in monodispersed bubbly liquids for 10 < Re < 500. Phys. Fluids 19, 103302.CrossRefGoogle Scholar
Maxworthy, T., Gnann, C., Kurten, M. & Durst, F. 1996 Experiments on the rise of air bubbles in clean viscous liquids. J. Fluid Mech. 321, 421–441.Google Scholar
Mei, R. & Klausner, J. F. 1992 Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids 4, 63–70.Google Scholar
Moore, W. D. 1965 The velocity of rise of distorted gas bubbles in a liquid of small viscosity. J. Fluid Mech. 23, 749–766.CrossRefGoogle Scholar
Philippi, P. C., Hegele, L. A. Jr., dos Santos, L. O. E. & Surmas, R. 2006 From the continuous to the lattice Boltzmann equation: The discretization problem and thermal models. Phys. Rev. E 73, 056702.Google Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.CrossRefGoogle Scholar
Roma, A. M., Peskin, C. S. & Berger, M. J. 1999 An adaptive version of the immersed boundary method. J. Comput Phys. 153, 509–534.CrossRefGoogle Scholar
Sangani, A. S. & Acrivos, A. 1983 Creeping flow through cubic arrays of spherical bubbles. Intl J. Multiphase Flow 9, 181–185.Google Scholar
Sangani, A. S. & Didwania, A. K. 1993 Dynamic simulations of flows of bubbly liquids at large Reynolds numbers. J. Fluid Mech. 250, 307–337.CrossRefGoogle Scholar
Shan, X., Yuan, X.-F. & Chen, H. 2006 Kinetic theory representation of hydrodynamics: a way beyond the Navier–Stokes equation. J. Fluid Mech. 550, 413–441.CrossRefGoogle Scholar
Somers, J. A. 1993 Direct simulation of fluid flow with cellular automata and the lattice-Boltzmann equation. Appl. Sci. Res. 51 (1/2), 127.Google Scholar
Ten Cate, A., Deksen, J. J., Portela, L. M. & Van Den Akker, H. E. A. 2004 Fully resolved simulations of colliding monodisperse spheres in forced isotropic turbulence. J. Fluid Mech. 519, 233.CrossRefGoogle Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209, 448–476.Google Scholar
Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20, 053305.CrossRefGoogle Scholar
Van Sint Annaland, M., Dijkhuizen, W., Deen, N. G. & Kuipers, J. A. M. 2006 Numerical simulation of behavior of gas bubbles using a 3-D front-tracking method. AIChE J. 52, 99–110.CrossRefGoogle Scholar
Yin, X. & Koch, D. L. 2008 Lattice-Boltzmann simulation of finite Reynolds number buoyancy-driven bubbly flows in periodic and wall-bounded domains. Phys. Fluids 20, 103304.CrossRefGoogle Scholar
Zenit, R., Koch, D. L. & Sangani, A. S. 2001 Measurements of the average properties of a suspension of bubbles rising in a vertical channel. J. Fluid Mech. 429, 307–342.CrossRefGoogle Scholar