Published online by Cambridge University Press: 28 January 2021
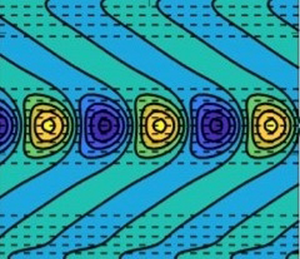
This is an ocean motivated study which investigates the impacts of sinusoidal bottom topography on baroclinic instability of zonal vertically sheared flows in the two-layer quasigeostrophic model. The corresponding linear stability problem is solved by assuming Fourier-mode solutions in both the zonal and meridional directions. In the presence of variable topographic features, the Fourier modes become coupled due to phase shifts in the wavevectors. The spectral discretisation method used in this work retains the primary relationship between different Fourier modes; thus, the linear stability eigenproblem can be solved for any periodic topography. Moreover, this method does not need any additional assumptions, such as considering small-amplitude or large-scale bottom irregularities, as in some previous studies. In this work, the eigenproblem is solved for a range of topographic amplitudes and wavenumbers, and their effects on the growth rates and shapes of the most unstable eigenmodes are discussed. In general, both the zonal and meridional variations in topography tend to suppress the baroclinic instability. However, it is found that only meridionally varying topography affects the magnitudes of the fastest growth rates. In this instance, unstable modes appear to form two clusters well separated in the zonal wavenumber axis and growth rate maxima occur at two distinct zonal wavenumbers. Dependencies of the characteristics of these clusters on the values of topography amplitude and ridge width are reviewed. Finally, doubly periodic numerical simulations are used to verify the results from the linear stability analysis.