Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T06:44:14.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Mass transfer around bubbles flowing in cylindrical microchannels

Published online by Cambridge University Press:  23 April 2019

Javier Rivero-Rodriguez Open the ORCID record for Javier Rivero-Rodriguez [Opens in a new window]  and
Benoit Scheid Open the ORCID record for Benoit Scheid [Opens in a new window]
Javier Rivero-Rodriguez*
Affiliation:
TIPs, Université Libre de Bruxelles, C.P. 165/67, Avenue F. D. Roosevelt 50, 1050 Bruxelles, Belgium
Benoit Scheid
Affiliation:
TIPs, Université Libre de Bruxelles, C.P. 165/67, Avenue F. D. Roosevelt 50, 1050 Bruxelles, Belgium
*
†Email address for correspondence: jriveror@ulb.ac.be
Get access Rights & Permissions [Opens in a new window]

Abstract

This work focuses on the mass transfer around unconfined bubbles in cylindrical microchannels when they are arranged in a train. We characterise how the mass transfer, quantified by the Sherwood number, 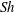$Sh$, is affected by the channel and bubble sizes, distance between bubbles, diffusivity, mean flow velocity, deformation of the bubble, the presence of surfactants in the limit of rigid interface and off-centred positions of the bubbles. We analyse the influence of the dimensionless numbers and especially the distance between bubbles and the Péclet number, 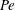$Pe$, which we vary over eight decades, identifying five different mass transfer regimes. We show different concentration patterns and the dependence of the Sherwood numbers. These regimes can be classified by either the importance of the diffusion along the streamlines or the interaction between bubbles. For small 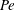$Pe$ the diffusion along the streamlines is not negligible as compared to convection, whereas for large 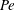$Pe$ convection dominates in the streamlines direction and, thus, crosswind diffusion becomes crucial in governing the mass transfer through boundary layers or the remaining wake behind the bubbles. Interaction of bubbles occurs for very small 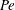$Pe$ where the mass transfer is purely diffusive, or for very large 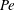$Pe$ where long wakes eventually reach the following bubble. We also observe that the bubble deformability mainly affects the 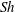$Sh$ in the regime for very large 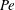$Pe$ in which bubbles interaction matters, and also that the rigid interface affects the boundary layer and the remaining wake. The effect of off-centred position of the bubble, determined by the transverse force balance, is also limited to large 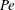$Pe$. The boundary layers on rigid bubble surfaces are thicker than those on stress-free bubble surfaces, and thus the mass transfer is weaker. For centred bubbles, the influence of inertia on the mass transfer is negligible. Finally, we discuss the implication of our results on the dissolution of bubbles.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow Micro-/Nano-fluid dynamics: Microfluidics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 110 - 142
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abiev, R. S. 2013 Bubbles velocity, Taylor circulation rate and mass transfer model for slug flow in milli-and microchannels. Chem. Engng J. 227, 66–79.Google Scholar
Atasi, O., Haut, B., Pedrono, A., Scheid, B. & Legendre, D. 2018 Influence of soluble surfactants and deformation on the dynamics of centered bubbles in cylindrical microchannels. Langmuir 34 (34), 10048–10062.Google Scholar
Auguste, F. & Magnaudet, J. 2018 Path oscillations and enhanced drag of light rising spheres. J. Fluid Mech. 841, 228–266.Google Scholar
Barak, M. & Katz, Y. 2005 Microbubbles. Chest 128 (4), 2918–2932.Google Scholar
Beltramo, P. J., Gupta, M., Alicke, A., Liascukiene, I., Gunes, D. Z., Baroud, C. N. & Vermant, J. 2017 Arresting dissolution by interfacial rheology design. Proc. Natl Acad. Sci. USA 114 (39), 10373–10378.Google Scholar
Chi, J. J., Johnstone, T. C., Voicu, D., Mehlmann, P., Dielmann, F., Kumacheva, E. & Stephan, D. W. 2017 Quantifying the efficiency of CO2 capture by Lewis pairs. Chem. Sci. 8 (4), 3270–3275.Google Scholar
Clift, R. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Cubaud, T. & Ho, C.-M. 2004 Transport of bubbles in square microchannels. Phys. Fluids 16 (12), 4575–4585.Google Scholar
Cubaud, T., Sauzade, M. & Sun, R. 2012 Co2 dissolution in water using long serpentine microchannels. Biomicrofluidics 6 (2), 022002.Google Scholar
Deckwer, W.-D. 1980 On the mechanism of heat transfer in bubble column reactors. Chem. Engng Sci. 35 (6), 1341–1346.Google Scholar
Dhotre, M. T. & Joshi, J. B. 2004 Two-dimensional CFD model for the prediction of flow pattern, pressure drop and heat transfer coefficient in bubble column reactors. Chem. Engng Res. Design 82 (6), 689–707.Google Scholar
Durgadevi, A. & Pushpavanam, S. 2018 An experimental and theoretical investigation of pure carbon dioxide absorption in aqueous sodium hydroxide in glass millichannels. J. CO2 Utilization 26, 133–142.Google Scholar
Gallino, G., Gallaire, F., Lauga, E. & Michelin, S. 2018 Physics of bubble-propelled microrockets. Adv. Funct. Mater. 28 (25), 1800686.Google Scholar
Ganapathy, H., Shooshtari, A., Dessiatoun, S., Alshehhi, M. & Ohadi, M. 2014 Fluid flow and mass transfer characteristics of enhanced CO2 capture in a minichannel reactor. Appl. Energy 119, 43–56.Google Scholar
Gekle, S. 2017 Dispersion of solute released from a sphere flowing in a microchannel. J. Fluid Mech. 819, 104–120.Google Scholar
Griffith, R. M. 1960 Mass transfer from drops and bubbles. Chem. Engng Sci. 12 (3), 198–213.Google Scholar
Haas, U., Schmidt-Traub, H. & Brauer, H. 1972 Umströmung kugelförmiger blasen mit innerer zirkulation. Chemie Ingenieur Technik 44 (18), 1060–1068.Google Scholar
Hashemi, S. M. H., Modestino, M. A. & Psaltis, D. 2015 A membrane-less electrolyzer for hydrogen production across the pH scale. Energy Environ. Sci. 8 (7), 2003–2009.Google Scholar
Hung, L.-H., Teh, S.-Y., Jester, J. & Lee, A. P. 2010 PLGA micro/nanosphere synthesis by droplet microfluidic solvent evaporation and extraction approaches. Lab on a Chip 10 (14), 1820–1825.Google Scholar
Hyman, W. A. & Skalak, R. 1972 Viscous flow of a suspension of liquid drops in a cylindrical tube. Appl. Sci. Res. 26 (1), 27–52.Google Scholar
Kandlikar, S., Garimella, S., Li, D., Colin, S. & King, M. R. 2005 Heat Transfer and Fluid Flow in Minichannels and Microchannels. Elsevier.Google Scholar
Kashid, M. N., Renken, A. & Kiwi-Minsker, L. 2011 Gas–liquid and liquid–liquid mass transfer in microstructured reactors. Chem. Engng Sci. 66 (17), 3876–3897.Google Scholar
Kuo, J. S. & Chiu, D. T. 2011 Controlling mass transport in microfluidic devices. Annu. Rev. Anal. Chem. 4, 275–296.Google Scholar
Mehta, G., Mehta, K., Sud, D., Song, J. W., Bersano-Begey, T., Futai, N., Heo, Y. S., Mycek, M.-A., Linderman, J. J. & Takayama, S. 2007 Quantitative measurement and control of oxygen levels in microfluidic poly (dimethylsiloxane) bioreactors during cell culture. Biomed. Microdevices 9 (2), 123–134.Google Scholar
Michelin, S., Guérin, E. & Lauga, E. 2018 Collective dissolution of microbubbles. Phys. Rev. Fluids 3 (4), 043601.Google Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23 (10), 101901.Google Scholar
Mikaelian, D., Haut, B. & Scheid, B. 2015a Bubbly flow and gas–liquid mass transfer in square and circular microchannels for stress-free and rigid interfaces: CFD analysis. Microfluid Nanofluid 19 (3), 523–545.Google Scholar
Mikaelian, D., Haut, B. & Scheid, B. 2015b Bubbly flow and gas–liquid mass transfer in square and circular microchannels for stress-free and rigid interfaces: dissolution model. Microfluid Nanofluid 19 (4), 899–911.Google Scholar
Riechers, B., Maes, F., Akoury, E., Semin, B., Gruner, P. & Baret, J.-C. 2016 Surfactant adsorption kinetics in microfluidics. Proc. Natl Acad. Sci. USA 113 (41), 11465–11470.Google Scholar
Rivero-Rodriguez, J., Perez-Saborid, M. & Scheid, B.2018 PDEs on deformable domains: boundary arbitrary Lagrangian–Eulerian and deformable boundary perturbation methods. J. Comput. Meth. Appl. Mech. Engng (submitted) arXiv:1810.10001.Google Scholar
Rivero-Rodriguez, J. & Scheid, B. 2018a Bubble dynamics in microchannels: inertial and capillary migration forces. J. Fluid Mech. 842, 215–247.Google Scholar
Rivero-Rodriguez, J. & Scheid, B. 2018b Bubble dynamics in microchannels: inertial and capillary migration forces. J. Fluid Mech. 855, 1242–1245.Google Scholar
Rohsenow, W. M., Hartnett, J. P. & Ganic, E. N 1985 Handbook of Heat Transfer Fundamentals. p. 1440. McGraw-Hill.Google Scholar
Segré, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow part 2. Experimental results and interpretation. J. Fluid Mech. 14 (1), 136–157.Google Scholar
Shim, S., Wan, J., Hilgenfeldt, S., Panchal, P. D. & Stone, H. A. 2014 Dissolution without disappearing: multicomponent gas exchange for CO2 bubbles in a microfluidic channel. Lab on a Chip 14 (14), 2428–2436.Google Scholar
Squires, T. M., Messinger, R. J. & Manalis, S. R. 2008 Making it stick: convection, reaction and diffusion in surface-based biosensors. Nature Biotechnol. 26 (4), 417.Google Scholar
Taylor, T. D. 1963 Heat transfer from single spheres in a low Reynolds number slip flow. Phys. Fluids 6 (7), 987–992.Google Scholar
Vadapalli, A., Goldman, D. & Popel, A. S. 2002 Calculations of oxygen transport by red blood cells and hemoglobin solutions in capillaries. Artif. Cells Blood Substitutes Biotechnol. 30 (3), 157–188.Google Scholar
Westerwalbesloh, C., Grünberger, A., Stute, B., Weber, S., Wiechert, W., Kohlheyer, D. & von Lieres, E. 2015 Modeling and CFD simulation of nutrient distribution in picoliter bioreactors for bacterial growth studies on single-cell level. Lab on a Chip 15 (21), 4177–4186.Google Scholar
Xu, J. H., Tan, J., Li, S. W. & Luo, G. S. 2008 Enhancement of mass transfer performance of liquid–liquid system by droplet flow in microchannels. Chem. Engng J. 141 (1–3), 242–249.Google Scholar