Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T12:10:33.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-equilibrium thermal transport and entropy analyses in rarefied cavity flows

Published online by Cambridge University Press:  14 February 2019

Vishnu Venugopal ,
Divya Sri Praturi Open the ORCID record for Divya Sri Praturi [Opens in a new window]  and
Sharath S. Girimaji
Vishnu Venugopal
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA
Divya Sri Praturi*
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA
Sharath S. Girimaji
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA Ocean Engineering Department, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: divya249@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Thermal transport in rarefied flows far removed from thermodynamic equilibrium is investigated using kinetic-theory-based numerical simulations. Two numerical schemes – unified gas kinetic scheme (UGKS) and direct simulation Monte Carlo (DSMC) – are employed to simulate transport at different degrees of rarefaction. Lid-driven cavity flow simulations of argon gas are performed over a range of Knudsen numbers, Mach numbers and cavity shapes. Thermal transport is then characterized as a function of lid Mach number and Knudsen number for different cavity shapes. Vast deviations from the Fourier law – including thermal transport aligned along the direction of temperature gradient – are observed. 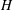Entropy implications are examined using Sackur–Tetrode and Boltzmann $H$-theorem formulations. At low Knudsen and Mach numbers, thermal transport is shown to be amenable to both entropy formulations. However, beyond moderate Knudsen and Mach numbers, thermal transport complies only with the Boltzmann 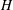$H$-theorem entropy statement. Two extended thermodynamic models are compared against simulation data and found to account for some of the observed non-equilibrium behaviour.

JFM classification

Rarefied Gas Flow: Kinetic theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 995 - 1025
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, R. K. & Balakrishnan, R.1996 Numerical simulation of BGK-Burnett equations. Tech. Rep. DTIC Document.Google Scholar
Agarwal, R. K., Yun, K.-Y. & Balakrishnan, R. 2001 Beyond Navier–Stokes: Burnett equations for flows in the continuum–transition regime. Phys. Fluids 13 (10), 3061–3085.Google Scholar
Aristov, V. V. 1998 A steady state, supersonic flow solution of the Boltzmann equation. Phys. Lett. A 250 (4–6), 354–359.Google Scholar
Aristov, V. V., Frolova, A. A. & Zabelok, S. A. 2009 A new effect of the nongradient transport in relaxation zones. Europhys. Lett. 88 (3), 30012.Google Scholar
Aristov, V. V., Frolova, A. A. & Zabelok, S. A. 2012 Supersonic flows with nontraditional transport described by kinetic methods. Commun. Comput. Phys. 11 (4), 1334–1346.Google Scholar
Bertin, J. J. & Cummings, R. M. 2006 Critical hypersonic aerothermodynamic phenomena*. Annu. Rev. Fluid Mech. 38, 129–157.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. i. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.Google Scholar
Bird, G. A. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon.Google Scholar
Bobylev, A. V. 1982 The Chapman-Enskog and Grad methods for solving the Boltzmann equation. Akad. Nauk SSSR Dokl. 262, 71–75.Google Scholar
Burnett, D. 1936 The distribution of molecular velocities and the mean motion in a non-uniform gas. Proc. Lond. Math. Soc. 2 (1), 382–435.Google Scholar
Chang, W. & Uhlenbeck, G. E.1948 On the transport phenomena in rarefied gases. Tech. Rep. DTIC Document.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases. Cambridge University Press.Google Scholar
Guo, Z., Xu, K. & Wang, R. 2013 Discrete unified gas kinetic scheme for all Knudsen number flows: low-speed isothermal case. Phys. Rev. E 88 (3), 033305.Google Scholar
Huang, J.-C., Xu, K. & Yu, P. 2012 A unified gas-kinetic scheme for continuum and rarefied flows II: multi-dimensional cases. Commun. Comput. Phys. 3 (3), 662–690.Google Scholar
Huang, J.-C., Xu, K. & Yu, P. 2013 A unified gas-kinetic scheme for continuum and rarefied flows III: microflow simulations. Commun. Comput. Phys. 14 (5), 1147–1173.Google Scholar
Ilyin, O. 2017 Anomalous heat transfer for an open non-equilibrium gaseous system. J. Stat. Mech. 2017 (5), 053201.Google Scholar
Kerimo, J. & Girimaji, S. S. 2007 Boltzmann–BGK approach to simulating weakly compressible 3D turbulence: comparison between lattice Boltzmann and gas kinetic methods. J. Turbul. 8, 46.Google Scholar
Kumar, G., Girimaji, S. S. & Kerimo, J. 2013 Weno-enhanced gas-kinetic scheme for direct simulations of compressible transition and turbulence. J. Comput. Phys. 234, 499–523.Google Scholar
May, G., Srinivasan, B. & Jameson, A. 2007 An improved gas-kinetic BGK finite-volume method for three-dimensional transonic flow. J. Comput. Phys. 220 (2), 856–878.Google Scholar
Mohammadzadeh, A., Roohi, E., Niazmand, H., Stefanov, S. & Myong, R. S. 2012 Thermal and second-law analysis of a micro-or nanocavity using direct-simulation Monte Carlo. Phys. Rev. E 85 (5), 056310.Google Scholar
Prendergast, K. H. & Xu, K. 1993 Numerical hydrodynamics from gas-kinetic theory. J. Comput. Phys. 109 (1), 53–66.Google Scholar
Sackur, O. 1911 Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme. Ann. Phys. 341 (15), 958–980.Google Scholar
Shakhov, E. M. 1968 Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 3 (5), 95–96.Google Scholar
Shizgal, B. 1981 A Gaussian quadrature procedure for use in the solution of the Boltzmann equation and related problems. J. Comput. Phys. 41 (2), 309–328.Google Scholar
Tetrode, H. von 1912 Die chemische Konstante der Gase und das elementare Wirkungsquantum. Ann. Phys. 343 (7), 434–442.Google Scholar
Venugopal, V.2016 Rarefaction effects on thermal and mass transport in cavity flows. PhD thesis, Texas A&M University.Google Scholar
Venugopal, V. & Girimaji, S. S. 2015 Unified gas kinetic scheme and direct simulation monte carlo computations of high-speed lid-driven microcavity flows. Commun. Comput. Phys. 17 (05), 1127–1150.Google Scholar
Xu, K. 2001 A gas-kinetic BGK scheme for the Navier–Stokes equations and its connection with artificial dissipation and Godunov method. J. Comput. Phys. 171 (1), 289–335.Google Scholar
Xu, K. & He, X. 2003 Lattice Boltzmann method and gas-kinetic BGK scheme in the low-Mach number viscous flow simulations. J. Comput. Phys. 190 (1), 100–117.Google Scholar
Xu, K. & Huang, J.-C. 2010 A unified gas-kinetic scheme for continuum and rarefied flows. J. Comput. Phys. 229 (20), 7747–7764.Google Scholar
Xu, K., Mao, M. & Tang, L. 2005 A multidimensional gas-kinetic BGK scheme for hypersonic viscous flow. J. Comput. Phys. 203 (2), 405–421.Google Scholar
Yun, K.-Y., Agarwal, R. K., Balakrishnan, R., Yun, K.-Y., Agarwal, R. & Balakrishnan, R. 1997 A comparative study of augmented Burnett and BGK-Burnett equations for computing hypersonic blunt body flows. In AIAA, Aerospace Sciences Meeting & Exhibit, 35 th, Reno, NV.Google Scholar
Zhong, X. 1991 Development and Computation of Continuum Higher Order Constitutive Relations for High-altitude Hypersonic Flow. Stanford University.Google Scholar
Zhu, Y., Zhong, C. & Xu, K. 2017 Unified gas-kinetic scheme with multigrid convergence for rarefied flow study. Phys. Fluids 29 (9), 096102.Google Scholar