Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T05:30:30.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear evolution of a baroclinic wave and imbalanced dissipation

Published online by Cambridge University Press:  09 September 2014

Balasubramanya T. Nadiga
Balasubramanya T. Nadiga*
Affiliation:
Los Alamos National Laboratory, MS-B214, Los Alamos, NM 87545, USA
*
†Email address for correspondence: balu@lanl.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the nonlinear evolution of an unstable baroclinic wave in a regime of rotating stratified flow that is of relevance to interior circulation in the oceans and in the atmosphere: a regime characterized by small large-scale Rossby and Froude numbers, a small vertical to horizontal aspect ratio and no bounding horizontal surfaces. Using high-resolution simulations of the non-hydrostatic Boussinesq equations and companion integrations of the balanced quasi-geostrophic (QG) equations, we present evidence for a local route to dissipation of balanced energy directly through interior turbulent cascades. That is, analysis of simulations presented in this study suggest that a developing baroclinic instability can lead to secondary instabilities that can cascade a small fraction of the energy forward to unbalanced scales whereas the bulk of the energy is confined to large balanced scales. Mesoscale shear and strain resulting from the hydrostatic geostrophic baroclinic instability drive frontogenesis. The fronts in turn support ageostrophic secondary circulation and instabilities. These two processes acting together lead to a quick rise in dissipation rate which then reaches a peak and begins to fall slowly when frontogenesis slows down; eventually balanced and imbalanced modes decouple. A measurement of the dissipation of balanced energy by imbalanced processes reveals that it scales exponentially with Rossby number of the base flow. We expect that this scaling will hold more generally than for the specific set-up we consider given the fundamental nature of the dynamics involved. In other results, (a) a break is seen in the total energy (TE) spectrum at small scales: while a steep 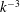$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k^{-3}$ geostrophic scaling (where 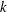$k$ is the three-dimensional wavenumber) is seen at intermediate scales, the smaller scales display a shallower 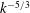$k^{-5/3}$ scaling, reminiscent of the atmospheric spectra of Nastrom & Gage and (b) at the higher of the Rossby numbers considered a minimum is seen in the vertical shear spectrum, reminiscent of similar spectra obtained using in situ measurements.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 965 - 1006
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. & Hoskins, B. J. 1978 Energy spectra predicted by semi-geostrophic theories of frontogenesis. J. Atmos. Sci. 35 (3), 509–512.Google Scholar
Babin, A., Mahalov, A., Nicolaenko, B. & Zhou, Y. 1997 On the asymptotic regimes and the strongly stratified limit of rotating Boussinesq equations. Theor. Comput. Fluid Dyn. 9 (3–4), 223–251.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Bartello, P. 2010 Quasigeostrophic and stratified turbulence in the atmosphere. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans, pp. 117–130. Springer.Google Scholar
Bouchut, F., Ribstein, B. & Zeitlin, V. 2011 Inertial, barotropic, and baroclinic instabilities of the Bickley jet in two-layer rotating shallow water model. Phys. Fluids 23 (12), 126601.Google Scholar
Boyd, J. P. 1992 The energy spectrum of fronts: time evolution of shocks in Burgers’ equation. J. Atmos. Sci. 49 (2), 128–139.2.0.CO;2>CrossRefGoogle Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.2.0.CO;2>CrossRefGoogle Scholar
Chasnov, J. R. 1994 Similarity states of passive scalar transport in isotropic turbulence. Phys. Fluids 6, 1036–1051.Google Scholar
Danioux, E., Vanneste, J., Klein, P. & Sasaki, H. 2012 Spontaneous inertia-gravity-wave generation by surface-intensified turbulence. J. Fluid Mech. 699, 153–173.CrossRefGoogle Scholar
Ferrari, R. & Wunsch, C. 2008 Ocean circulation kinetic energy: reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 41 (1), 253–282.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Fu, L.-L. & Flierl, G. R. 1980 Nonlinear energy and enstrophy transfers in a realistically stratified ocean. Dyn. Atmos. Oceans 4 (4), 219–246.CrossRefGoogle Scholar
Gargett, A. E., Hendricks, P. J., Sanford, T. B., Osborn, T. R. & Williams, A. J. 1981 A composite spectrum of vertical shear in the upper ocean. J. Phys. Oceanogr. 11 (9), 1258–1271.Google Scholar
Gent, P. R. & McWilliams, J. C. 1990 Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 20 (1), 150–155.2.0.CO;2>CrossRefGoogle Scholar
Gill, A. E. 1982 Atmosphere–Ocean Dynamics. p. 662. Academic Press.Google Scholar
Holton, J. 2004 An Introduction to Dynamic Meteorology, 4th edn Academic Press.Google Scholar
Hoskins, B. J. 1974 The role of potential vorticity in symmetric stability and instability. Q. J. R. Meteorol. Soc. 100 (425), 480–482.CrossRefGoogle Scholar
Hoskins, B. J., Draghici, I. & Davies, H. C. 1978 A new look at the $\omega $ -equation. Q. J. R. Meteorol. Soc. 104 (439), 31–38.Google Scholar
Lesieur, M. 1997 Turbulence in Fluids. Kluwer.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Lindzen, R. S. & Fox-Rabinovitz, M. 1989 Consistent vertical and horizontal resolution. Mon. Weath. Rev. 117 (11), 2575–2583.2.0.CO;2>CrossRefGoogle Scholar
McWilliams, J. C. 1985 A uniformly valid model spanning the regimes of geostrophic and isotropic, stratified turbulence: balanced turbulence. J. Atmos. Sci. 42 (16), 1773–1774.2.0.CO;2>CrossRefGoogle Scholar
McWilliams, J. C. 2006 Fundamentals of Geophysical Fluid Dynamics. Cambridge University Press.Google Scholar
McWilliams, J. C., Yavneh, I., Cullen, M. J. P. & Gent, P. R. 1998 The breakdown of large-scale flows in rotating, stratified fluids. Phys. Fluids 10, 3178–3184.CrossRefGoogle Scholar
Molemaker, M. J., McWilliams, J. C. & Capet, X. 2010 Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 654, 35–63.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2005 Baroclinic instability and loss of balance. J. Phys. Oceanogr. 35, 1505–1517.CrossRefGoogle Scholar
Nadiga, B. T. & Straub, D. N. 2010 Alternating zonal jets and energy fluxes in barotropic wind-driven gyres. Ocean Model. 33 (3), 257–269.CrossRefGoogle Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 49 (9), 950–960.2.0.CO;2>CrossRefGoogle Scholar
Plougonven, R. & Snyder, C. 2007 Inertia-gravity waves spontaneously generated by jets and fronts. Part I: different baroclinic life cycles. J. Atmos. Sci. 64 (7), 2502–2520.CrossRefGoogle Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21 (10), 106601.Google Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65 (7), 2416–2424.CrossRefGoogle Scholar
Simon, G. & Nadiga, B. T.2014 Baroclinic instability in a triply periodic domain. Preprint.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.CrossRefGoogle Scholar
Snyder, C., Skamarock, W. C. & Rotunno, R. 1993 Frontal dynamics near and following frontal collapse. J. Atmos. Sci. 50 (18), 3194–3212.Google Scholar
Straub, D. N. & Nadiga, B. T. 2014 Energy fluxes in the quasigeostrophic double Gyre problem. J. Phys. Oceanogr 44, 1505–1522.Google Scholar
Taylor, M. A., Kurien, S. & Eyink, G. L. 2003 Recovering isotropic statistics in turbulence simulations: the Kolmogorov 4/5th law. Phys. Rev. E 68 (2), 026310.Google Scholar
Thomas, L. N., Tandon, A. & Mahadevan, A. 2008 Submesoscale processes and dynamics. In Ocean Modeling in An Eddying Regime (ed. Hecht, M. W. & Hasumi, H.), vol. 177, pp. 17–38. American Geophysical Union.Google Scholar
Thomas, L. N., Taylor, J. R., Ferrari, R. & Joyce, T. M. 2013 Symmetric instability in the gulf stream. Deep-Sea Res. II 91, 96–110.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Viúdez, Á. & Dritschel, D. G. 2004 Optimal potential vorticity balance of geophysical flows. J. Fluid Mech. 521 (1), 343–352.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar