Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T20:44:45.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal forces exerted upon a long cylinder oscillating in an axial flow

Published online by Cambridge University Press:  11 July 2014

L. Divaret ,
O. Cadot ,
P. Moussou  and
O. Doaré
L. Divaret*
Affiliation:
Unité de Mécanique, Ecole Nationale Supérieure de Techniques Avancées, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France LaMSID, UMR CNRS/EDF/CEA 2832, 1 Avenue du Général de Gaulle, 92140 Clamart, France
O. Cadot
Affiliation:
Unité de Mécanique, Ecole Nationale Supérieure de Techniques Avancées, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France
P. Moussou
Affiliation:
LaMSID, UMR CNRS/EDF/CEA 2832, 1 Avenue du Général de Gaulle, 92140 Clamart, France
O. Doaré
Affiliation:
Unité de Mécanique, Ecole Nationale Supérieure de Techniques Avancées, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France
*
†Email address for correspondence: lise.divaret@edf.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

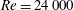This work aims to improve understanding of the damping induced by an axial flow on a rigid cylinder undergoing small lateral oscillations within the framework of the quasistatic assumption. The study focuses on the normal force exerted on the cylinder for a Reynolds number of $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=24\, 000$ (based on the cylinder diameter and axial flow velocity). Both dynamic and static approaches are investigated. With the static approach, fluid forces, pressure distributions and velocity fields are measured for different yaw angles and cylinder lengths in a wind tunnel. It is found that for yaw angles smaller than 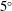$5{^\circ }$, the normal force varies linearly with the angle and is fully dominated by its lift component. The lift originates from the high pressure coefficient at the front of the cylinder, which is found to depend linearly on the angle, and from a base pressure coefficient that remains close to zero independent of the yaw angle. At the base, a flow deficit and two counter-rotating vortices are observed. A numerical simulation using a 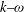$k\mbox{--}\omega $ shear stress transport turbulence model confirms the static experimental results. A dynamic experiment conducted in a water tunnel brings out damping-rate values during free oscillations of the cylinder. As expected from the linear dependence of the normal force on the yaw angle observed with the static approach, the damping rate increases linearly with the axial flow velocity. Satisfactory agreement is found between the two approaches.

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 649 - 669
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archambeau, F., Sakiz, M. & Namane, M. 2004 Code saturne: a finite volume code for turbulent flows. Intl J. Fin. 1 (1), 1–62.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration. Van Nostrand Reinhold.Google Scholar
Bursnall, W. J. & Loftin, L. K.1951 Experimental investigation of the pressure distribution about a yawed circular cylinder in the critical Reynolds number range. Tech. Rep. 2463. National Advisory Committee for Aeronautics.Google Scholar
Chen, S. 1987 Flow-induced Vibration of Circular Cylindrical Structures. Hemisphere Publishing Corporation.Google Scholar
Ersdal, S. & Faltinsen, O. M. 2006 Normal forces on cylinders in near-axial flow. J. Fluids Struct. 22 (8), 1057–1077.CrossRefGoogle Scholar
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Intl J. Numer. Meth. Engng 77 (11), 1309–1331.Google Scholar
Gosselin, F. P. & de Langre, E. 2011 Drag reduction by reconfiguration of a poroelastic system. J. Fluids Struct. 27 (7), 1111–1123.Google Scholar
Guo, C. Q. & Paidoussis, M. P. 2000 Stability of rectangular plates with free side-edges in two-dimensional inviscid channel flow. Trans. ASME J. Appl. Mech. 67 (1), 171–176.CrossRefGoogle Scholar
Hoerner, S. F. 1965 Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance. Hoerner Fluid Dynamics.Google Scholar
Hoerner, S. F. 1985 Fluid-Dynamic Lift: Practical Information on Aerodynamic and Hydrodynamic Lift. Hoerner Fluid Dynamics.Google Scholar
Jones, R. T.1947 Effects of sweepback on boundary layer and separation. Tech. Rep. 884. National Advisory Committee for Aeronautics.Google Scholar
de Langre, E., Païdoussis, M. P., Doaré, O. & Modarres-Sadeghi, Y. 2007 Flutter of long flexible cylinders in axial flow. J. Fluid Mech. 571, 371–389.Google Scholar
Lighthill, M. J. 1960 Note on the swimming of slender fish. J. Fluid Mech. 9, 305–317.CrossRefGoogle Scholar
Menter, F. R.1993 Zonal two equation k- $\omega $ turbulence models for aerodynamic flows. Tech. Rep. AIAA 93-2906. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Menter, F. R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605.Google Scholar
Morison, J. R. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. Petrol. Trans. AIME 189, 149–154.Google Scholar
Ortloff, C. R. & Ives, J. 1969 On the dynamic motion of a thin flexible cylinder in a viscous stream. J. Fluid Mech. 38, 713–720.Google Scholar
Païdoussis, M. P. 2004 Fluid-Structure Interactions: Slender Structures and Axial Flow, vol. 2. Academic Press, chap. 8 and Appendix Q.Google Scholar
Païdoussis, M. P., Price, S. J. & de Langre, E. 2011 Fluid-Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Ramberg, S. E. 1983 The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders. J. Fluid Mech. 128, 81–107.Google Scholar
Relf, E. H. & Powell, C. H.1917 Tests on smooth and stranded wires inclined to the wind direction and a comparison of the results on stranded wires in air and water. Tech. Rep. Reports and Memoranda 307. Aeronautical Research Committee, London.Google Scholar
De Ridder, J., Degroote, J., Van Tichelen, K., Schuurmans, P. & Vierendeels, J. 2013 Modal characteristics of a flexible cylinder in turbulent axial flow from numerical simulations. J. Fluids Struct. 43, 110–123.Google Scholar
Sears, W. R. 1948 The boundary layer of yawed cylinders. J. Aeronaut. Sci. 15 (1), 49–52.Google Scholar
Smith, R. A., Kao, T. W. & Moon, W. T. 1971 Experiments on the flow about a yawed circular cylinder. Trans. ASME J. Basic Engng 94 (4), 771–776.Google Scholar
Taylor, G. 1952 Analysis of the swimming of long and narrow animals. Proc. R. Soc. Lond. 214, 158–183.Google Scholar
Zdravkovich, M. M. 2003 Flow Around Circular Cylinders. Volume 2: Applications. Oxford University Press.CrossRefGoogle Scholar